私がアルゴリズムの勉強を始めてから、最初にぶつかった壁は動的計画法(DP)でした。
動的計画法を用いて、部分和問題を解く方法を解説します。
1. 部分和問題:重さの和をxにできるか判定する
問題
\(1~n\) の番号が付いたn個のおもりがあり、おもり \(i\) の重さは \(a_i\) です。
引用元:https://paiza.jp/works/mondai/dp_primer/dp_primer_partial_sums_step0
おもりを何個か選んで重さの和がxとなるようにすることができるかどうか判定してください。なお、同じおもりを2個以上選ぶことはできません。
方針
「ある重さ j 」を
「 i 番目のおもりを選ぶことで実現できるか否か」という状態を記録していきます。
道的計画法による部分和問題の解法は、言葉ではこのように表現することができます。
つまり、まず
「1番目のおもりを選ぶことで、重さ \(j\) (\(0\le j\le x\)) を実現できるか否か」
を、それぞれの \(j\)(\(j = 0, 1, 2, … x\)) について調べます。
この情報を用いて、
「2番目のおもりを選ぶことで、重さ \(j\) (\(0\le j\le x\)) を実現できるか否か」
を、それぞれの \(j\) (\(j = 0, 1, 2, … x\)) について調べます。
このように、\(i\) 番目 (\(i = 1, 2, … n\)) のおもりに対して、同様の調査をします。
以上より、計算量は \(O(x\times n)\) となることが分かります。
ちなみに、これ以降の問題はすべて(最終問題は少し工夫が必要)、この問題の考え方とほとんど同じ解き方です。よって、まず本問を深く理解することは重要です。
具体例で考える
\(n = 5, x = 19\)
\(a_1 = 7, a_2 = 18, a_3 = 5, a_4 = 4, a_5 = 8\)
の場合を考えます。
下の表をご覧ください。縦軸が \(i\) , 横軸が \(j\) です。
まず「 \(a_1=7\) のおもりを選ぶことで、重さ \(j\) (\(0\le j\le x\)) を実現できるか否か」を考えます。
\(True = 1, False = 0\) とすると、表の1列目を次のように埋めることができます。
重さ7のおもりを用いて実現できる重さは、0(おもりを選ばない)と7(おもりを選ぶ)です。
ここで注意点があります。「なお、同じおもりを2個以上選ぶことはできません。」という制約があるため、例えば重さ7のおもりを2つ選んだことにして、重さ14を実現することはできません。
同じ重さのおもりを無制限に選べるパターンの問題は、本記事の最後に紹介します。
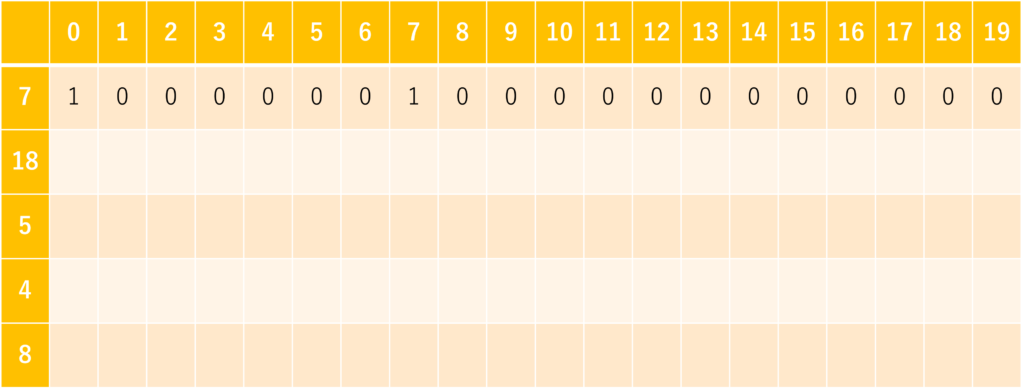
次に、2つ目のおもりについて考えます。
重さ18のおもりを選んで実現できる重さは、18だけです。
ここで注意したいのは、
\(i\) 番目のおもり(の行)について考えるとき、\(i-1\) 行目の情報を用いるということです。
すなわち、先ほど考えた1行目の情報を踏まえて、「2番目の(重さ18の)おもりを選んで実現できる重さ」の情報を付加していきます。
よって、\(j=0\) の列、\(j=7\) の列は、1行目の値をそのまま下に降ろすような形になります。
\(j=18\) の列では、\(j – a_i = 18 – 18 = 0\) →\(i = 1, j = 0\) の列を参照すれば、\(i=2, j=18\) を実現できるか否かが判別できます。
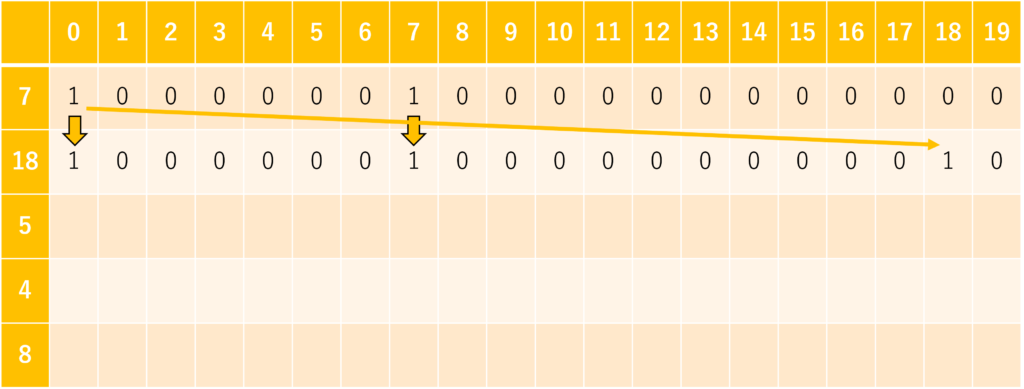
3番目のおもりについても考えます。今、\(i = 3\) であるから \(i-1=2\) 行目を参照します。
\(j=5\) を実現できることはすぐにわかります。また、2行目の \(j=7\) の列を参照すると、\(j=12\) も実現できることが分かります。
ここまでの議論で、何となく流れは分かってくると思います。初めは慣れない考え方ですが、具体的な数値の例を使い、自分で表を書いてみると理解が深まります。
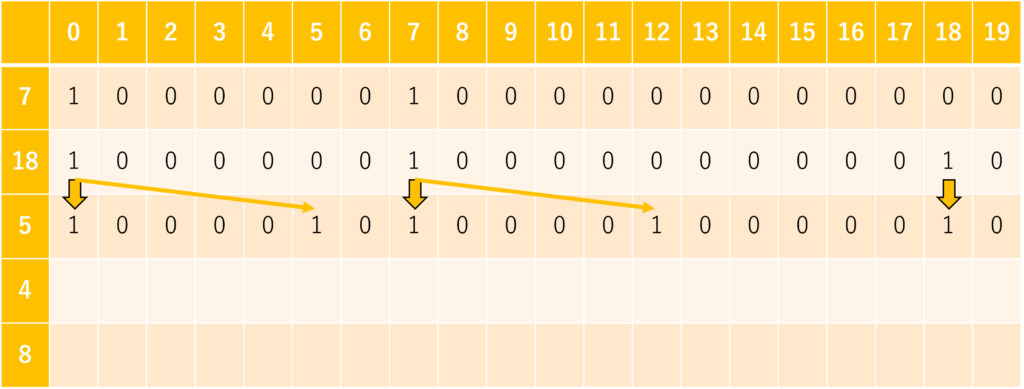
4番目のおもり(\(i = 4\))について
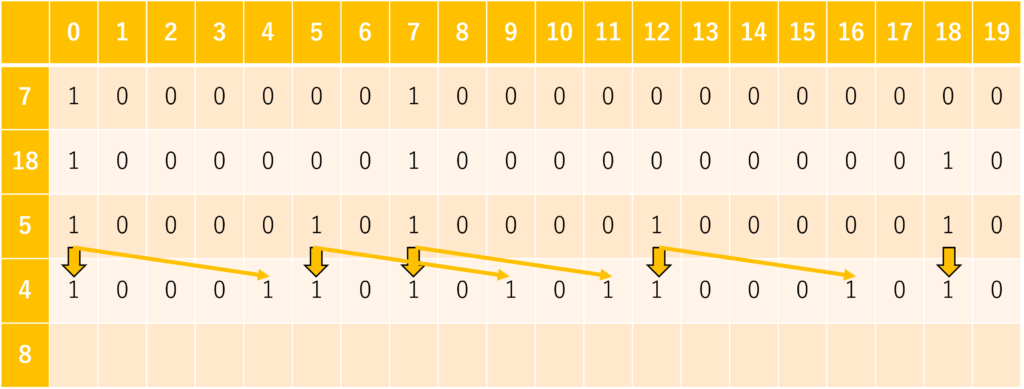
5番目のおもり(\(i = 5\))について
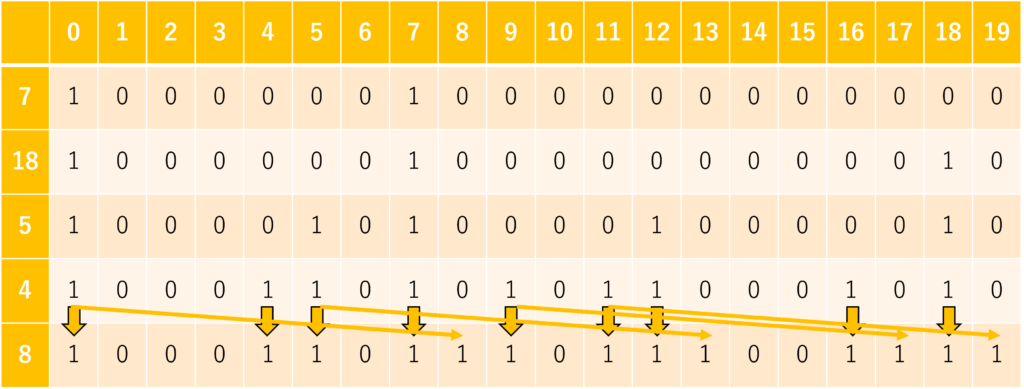
最後に、\(i=n(=5), j=x(=19)\) の値が1,すなわちTrueであるから、
与えられた \(n\) 個のおもりを用いて、重さ\(x\)を「実現できる」ことが分かります。
漸化式を考える
「i 番目のおもりを選ぶことで、重さ\(j\)を実現できるか否か」の判断においては、
(i – 1行目のj列の値) または (i行目の j – A[i]列) の値を参照します。
$$
dp[i][j] = \begin{cases}
dp[i-1][j] \ or \ dp[i-1][j – a[i]] & (A[i] \le j)\\
dp[i-1][j] & (A[i] > j)
\end{cases}
$$
コード例
n, x = map(int, input().split())
A = [int(input()) for i in range(n)]
# n * x の2次元配列を作成
dp = [[0]*(x + 1) for _ in range(n)]
# 1番目のおもり
dp[0][0] = 1
if A[0] <= x:
dp[0][A[0]] = 1
# 2番目以降のおもり
for i in range(1,n):
for j in range(x + 1):
ref = dp[i - 1][j] # ref = reference(参照)の意味
if A[i] > j: # コスト不足のとき
dp[i][j] = ref
else:
ref_back = dp[i - 1][j - A[i]]
dp[i][j] = ref or ref_back
print("yes" if dp[n-1][x] else "no")2. 部分和数え上げ問題:重さの和をxにする方法は何通りあるか?
問題
\(1~n\) の番号がついた \(n\) 個のおもりがあり、おもり \(i\) の重さは \(a_i\) です。おもりを何個か選んで重さの和が \(x\) となるようにする方法が何通りあるか求めてください。なお、同じおもりを2個以上選ぶことはできません。重さが同じおもりが複数存在する場合、それらは区別して別のものとして扱うことにします。答えは非常に大きくなる可能性があるので、答えを 1,000,000,007 で割った余りで出力してください。
引用元:https://paiza.jp/works/mondai/dp_primer/dp_primer_partial_sums_step1
具体例で考える
\(n = 5, x = 10\)
\(a_1 = 7, a_2 = 3, a_3 = 4, a_4 = 3, a_5 = 2\)
の場合を考えます。
1問目と同様、下の表のように記録していきます。縦軸が\(i\) , 横軸が\(j\)です。
しかし、1問目と異なる点があります。
「ある重さ j 」を
「 i 番目のおもりを選ぶことで実現する方法は”何通りか”」という状態を記録していく。
と表現することができます。
これだけでは分かりにくいので、早速、具体的な数値で見ていきます。
1番目のおもり(\(i = 1\))について。おもりを選ぶ(あるいは選ばない)ことで重さ0, 7を実現することができます。それぞれの実現方法は1通りです。ここは簡単です。
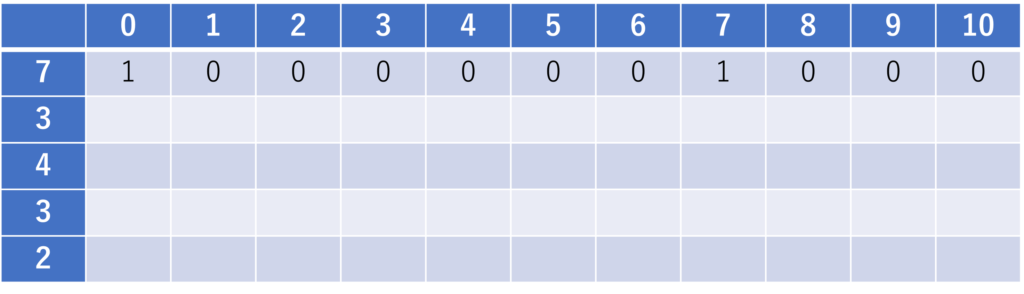
2番目のおもり(\(i = 2\))については、1行目を参照します。
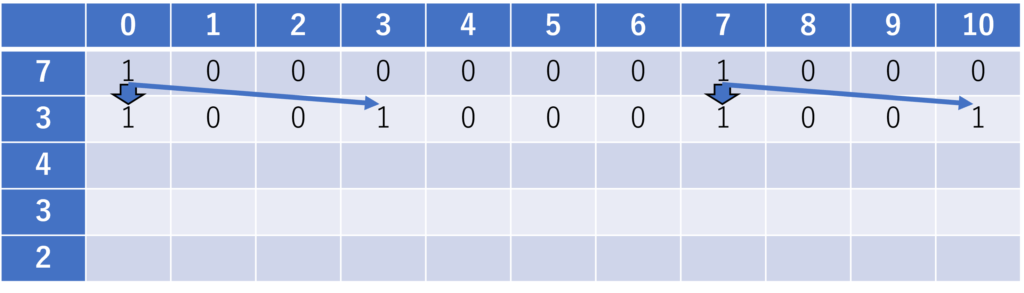
3番目のおもり(\(i = 3\))については、2行目を参照します。
ここで、\(j=7\) の列に着目します。上の行から降ろしている矢印は、「2番目のおもりまでの議論において、\(j=7\)を実現する方法が1通り(重さ7のおもり1つを選ぶ)あった」ことを意味しています。一方、斜めの矢印は、2行目において \(j=3\) を実現する方法が1通り存在するから、重さ4のおもりを選ぶことでも \(j=7\) を実現できることを示しています。
すなわち、現時点で \(j=7\) の実現方法は2通りです。
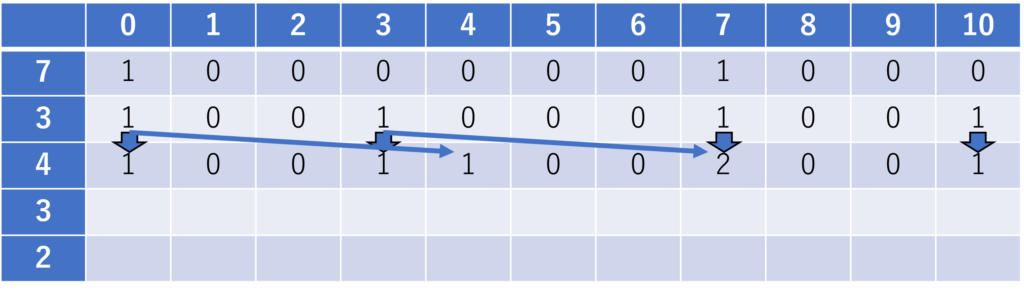
4番目のおもり(\(i = 4\))について
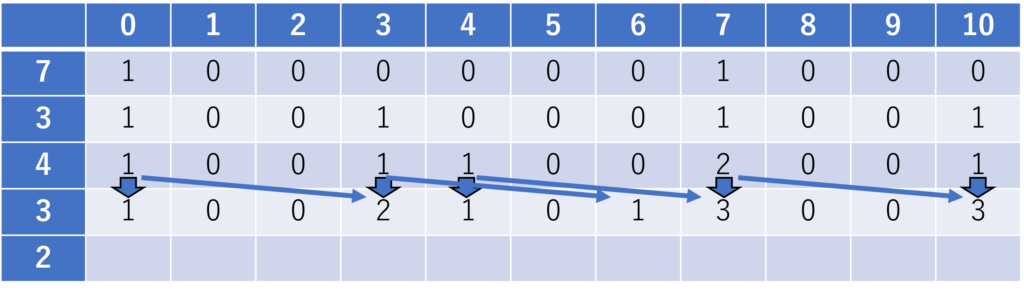
5番目のおもり(\(i = 5\))について

漸化式を考える
(i – 1行目のj列の値) または (i行目の j – A[i]列) の値を参照し、それぞれの値の和を取ればよいです。参照元の値が0であれば、参照していないのと同じだと解釈することができます。
$$
dp[i][j] = \begin{cases}
dp[i-1][j – a[i]] \ + \ dp[i-1][j] & (A[i] \le j)\\
dp[i-1][j] & (A[i] > j)
\end{cases}
$$
コード例
n, x = map(int, input().split())
A = [int(input()) for i in range(n)]
# n * x の2次元配列を作成
dp = [[0]*(x + 1) for _ in range(n)]
# 0列目はすべて1
for i in range(n):
dp[i][0] = 1
dp[0][A[0]] = 1
for i in range(1,n):
for j in range(x + 1):
if A[i] <= j:
dp[i][j] += dp[i - 1][j - A[i]] + dp[i -1][j]
else:
dp[i][j] = dp[i - 1][j]
print(dp[n-1][x]%(10 ** 9 + 7))3. 最小個数部分和問題:重さの和をxにするために必要なおもりは最低何個か?
問題
1 ~ n の番号がついた n 個のおもりがあり、おもり i の重さは a_i です。おもりを何個か選んで重さの和が x となるようにする方法を考えたとき、選ぶおもりの個数の最小値を出力してください。なお、同じおもりを2個以上選ぶことはできません。なお、重さの和が x となるようにおもりを選ぶ方法が存在しない場合は-1と出力してください。
引用元:https://paiza.jp/works/mondai/dp_primer/dp_primer_partial_sums_step2
具体例で考える
\(n = 5, x = 10\)
\(a_1 = 7, a_2 = 3, a_3 = 4, a_4 = 3, a_5 = 2\)
の場合を考えます。
以下の表のように考えていくが、初期値として設定している inf は、無限大の意味です。
理由は、「最小値を更新していく」という過程で、表に入りうるどの数値よりも大きい値が必要だからです。
1番目のおもり(\(i = 1\))について
・おもりを0個選ぶ(選ばない)ことで重さ0を実現できる。
・おもりを1つ選ぶことで重さ7を実現することができる。
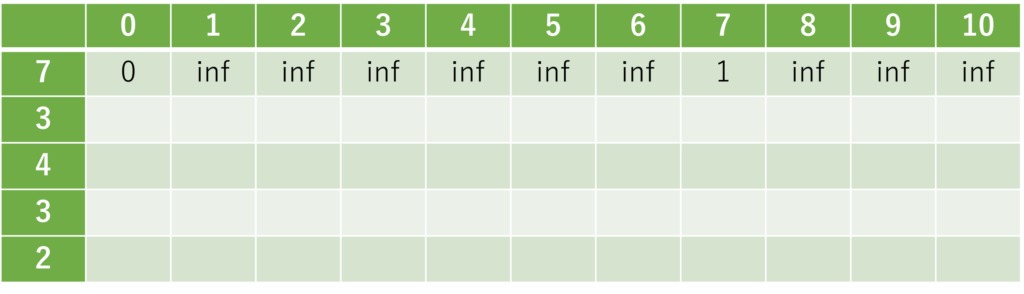
2番目のおもり(\(i = 2\))について。おもりを”選ぶ”場合は、参照元の数値に\(+1\)します。
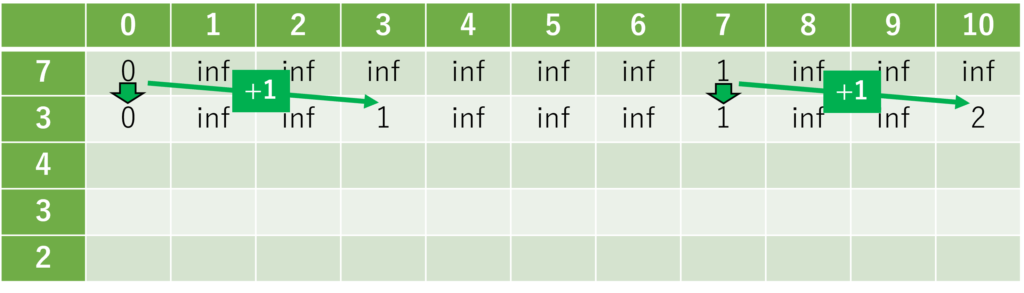
3番目のおもり(\(i = 3\))について。
赤丸で囲んだ場所のように、参照元が2つある際、値が小さくなるほうを採用します。
\((i, j) = (3, 7)\) のマスには、
\((i-1, j-a[i]) = (2, 3) = 2 \ or \ (i-1, j) = (2, 7) = 1\)
のどちらかを選んで入れる必要があります。
よって、2つの数値2, 1を比べて、小さいほうである1を書き入れます。
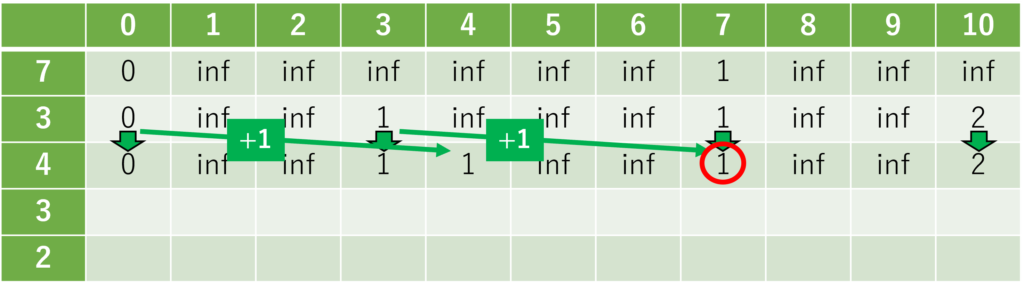
4番目のおもり(\(i = 4\))について。

5番目のおもり(\(i = 5\))について。
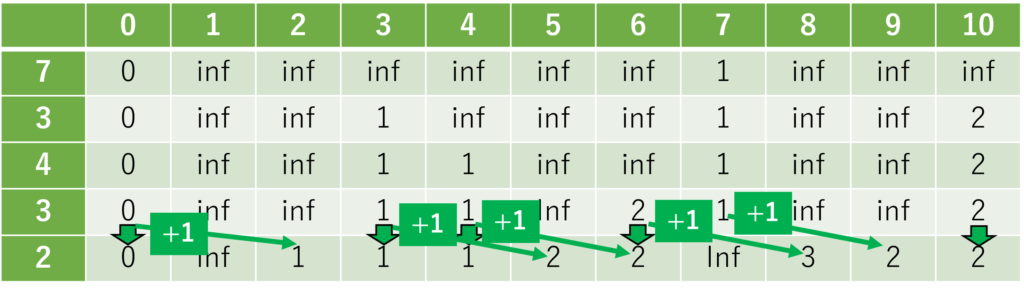
以上より、重さの総和 \(x = 10\) を実現しうる最小のおもりの個数は、2個(重さ7, 3)です。
ちなみに、今回の問題の最終的な答えではありませんが、重さ3, 4, 3の3つのおもりを使っても、重さの総和 \(x = 10\) を実現することができます。
漸化式を考える
$$
dp[i][j] = \begin{cases}
min(dp[i-1][j – a[i]] +1\ , \ dp[i-1][j]) & (A[i] \le j)\\
dp[i-1][j] & (A[i] > j)
\end{cases}
$$
コード例
n, x = map(int, input().split())
A = [int(input()) for i in range(n)]
# n * x の2次元配列を作成
dp = [[10**9]*(x + 1) for _ in range(n)]
# 0列目はすべて0
dp[0][0] = 0
if A[0] <= x:
dp[0][A[0]] = 1
for i in range(1,n):
for j in range(x + 1):
if A[i] <= j:
dp[i][j] = min(dp[i - 1][j - A[i]]+1, dp[i -1][j])
else:
dp[i][j] = dp[i - 1][j]
if dp[n-1][x] == 10**9:
print(-1)
else:
print(dp[n-1][x])4. 個数制限なし部分和問題
問題
1 ~ n の番号がついた n 種類のおもりがあり、おもり i の重さは a_i です。それぞれのおもりは無限個存在しており、任意のおもりを任意の個数使うことができます。
引用元:https://paiza.jp/works/mondai/dp_primer/dp_primer_partial_sums_step3
このとき、おもりを選んで重さの和を x となるようにすることができるかどうか判定してください。
具体例で考える
上記で考えてきた問題と、本質は同じす。
異なる点は、「それぞれのおもりは無限個存在している」を、どのようにして実装するかです。
答えは、
今まで \(i\) 番目のおもりを考えるときは、\(i-1\) 行目の情報を参照していたが、
今回は、\(i\) 番目のおもりを考えるときは、\(i\) 行目の情報も参照すればよい。
ということです。
1番目のおもり(\(i = 1\))について。
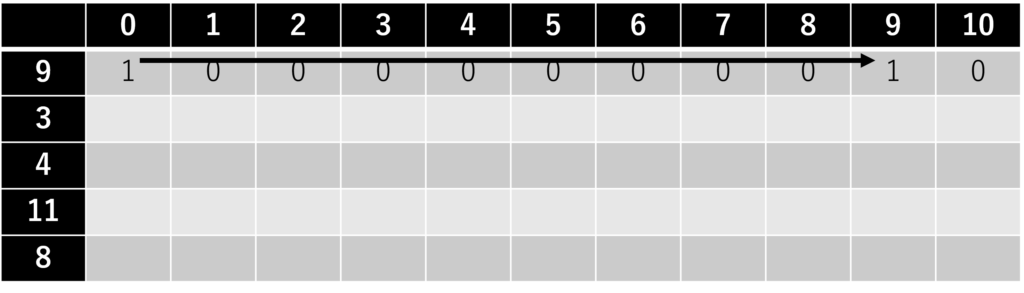
2番目のおもり(\(i = 2\))について。各重さのおもりが無限に存在しているため、
重さ3のおもりを使って、\(j = 3, 6, 9\)を実現できます。
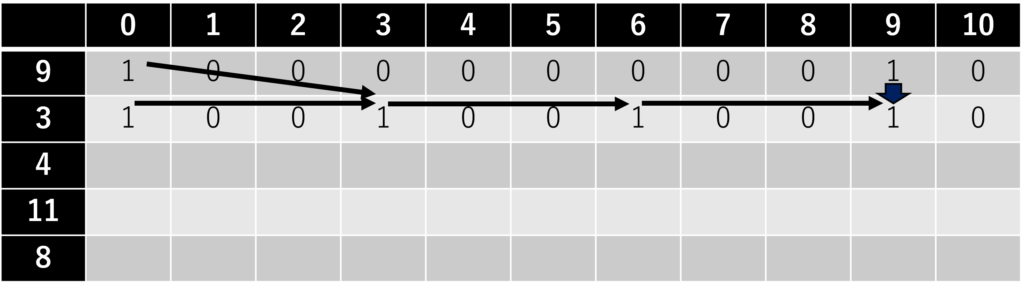
3番目のおもり(\(i = 3\))について。各重さのおもりが無限に存在しているため、
重さ3のおもりを使って、\(j = 4, 7, 10\)を実現できます。
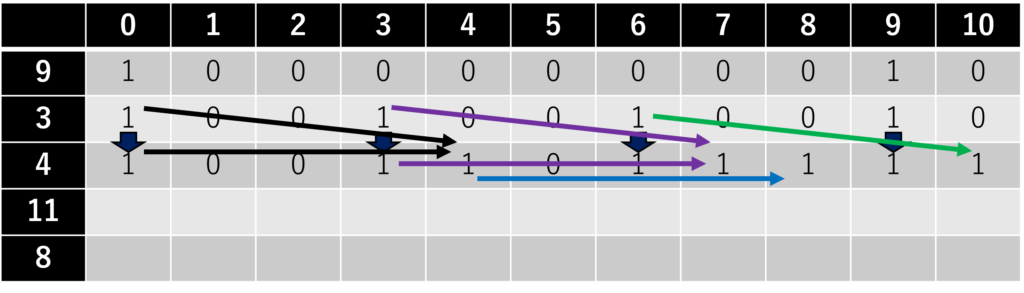
4番目のおもり(\(i = 4\))について。
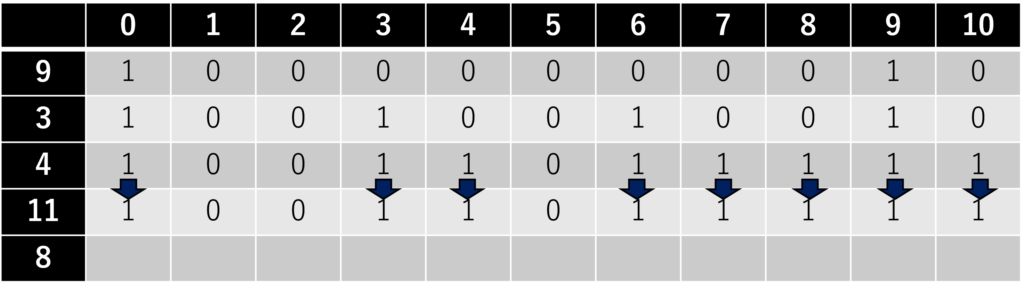
5番目のおもり(\(i = 5\))について。
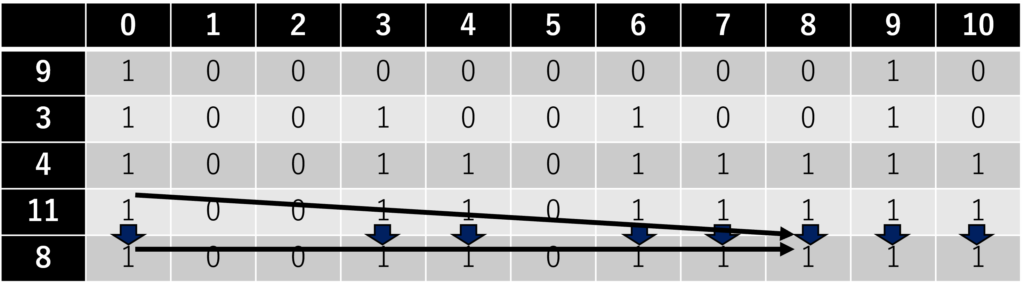
最後に、\(i=n(=5), j=x(=10)\) の値が1,すなわちTrueであるから、
与えられた\(n\)個のおもりを用いて、重さ \(x\) を「実現できる」ことが分かります。
漸化式を考える
$$
dp[i][j] = \begin{cases}
dp[i-1][j – a[i]] \ or \ dp[i-1][j] \ or \ dp[i][j – a[i]] & (A[i] \le j)\\
dp[i-1][j] & (A[i] > j)
\end{cases}
$$
コード例
# 個数制限なし部分和問題
n, x = map(int, input().split())
A = [int(input()) for i in range(n)]
# n * x の2次元配列を作成
dp = [[0]*(x + 1) for _ in range(n+1)]
# 重さ0, 0個目のおもりについて
dp[0][0] = 1
for i in range(1, n+1):
for j in range(x + 1):
ref = dp[i - 1][j] # ref = reference(参照)の意味
if A[i-1] > j: # コスト不足のとき
dp[i][j] = ref
else:
ref_back = dp[i-1][j - A[i-1]]
ref_back_i = dp[i][j - A[i-1]]
# 間違い: dp[i][j] = min(ref,ref_back,ref_back_i) 正しくは下
# dp[i][j] = ref or ref_back or ref_back_i これでも通るが下の方が必要最小限
dp[i][j] = ref or ref_back_i
print("yes" if dp[n][x] else "no")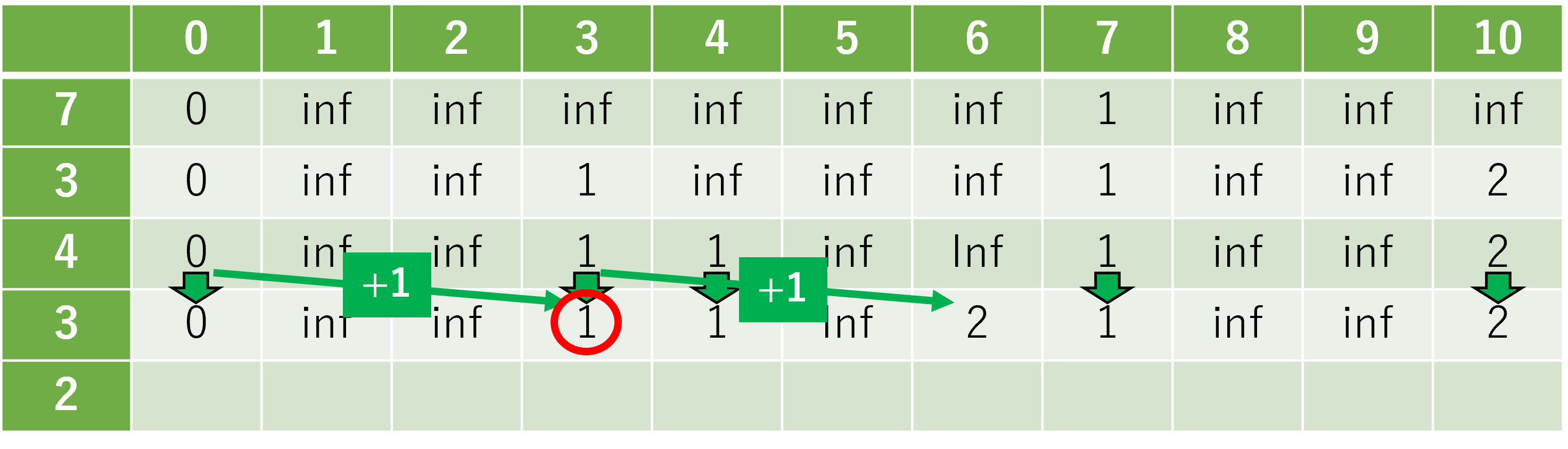


コメント
「最小個数部分和問題」の漸化式、min() の第一引数には +1 が必要では無いでしょうか。
ご指摘ありがとうございます。修正いたしました。
すごく分かりやすくて助かりました!
1つ質問なのですが、個数制限なし部分和問題の18行目は
dp[i][j] = min(ref,ref_back,ref_back_i)
ではなくて
dp[i][j] = ref or ref_back or ref_back_i
みたいな感じではないでしょうか?
コメントありがとうございます。
本記事は、私自身が理解に苦労した点を何とか分かりやすくできないかと思い、書いた記事ですので、そう言っていただけると非常に嬉しいです。
>>dp[i][j] = min(ref,ref_back,ref_back_i)
>>ではなくて
>>dp[i][j] = ref or ref_back or ref_back_i
>>みたいな感じではないでしょうか?
その通りです。こちらのミスでした。申し訳ございません。
コードの部分を修正いたしました。
部分和問題、動的計画法について大変わかりやすく読ませていただきました。
個数制限なし部分和問題について質問です。
遷移の部分、jを小さい方から回す場合に限り、
dp[i][j] = ref or ref_back_i
……でも問題ないように思いますが、どうでしょうか。
(jを小さい方から回しており、dp[i−1][j–a[i]] の情報はすでにdp[i][j–a[i]]へと引き継がれているはずなので)
最終結論がTrueになる場合のパターン数を求めたかったので思案してみたところ、dp[i][j] = ref + ref_back_i としたらいい感じになったようなので。
貴重なコメントをありがとうございます。
> dp[i][j] = ref or ref_back_i
> ……でも問題ないように思いますが、どうでしょうか。
確かに、そちらの記述でも問題ないことを確認しました。
> 最終結論がTrueになる場合のパターン数を求めたかったので思案してみたところ、dp[i][j] = ref + ref_back_i としたらいい感じになったようなので。
他の問題にも応用が利くよう、シンプルな実装を意識していきたいと思います。