問題はこちら。院試対策・物理学の勉強にご利用ください。
また、誤植があればお問い合わせください。
問1:2準位系の統計力学
1-1.
微視的状態数は
$$W = \frac{N!}{n!}{(N-n)!}$$
よって、ボルツマンの原理により
\begin{align*}
S &= k_BlogW\\
&\cong k_B{NlogN-N \ – \ (nlogn – n) \ – \ ((N-n)log(N-n) + (N-n))}\\
&= k_BN{-xlogx \ – \ (1-x)log(1-x)}
\end{align*}
平衡状態では、熱力学第一法則により
$$dU = TdS$$
\(U = \varepsilon n\)であるから
$$\varepsilon dn = TdS$$
$$\frac{\varepsilon}{T} = \frac{\partial S}{\partial n} = \frac{\partial x}{\partial n}\frac{\partial S}{\partial x} = \frac{1}{N}\frac{\partial S}{\partial x}$$
が成り立つ。1-1の結果より
$$\frac{\partial S}{\partial x} = k_BNlog\frac{1-x}{x}$$
すなわち
$$\frac{\varepsilon N}{T} = k_BNlog\frac{1-x}{x}$$
これを変形すると
$$x = \frac{1}{e^{\frac{\varepsilon}{k_BT}}+1}$$
1-3.
$$dW = \frac{N}{e^{\frac{\varepsilon}{k_BT}}+1}d\varepsilon$$
となるが、これを積分する。
$$W = N\int_0^{\varepsilon_1}\frac{1}{e^{\frac{\varepsilon}{k_BT}}+1}d\varepsilon$$
ここで、\(e^{\frac{\varepsilon}{k_BT}} = \alpha\)とおくと、
$$\frac{1}{k_BT}e^{\frac{\varepsilon}{k_BT}}d\varepsilon = d\alpha$$
であるから、先の積分は次のように計算できる。
\begin{align*}
W &= N\int_1^{e^{\frac{\varepsilon_1}{k_BT}}}\frac{1}{\alpha + 1}k_BTe^{-\frac{\varepsilon}{k_BT}}d\alpha\\
&= Nk_BT\int_1^{e^{\frac{\varepsilon_1}{k_BT}}}\frac{1}{\alpha + 1}\frac{1}{\alpha}d\alpha\\
&= Nk_BT\int_1^{e^{\frac{\varepsilon_1}{k_BT}}}\left(\frac{1}{\alpha} – \frac{1}{\alpha + 1}\right)d\alpha\\
&= Nk_BT\left(loge^{\frac{\varepsilon_1}{k_BT}} – lof\frac{e^{\frac{\varepsilon_1}{k_BT}}+1}{2}\right)\\
&= Nk_BTlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT}}}
\end{align*}
1-4.
第一法則より
\begin{align*}
Q &= Nx\varepsilon_1 – Nx\cdot 0 – W\\
&= \frac{N\varepsilon_1}{e^{\frac{\varepsilon_1}{k_BT}}+1} – Nk_BTlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT}}}
\end{align*}
ここで
$$S(x(\varepsilon_1, T)) = k_BN\left(-\frac{1}{e^{\frac{\varepsilon_1}{k_BT}}+1}log{1}{e^{\frac{\varepsilon_1}{k_BT}}+1} – \frac{e^{\frac{\varepsilon_1}{k_BT}}}{e^{\frac{\varepsilon_1}{k_BT}}+1}log\frac{e^{\frac{\varepsilon_1}{k_BT}}}{e^{\frac{\varepsilon_1}{k_BT}}+1}\right)$$
$$S(x(0, T)) = k_BNlog2$$
したがって、\(e^{\frac{\varepsilon_1}{k_BT}}=A\)とおき、
\begin{align*}
& S(x(\varepsilon_1, T)) – S(x(0, T)) \\
&= k_BN\left(-\frac{1}{e^A+1}log\frac{e^{-A}}{e^{-A}+1} – \frac{e^{A}}{e^{A}+1}log\frac{1}{e^{-A}+1}\right) – k_BNlog2\\
&= \frac{1}{T}\left(\frac{N\varepsilon_1}{e^{\frac{\varepsilon_1}{k_BT}}+1} – k_BNTlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT}}}\right)\\
&= \frac{Q}{T}
\end{align*}
よって、
$$Q = T [S(x(\varepsilon_1, T)) – S(x(0, T))]$$
が示せる。また、\(dU = TdS \ (T=const)\)より\(\Delta U , \ \Delta S>0\)であるから\(Q>0\)
問2:循環過程からなる熱機関
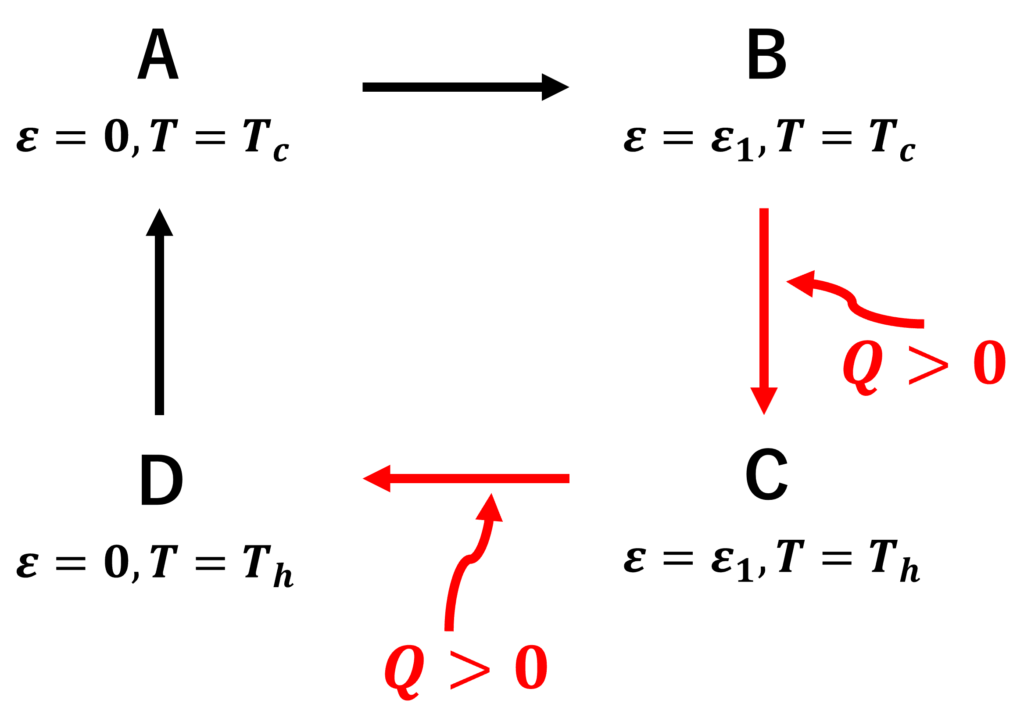
赤矢印で示した過程は、系に高温熱浴から熱が流入していることを表す。
2-1.
第一法則から
\begin{align*}
Q_{B\rightarrow C} &= \Delta U_{B\rightarrow C}\\
&= Nx(\varepsilon_1, T_h)\varepsilon_1 – Nx(\varepsilon_1, T_c)\varepsilon_1\\
&= N\varepsilon_1\left(\frac{1}{e^{\frac{\varepsilon_1}{k_BT_h}}+1} – \frac{1}{e^{\frac{\varepsilon_1}{k_BT_c}}+1}\right)
\end{align*}
2-2.
\(C\rightarrow D\)の過程における仕事は、1-3で求めた\(W\)において\(T=T_h\)とし、負号をつけたものであるから、
\begin{align*}
Q_{C\rightarrow D} &= \Delta U_{C\rightarrow D} – W(T_h, \varepsilon;\varepsilon_1\rightarrow 0)\\
&= Nx(0, T_h)\cdot 0 – Nx(\varepsilon_1, T_h)\varepsilon_1 + Nk_BT_hlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT_h}}}
\end{align*}
$$Q_{C\rightarrow D} = – \frac{N\varepsilon_1}{1+e^{\frac{\varepsilon_1}{k_BT_h}}} + Nk_BT_hlog{2}{1+e^{-\frac{\varepsilon_1}{k_BT_h}}}$$
以上より、
\begin{align*}
Q_h &= Q_{B\rightarrow C} + Q_{C\rightarrow D}\\
&= Nk_BT_hlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT_h}}} \ – \ N\varepsilon_1\frac{1}{e^{\frac{\varepsilon_1}{k_BT_c}}+1}
\end{align*}
2-3.
\begin{align*}
W _{C\rightarrow D} &= -W(W(T_h, \varepsilon;\varepsilon_1\rightarrow 0)\\
&= Nk_BT_hlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT_h}}}
\end{align*}
また、\(A\rightarrow B\)で系が外にする仕事は
\begin{align*}
W _{A\rightarrow B} &= -W(W(T_c, \varepsilon;0\rightarrow \varepsilon_1)\\
&= -Nk_BT_clog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT_c}}}
\end{align*}
以上より、
$$W_{cyc} = Nk_B\left(T_hlog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT_h}}} – T_clog\frac{2}{1+e^{-\frac{\varepsilon_1}{k_BT_c}}}\right)$$
2-4.
\(\varepsilon_1\rightarrow\infty\)とすると、
$$Q_h\rightarrow Nk_BT_hlog2$$
$$W_{cyc} \rightarrow Nk_B(T_h – T_c)log2$$
となることから、
\begin{align*}
\eta &= \frac{W_{cyc} }{Q_h}\\
&= \frac{T_h – T_c}{T_h}\\
&= \eta_c
\end{align*}
が成り立つ。



コメント