間隔を\(d\)だけ離して置かれた2つの点電荷\(+q, -q\)がある.
電荷から十分遠い場所でのポテンシャルを求めよ.
[解]
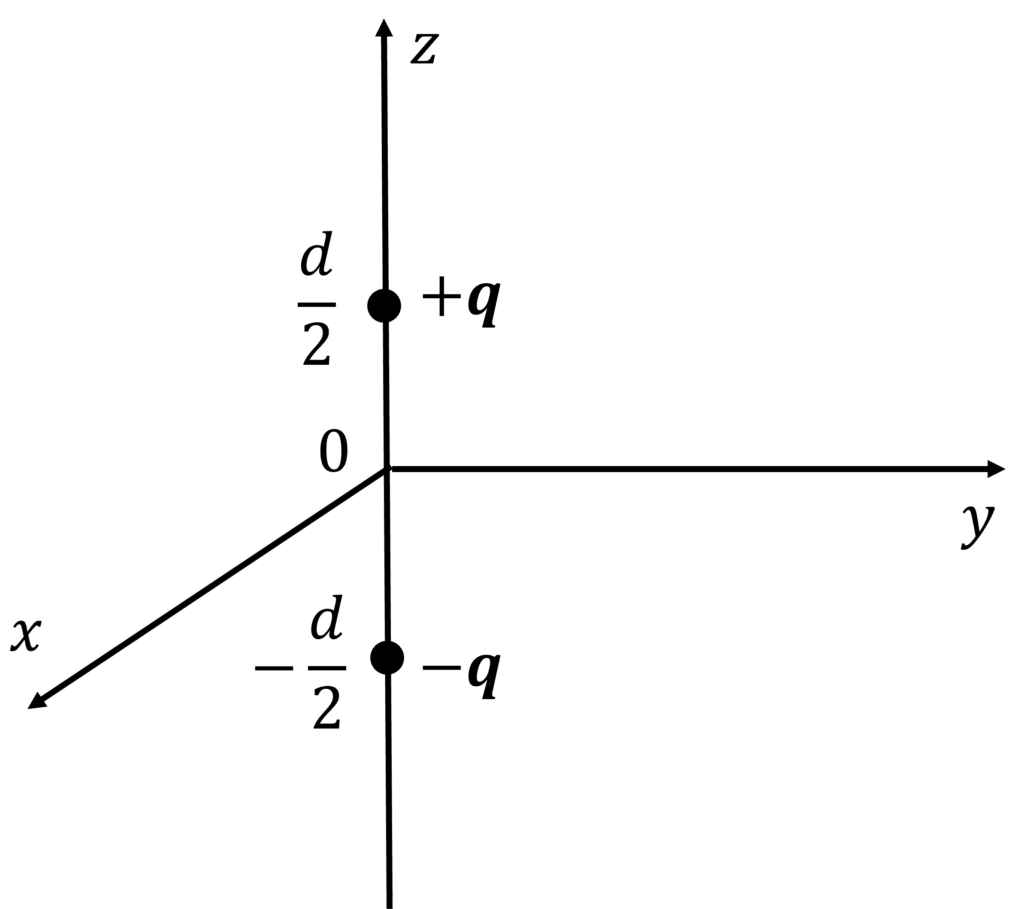
点\(\mathbf{r} = (x, y, z)\)におけるポテンシャル(電位)は,
$$\phi(\mathbf{r}) = \frac{q}{4\pi \varepsilon_0}\left\{\frac{1}{\left[x^2 + y^2 + \left(z-\frac{d}{2}\right)^2\right]^{1/2}} – \frac{1}{\left[x^2 + y^2 + \left(z+\frac{d}{2}\right)^2\right]^{1/2}}\right\}$$
ここで, \((x^2 + y^2 + z^2)^{1/2} = r\)であるから(\(r\)は原点からの距離)
\begin{align*}
& \left[x^2 + y^2 + \left(z\pm\frac{d}{2}\right)^2\right]^{-1/2}\\
& = \left[x^2 + y^2 + z\left(1\pm\frac{d}{z2}\right)^2\right]^{-1/2}\\
& \cong \left[x^2 + y^2 + z\left(1\pm\frac{d}{z}\right)\right]^{-1/2}\\
&= \left(x^2 + y^2 + z^2 \pm zd\right)^{-1/2}\\
&= r^{-1/2}(1 \pm \frac{zd}{r^2})^{-1/2}\\
& \cong r^{-1/2}(1 \mp \frac{zd}{2r^2})
\end{align*}
上の式変形では, 次の近似を用いた.
\(x \ll 1\)の時に成り立つ近似式
$$(1 + x)^\alpha \cong (1 + \alpha x)$$
したがって,
\begin{align*}
\phi (\mathbf{r}) &= \frac{q}{4\pi\varepsilon_0}\left\{\frac{1}{r}\left(1 – \frac{zd}{2r^2}\right) – \left(1 + \frac{zd}{2r^2}\right)\right\}\\
&= \frac{q}{4\pi\varepsilon_0}\frac{zd}{r^3}
\end{align*}
が得られる. よって, 電気双極子による, 無限遠方, すなわち\(d \ll r\)における電位は
$$\phi (\mathbf{r}) = \frac{p}{4\pi\varepsilon_0}\frac{z}{r^3}$$
ただし, 電気双極子モーメント\(p = qd\)を用いた.



コメント