はじめに
mnistなど、手書き文字の識別を題材に画像認識AIのを学習することで、深層学習の基本的な理論・実装方法を体系的に理解することができます。
本記事では、手書き文字の識別において正解率98%以上を達成することのできる深層学習モデルを、TensorflowやPyTorchといったフレームワークを一切使用せずに実装する方法を解説します。
ここで紹介するスクリプトを実行するには、以下のファイル群が必要です。

「バッチ正規化」を導入した畳み込みニューラルネットワークモデルの概要
モデルの簡単な流れは以下の通りです。
- 2次元の画像データがInputとして入ってくる。
※モノクロの場合、画像は2次元データ(縦のサイズ×横のサイズ)となる。しかし、3次元データ(縦のサイズ×横のサイズ×チャンネル数1)とも解釈できる。
RGB画像の場合は、3次元データ(縦のサイズ×横のサイズ×チャンネル数3)である。 - 畳み込み層(Convolution Layer)で画像の特徴が抽出される。畳み込み層におけるパラメータ重みW, バイアスbは学習の対象となる。
- バッチ正規化(Batch Normalization Layer)にて、入力と出力の分布のズレを補正する。
パラメータβ, γが学習の対象となる。 - プーリング層(Pooling Layer)で、画像内におけるオブジェクトのズレを吸収する。
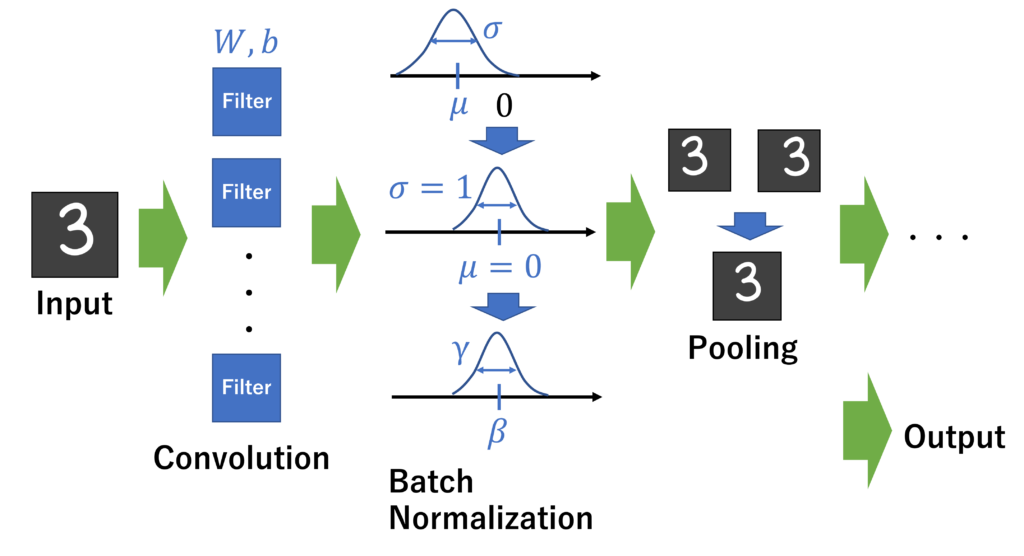
実際には、もう少し複雑な実装となります。
実装の流れ(レイヤの順番)
入力
→
畳み込み層1(W1, b1) → バッチ正規化1(β1, γ1) → 活性化関数(ReLU)→ プーリング層 →
畳み込み層2(W2, b2) → バッチ正規化2(β2, γ2) → 活性化関数(ReLU)→ プーリング層 →
畳み込み層3(W3, b3) → バッチ正規化3(β3, γ3) → 活性化関数(ReLU)→ プーリング層 →
全結合層 (W_Affine1) → バッチ正規化A (β_Affine1, γ_Affine1) → 活性化関数(ReLU)→
全結合層 (W_Affine1) → Softmax関数
→
出力
のようになります。詳しい実装の内容は、GitHubのファイルをご覧ください。
では、実際にモデルを実装して、文字の識別を行ってみましょう。
深層学習モデルを使ってmnist手書き文字を識別する
ここでは、メインとなるminst_cnn.ipynbファイルでのコードを解説していきます。
各種レイヤ・関数群の実装についてはGitHub内のcommonフォルダ内の.pyファイルをご覧ください。
minst手書き数字画像の読み込み
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
from dataset.mnist import load_mnist
(train_data, train_label), (test_data, test_label) = load_mnist(flatten=True, normalize=True, one_hot_label=True)
print(train_data.shape)
print(train_label.shape)
print(test_data.shape)
print(test_label.shape)load_mnistの3つの引数には、以下のような意味があります。1つ目と3つ目は今回作成したコード群が正常に動作するために必須です。また、2つ目は学習を安定させるために重要です。
- flatten=Trueで28*28の2次元データを長さ784の1次元データに平坦化することができる。
- normalize=Trueでデータを正規化(0-255の値を0-1の範囲に収める)できる。
- one_hot_label=Trueで0-9の正解ラベルをベクトルで表現することができる。
必要なライブラリのインポート
まず、データ拡張に用いるImageDataGeneratorをインポートするためには、tensorflowがインストールされている必要があります。手順は以下のようになります。ImageDataGeneratorによるデータ拡張では、画像の拡大縮小・回転を行い、データ量の水増しをすることができます。データ数が少ないとき、このテクニックが役に立ちますが、今回は60,000もの訓練データが存在するので、必要無いかもしれません。しかし、汎用性が高く、知っておいて損はないため、以下のコード内にもコメントアウトで使用方法を記載しておきます。
pip install tensorflowimport tensorflow
print(tensorflow.__version__)
# >> 2.9.1from tensorflow import keras
print(keras.__version__)
# >> 2.9.0今回用いるメインのライブラリをインポートします。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import pickle
from common.optimizer import Adam
from common.ConvNet import ConvNet
from keras.preprocessing.image import ImageDataGenerator学習
train_data = train_data.astype('float32')
#train_data = train_data.reshape(-1, 28*28) : flatten=Trueの代わりになる
#データの正規化
#train_data = (train_data - train_data.min()) / train_data.max() : normalize=Trueの代わりになる
print("train_data.shape=", train_data.shape)
# >> train_data.shape= (60000, 784)epochs = 15
batch_size = 64
optimizer = Adam()
# CNNのオブジェクト生成
snet = ConvNet()
train_loss = []
test_loss = []
train_accuracy = []
test_accuracy = []
##データ拡張器
##datagen = ImageDataGenerator(rotation_range = 10, height_shift_range = 0.1,width_shift_range = 0.1,zoom_range= 0.1)
def __train(epochs):
# 学習に時間がかかりすぎるので、ここでは4000データだけ使用した
train, test, train_labels, test_labels = train_test_split(train_data[:4000], train_label[:4000], test_size=0.3,shuffle=True)
train = train.reshape(-1, 1, 28, 28)
test = test.reshape(-1, 1, 28, 28)
x = train
t = train_labels
x = x.reshape(-1,1,28,28) # 配列形式の変形
# 繰り返し回数
xsize = x.shape[0]
iter_num = np.ceil(xsize / batch_size).astype(np.int)
x = x.reshape(-1,1,28,28) # 配列形式の変形
for epoch in range(epochs):
print("epoch=%s"%epoch)
# シャッフル
idx = np.arange(xsize)
np.random.shuffle(idx)
for it in range(iter_num):
"""
ランダムなミニバッチを順番に取り出す
"""
print("it=", it)
mask = idx[batch_size*it : batch_size*(it+1)]
# ミニバッチの生成
x_train = x[mask]
t_train = t[mask]
##g = datagen.flow(x_train, batch_size = batch_size,shuffle=False)
##batches = g.next()
batches = x_train
# 勾配の計算 (誤差逆伝播法を用いる)
grads = snet.gradient(batches, t_train)
# 更新
optimizer.update(snet.params, grads)
## 学習経過の記録
# 訓練データにおけるloss
# print("calculating train_loss")
train_loss.append(snet.loss(x, t))
# print("calculating test_loss")
# テストデータにおけるloss
test_loss.append(snet.loss(test, test_labels))
# print("calculating train_accuracy")
# 訓練データにて精度を確認
train_accuracy.append(snet.accuracy(x, t))
# print("calculating test_accuracy")
# テストデータにて精度を算出
test_accuracy.append(snet.accuracy(test, test_labels))
return train_accuracy, train_loss, test_accuracy, test_loss 学習は、__train()によって開始されます。左辺に記述した4つの変数に、各エポックにおける評価値が格納されます。
train_accuracy, train_loss, test_accuracy, test_loss = __train(epochs)# 評価性能を可視化する
df_log = pd.DataFrame({"train_loss":train_loss,
"test_loss":test_loss,
"train_accuracy":train_accuracy,
"test_accuracy":test_accuracy})
df_log.plot()
plt.ylabel("loss or accuracy")
plt.xlabel("epochs")
plt.show()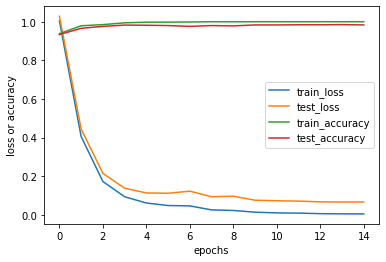
学習を重ねるにつれて、性能が向上していることが分かります。10エポック目辺りから正解率・損失ともに横ばい状態になっているため、エポック数は10程度でも十分であることが分かります。
テストデータに対する汎化性能評価
では、いよいよテストデータ(未知のデータ)に対する性能を評価してみましょう。
test_data = test_data.reshape(-1, 1, 28, 28)
snet.accuracy(test_data, test_label)
# >> 0.9828正解率は98%を超えました!ちなみに、バッチ正規化を導入せず、畳み込み層のみで実装した場合の正解率はおおよそ90%となります。バッチ正規化が以下に有効なのか分かりました。
ImageDataGeneratorによるデータ拡張について
# 上記コードより抜粋
datagen = ImageDataGenerator(rotation_range = 10, height_shift_range = 0.1,width_shift_range = 0.1,zoom_range= 0.1)
...
for epoch in range(epochs):
g = datagen.flow(x_train, batch_size = batch_size,shuffle=False)
batches = g.next()
各エポックでnext()関数を呼び出すごとに、batch_size個の画像データが生成されます。上記で紹介したコード内ではデータ拡張は行いませんでしたが、コメントアウトを外すことで実装できます。
重みだけをpickleで保存することでデータ量を削減する
バッチ正規化における最適化対象のパラメータは、β, γです。しかし、実際には移動平均のパラメータmoving_mean, moving_varが最適化されます。両者は同義ですが、実装の際には注意したいです。
# 重みW, バイアスbの保存
with open("mnist_weight.pickle", "wb") as f:
pickle.dump(snet.params, f)
# バッチ正規化の学習結果である移動平均を保存
with open("mnist_mv.pickle", "wb") as f:
pickle.dump(snet.mv, f)保存した重み・移動平均を呼び出して、モデルを再現します。
import pickle
from common.ConvNet_test import ConvNet_test
def func_predict(test_data, test_label):
model = ConvNet_test()
accuracy = model.accuracy(test_data, test_label)
loss = model.loss(test_data, test_label)
return loss, accuracy
func_predict(test_data, test_label)
# >> 0.982モデルごと保存せずとも、パラメータだけを保存・呼び出すことでも、問題なく学習済みモデルを再現することができました。
最後に
今回工夫、および苦労した点は以下の3点です。
- バッチ正規化の導入
- ImageDataGeneratorを用いたデータ拡張
- pickleを用いたパラメータの保存(特に移動平均パラメータの保存)
これらは汎用的な手法でもあるので、今回の経験は今後の勉強にも生かせそうです。
なお、本記事は、深層学習の最も有名な書籍のひとつである、「ゼロから作るDeepLearning」及び、SkillUpAI社の長期インターンシップでの学習コンテンツを参考にしております。

コメント