最長増加部分列 (Longest Increasing Subsequence, LIS)
文字通り、配列があったとき、単調増加になっている、最も長い部分のこと。
例えば、
1, 2, 3, 4, 5
の最長増加部分列は、1, 2, 3, 4, 5そのものであるし、
10, 2, 3, 5, 7, 1, 4, 6
の最長増加部分列は2, 3, 5, 7である。
最長増加連続部分列
n 人が横一列に並んでいます。左から i 番目の人を人 i と呼ぶことにします。人 i の身長は a_i [cm]です。人 l ,人 l+1, … , 人 r からなる区間 [l, r] について、すべての l ≦ i < r に対して a_i ≦ a_{i+1} が成り立っているとき、区間 [l, r] は背の順であると呼ぶことにします。また、区間 [l, r] の長さを r-l+1 とします。
引用元:https://paiza.jp/works/mondai/dp_primer/dp_primer_lis_continuous_step0
背の順であるような区間のうち、最長であるものの長さを出力してください。
考え方
- 要素を前から一つずつ見ていく。
- 現在見ている要素が、一つ手前の要素以上であれば、増加列の長さを+1する。
- 現在見ている要素が、一つ手前の要素より小さければ、増加列の長さを1にリセットする。
この繰り返しを行っていけばよい。
コード例
n = int(input())
dp = [0]*(n+1)
dp[1] = 1
a = int(input())
for i in range(2,n +1):
tmp = int(input())
if a <= tmp :
dp[i] = dp[i-1]+1
else:
dp[i] = 1
a = tmp
print(max(dp))最長部分増加列(非連続)
\(n\) 本の木が横一列に並んでいます。左から \( i\) 番目の木を木 i と呼ぶことにします。木 \(i\) の高さは \(a_i\) [cm] です。
引用元:https://paiza.jp/works/mondai/dp_primer/dp_primer_lis_step0
あなたは、何本かの木を伐採することによって、残った木を左から順に見ると高さが単調増加になっているようにしたいと考えています。つまり、残った木を左から 木 \(k_1\), 木 \(k_2\), … , 木 \(k_m\) とすると、\(a_{k_1} < a_{k_2} < … < a_{k_m}\) が満たされているようにしたいです。なるべく多くの木が残るように、伐採する木を工夫して選んだとき、伐採されずに残る木の本数が最大でいくつになるか求めてください。
なお、最初から \(n\) 本の木が単調増加に並んでいる場合は、1本も伐採しなくてよいものとします。
考え方
増加部分列とは、ある数列の内、左から見たときに単調増加になっている部分のことである。
よって、この問題では、何本かの木を切ってできる「最長」の「増加部分列」を求めたい。
まず、1つの例を考えてみよう。
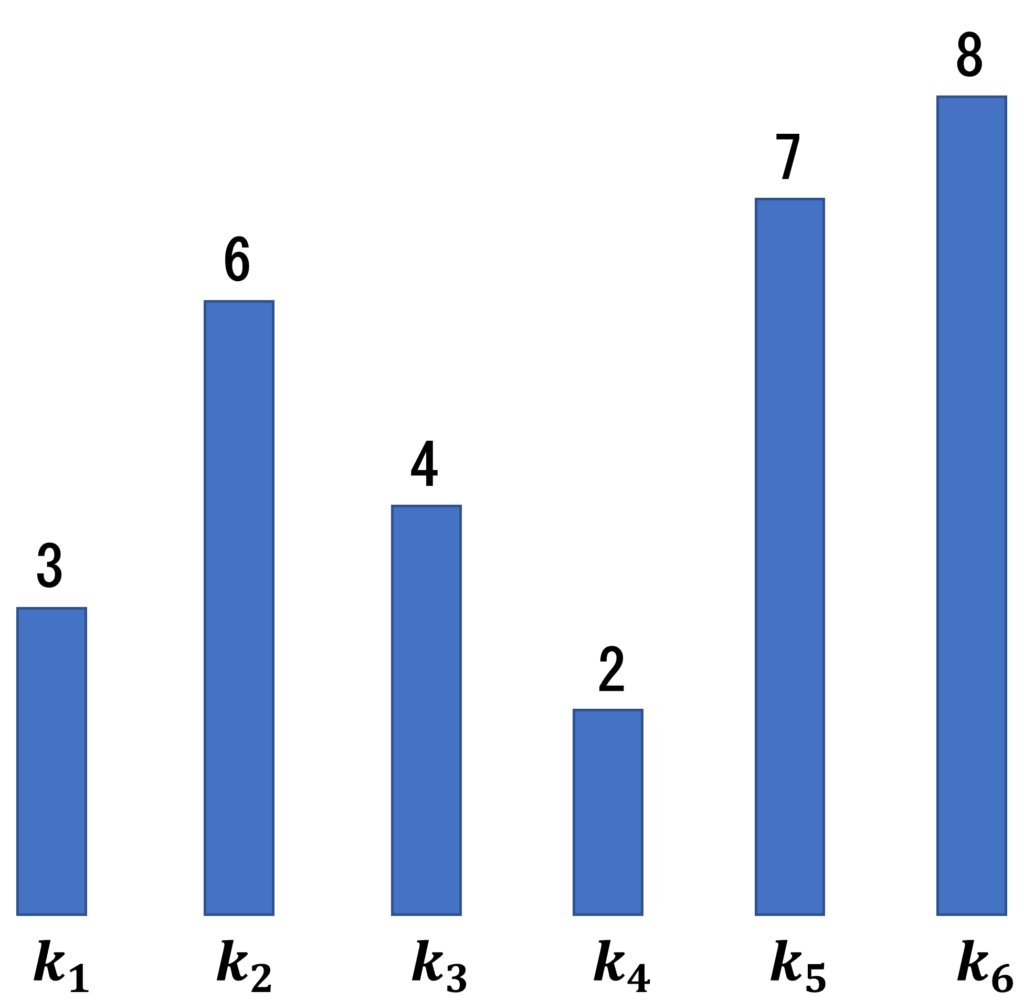
最も長いのは[3, 6, 7, 8]を選んだ時だと分かる。
問題のヒントの部分を参考に、「動的計画法」的な考え方をしてみる。まず、\(dp[k]\)を最後が木kであるような増加部分列のうち、最長の長さのものとする。また、\(dp[i] \ (1 \le i \le k-1)\) はすべて求まっているとする。
木 \(i \ (1 \le i \le k-1)\)からできる最長増加部分列、すなわち、
残った木\(j \ (1 \le j \le m)\)のうち、右端の木 \(m\) の高さ < 木 \(k\) の高さとなる時、
\(dp[k] = dp[m] + 1\)となり、最長増加部分列の長さが更新される。一方、
右端の木 \(m\) の高さ < 木 \(k\) の高さとなる時、\(dp[k] = dp[m]\)となる。
コード例
n = int(input())
a = [int(input()) for _ in range(n)]
dp = [0]*(n+1)
dp[1] = 1
for i in range(2, n+1):
dp[i] = 1
for j in range(1, i):
if a[j-1] < a[i-1]:
dp[i] = max(dp[i], dp[j]+1)
print(max(dp))計算量をO(N^2)からO(NlogN)に削減したい
上での解法は、\(i\) 番目の要素に注目するとき、\(j \ (1 \le j \le i-1)\) 番目のすべての要素と比較する必要があるため、計算量は
\begin{align*}
num_of_loop &= 1 + 2 + … n-1\\
&\cong \sum_{i=1}^n n\\
&= \frac{1}{2}n(n+1)
\end{align*}
となり、\(O(n^2)\)となってしまう。DPと言えば、計算量を削減できるイメージがあったのだが、これでアルゴリズムの恩恵を受けている気がしない。そこで、計算量を\(O(nlogn)\)程度に抑える方法が無いか調べたところ、次の記事を発見した。

↑では簡潔な解説が書かれていたので、ここでは段階的に理解していこう。
考え方
まず、二分探索を使えないかと考える。二分探索の定石として、今回の問題であれば「長さ k の増加部分列は実現可能か」の境界を求めたくなる。ちなみに、長さ3の増加部分列が存在するならば、必ず長さ2の増加部分列も存在するので、上記のような境界は必ず存在する。
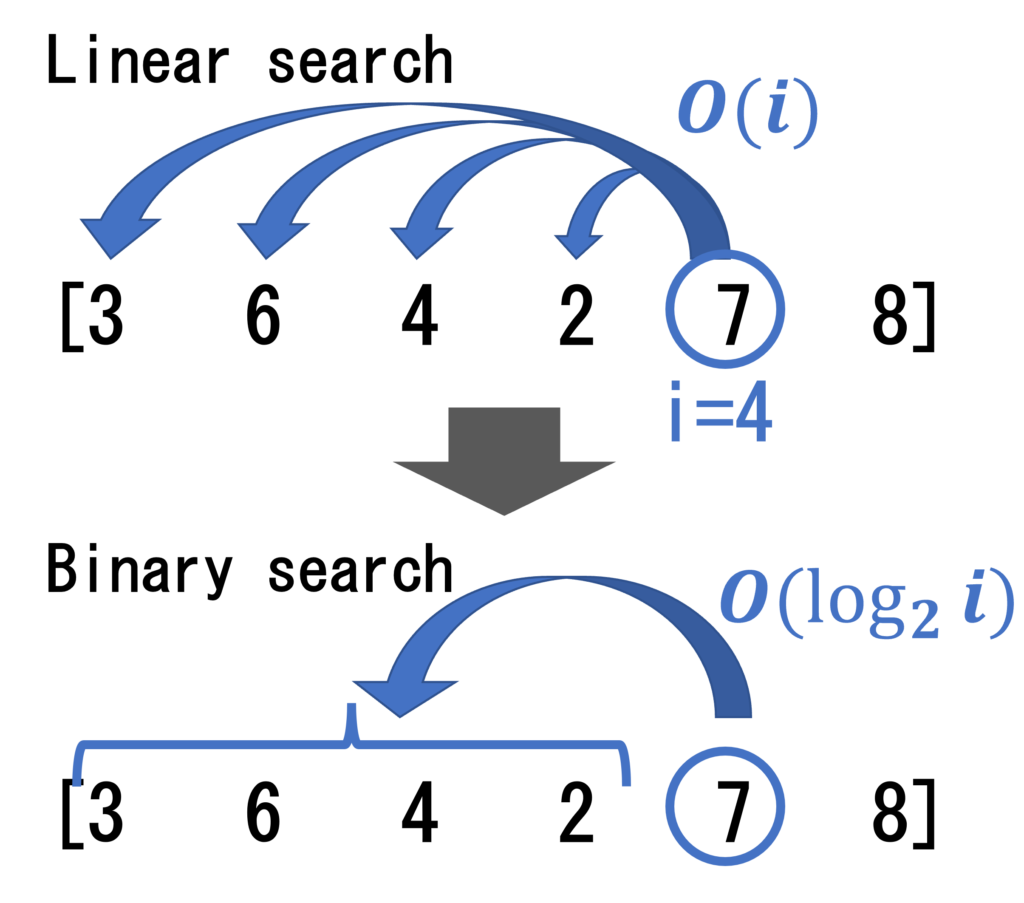
ここで、動的計画法も用いるためには、dp[k]がdp[k-1]の情報を上手く引き継ぐ必要がある。
DPでは、過去の必要な情報だけを残し、その中から効率的に探索を行うことがカギとなる。
増加部分列に新たな要素をつけ足せるかを知るためには、既存の部分増加列の右端の要素と、新たな要素の大きさを比較する必要がある。後者の方が大きければ、部分増加列が1だけ長くなる。よって、
dp[j] = ” 長さ j の増加部分列の中で、各列の右端となる要素の最小値 “
として格納すればよい。実装する前に、上記のようなdpの挙動を確認してみよう。
Loop1 : idx = bisect([], 3) = 0
dp[0] = 3 => dp = [3]
Loop2 : idx = bisect([3], 6) = 1
dp[1] = 6 => dp = [3, 6]
Loop3 : idx = bisect([3, 6], 4) = 1
dp[1] = 4 => dp = [3, 4]
Loop4 : idx = bisect([3, 4], 2) = 0
dp[0] = 2 => dp = [2, 4]
Loop5 : idx = bisect([3, 4], 7) = 2
dp[2] = 7 => dp = [2, 4, 7]
Loop6 : idx = bisect([3, 4, 7], 8) = 3
dp[3] = 8 => dp = [2, 4, 7, 8]
結果として、dpの長さは4であり、これが求めたい結果となる。dpそのものが、最長部分増加列とはなっていないことに注意したい。実際の最長部分増加列は、[3, 4, 7, 8]である。
コード例
from bisect import bisect
N = int(input())
A = [int(input()) for _ in range(N)]
def LIS(N, A):
INF = 10**10
dp = [INF]*(N+1)
dp[0] = -1
for a in A:
# a_iの挿入位置を二分探索で探す
idx = bisect(dp, a)
# 部分増加列の長さ+1(INF <= a_i)or dpの有限の要素と入れ替わる
dp[idx] = min(a, dp[idx])
return max(i for i in range(N+1) if dp[i] < INF)
print(LIS(N,A))実装の際には、以下のような注意点がある。
- \(dp[0]\) の扱いに気を付ける(絶対に \(a_i\)が \(dp[0]\) より小さくならないようにしたい)。よって、\(dp[0] = -1\) としている。
- 長さN+1の配列をあらかじめ用意しつつ、二分探索において \(a_i\)が 適切な挿入位置を探せるように、(\(dp[0]\) を除く)全要素を非常に大きな値に設定しておく必要がある。
まとめ
動的計画法のみで解く際には、直感的な考え方ができるメリットがある一方で、計算量はO(N^2)となってしまうデメリットがあった。一方、「部分増加列を長くしていく」過程において、単調性に注目すると、二分探索が使えることには感銘を受けた。「問題が解けたら良し」ではなく、計算量をもっと少なくできないかを追求していきたい。
コメント