静電場の基本的な事項である,
- 点電荷の作る電場のベクトル形式.
- 電場の重ね合わせの原理.
これらを扱い, 2つの点電荷の作る電場を, ベクトルとして求めます.
よく使う近似式や, やや長々とした計算に慣れましょう.
問題
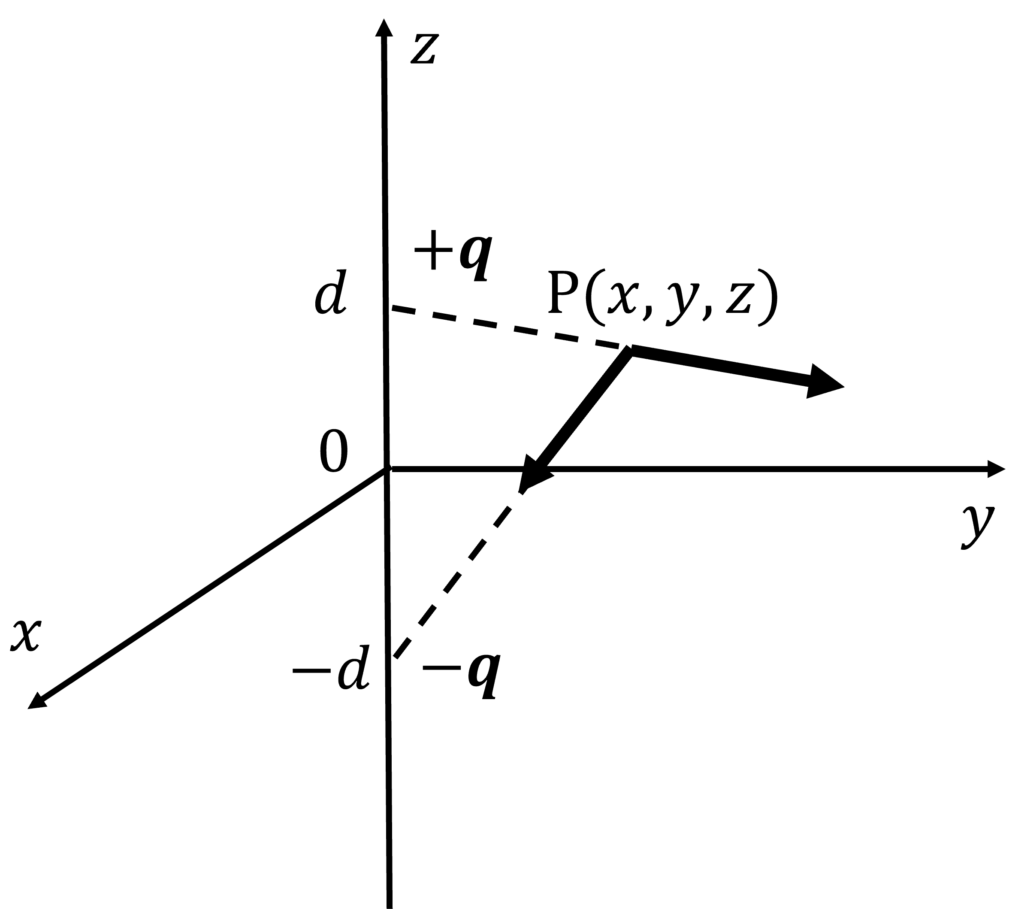
点A \((0, 0, d)\) 及び, B \((0, 0, -d)\)にそれぞれ\(+q\), \(-q\)の点電荷が置かれているとき, 点P\((x, y, z)\)に生じる電場\(\mathbf{E}\)を求めよ. 特に, 点Pが原点Oから十分離れている場合, 点Pにおける電場はどのように表されるか.
解)
点Pにおいて,
i) 電荷\(+q\)による電場
$$\mathbf{E}_A = \frac{q}{4\pi\varepsilon_0}\frac{1}{(x^2 + y^2 + (z – d)^2)^\frac{3}{2}}\cdot (x, y, z – d)$$
ii) 電荷\(+q\)による電場
$$\mathbf{E}_B = \frac{q}{4\pi\varepsilon_0}\frac{1}{(x^2 + y^2 + (z + d)^2)^\frac{3}{2}}\cdot (x, y, z + d)$$
したがって, 重ね合わせの原理により,
\begin{align*}
\mathbf{E} &= \mathbf{E}_A + \mathbf{E}_B \\
&= \left\{\frac{q}{4\pi\varepsilon_0}\frac{x}{(x^2 + y^2 + (z – d)^2)^\frac{3}{2}} \ – \ \frac{q}{4\pi\varepsilon_0}\frac{x}{(x^2 + y^2 + (z + d)^2)^\frac{3}{2}} \right\}\mathbf{i} \\
& \ + \ \left\{\frac{q}{4\pi\varepsilon_0}\frac{y}{(x^2 + y^2 + (z – d)^2)^\frac{3}{2}} \ – \ \frac{q}{4\pi\varepsilon_0}\frac{y}{(x^2 + y^2 + (z + d)^2)^\frac{3}{2}} \right\}\mathbf{j} \\
& \ + \ \left\{\frac{q}{4\pi\varepsilon_0}\frac{z}{(x^2 + y^2 + (z – d)^2)^\frac{3}{2}} \ – \ \frac{q}{4\pi\varepsilon_0}\frac{z}{(x^2 + y^2 + (z + d)^2)^\frac{3}{2}} \right\}\mathbf{k}
\end{align*}
また, 点Pが原点Oから十分に離れているとき, \(z \gg d\)であることを用いると,
$$(z – d)^2 = z^2 \left(1 – \frac{z}{d}\right)^2 \cong z^2\left(1 – 2\cdot\frac{d}{z}\right)$$
$$(z – d)^2 = z^2 \left(1 + \frac{z}{d}\right)^2 \cong z^2\left(1 + 2\cdot\frac{d}{z}\right)$$
と近似できる. ここで,
\(x \ll 1\)の時に成り立つ近似式
$$(1 + x)^\alpha \cong (1 + \alpha x)$$
を用いた. さらに, \(\sqrt{x^2 + y^2 + z^2} = r\)とおくと, 上と同様の近似により,
\begin{align*}
[x^ + y^2 + (z – d)^2]^{-3/2} &\cong (x^2 + y^2 + z^2 – 2dz)^{-3/2}\\
&= \left(^2\left(1 – \frac{2dz}{r^2}\right)\right)^{-3/2}\\
&= r^{-3}\left(1 – \frac{2dz}{r^2}\right)^{-3/2}\\
&\cong r^{-3}\left(1 – \left( – \frac{3}{2}\right)\frac{2dz}{r^2}\right)\\
&= r^{-3}\left(1 + \frac{3dz}{r^2}\right)
\end{align*}
これとほぼ同じ計算を行うと
$$[x^ + y^2 + (z – d)^2]^{-3/2} \cong r^{-3}\left(1 – \frac{3dz}{r^2}\right)$$
も得られる. ちなみに, \(\mathbf{i}, \mathbf{j}, \mathbf{k}\)はそれぞれ, x, y, z方向の単位ベクトルである. 以上の結果を合わせて電場ベクトルの表式を整理すると,
\begin{align*}
\mathbf{E} &= \frac{qx}{4\pi\varepsilon_0}\left\{r^{-3}\left(1 + \frac{3dz}{r^2}\right) – r^{-3}\left(1 – \frac{3dz}{r^2}\right)\right\}\mathbf{i}\\
& \ + \ \frac{qy}{4\pi\varepsilon_0}\left\{r^{-3}\left(1 + \frac{3dz}{r^2}\right) – r^{-3}\left(1 – \frac{3dz}{r^2}\right)\right\}\mathbf{j}\\
& \ + \ \frac{q}{4\pi\varepsilon_0}\left\{(z – d)r^{-3}\left(1 + \frac{3dz}{r^2}\right) – (z + d)r^{-3}\left(1 – \frac{3dz}{r^2}\right)\right\}\mathbf{k}\\
&= \frac{2qd}{4\pi\varepsilon_0}\frac{3xz}{r^5}\mathbf{i} + \frac{2qd}{4\pi\varepsilon_0}\frac{3yz}{r^5}\mathbf{j} + \frac{2qd}{4\pi\varepsilon_0}\frac{3z^2 – r^2}{r^5}\mathbf{k}
\end{align*}
が得られる.
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市著



コメント