以下、更新式とコード例は「ゼロから作るDeepLearning」から引用した。
SGD(確率的勾配降下法)
ランダムに取り出したデータを用いて、パラメータ(重み)\(\mathbf{W}\)を更新していく勾配降下法である。すなわち、SGDは”ミニバッチ学習”の1つでもある。
更新式
\begin{align*}
& \mathbf{W}_{t+1} = \mathbf{W}_t \ – \ \eta\frac{\partial L}{\partial \mathbf{W}_t}\\
& \mathbf{W}_t \ : \ パラメータ(重み)\\
& L \ : \ 損失関数\\
& \eta \ : \ 学習係数(正の値)
\end{align*}
\(\frac{\partial L}{\partial \mathbf{W}_t}\)は、損失関数\(L\)の勾配を表している。
勾配は何度も登場するので、定義を確認しておく。
勾配(ベクトル)とは、「今居る地点から、微小に動いたときに、関数の値が一番大きくなる向き」と、「その微小な動きに対する関数の値の増加量」を表す(ベクトル)量である。
上記の更新式は、
「学習が進むにつれて、重み\(\mathbf{W}\)ベクトルは、勾配ベクトルと逆向きの地点に向かって更新されていく」
ことを意味している。つまり、(基本的に)坂を下ることはあっても上ることはない。とはいえ、更新量が大きすぎる場合は、移動量が過大となり、「更新後の重みが、より大きな損失関数の値を与えてしまう」ということはありうる。
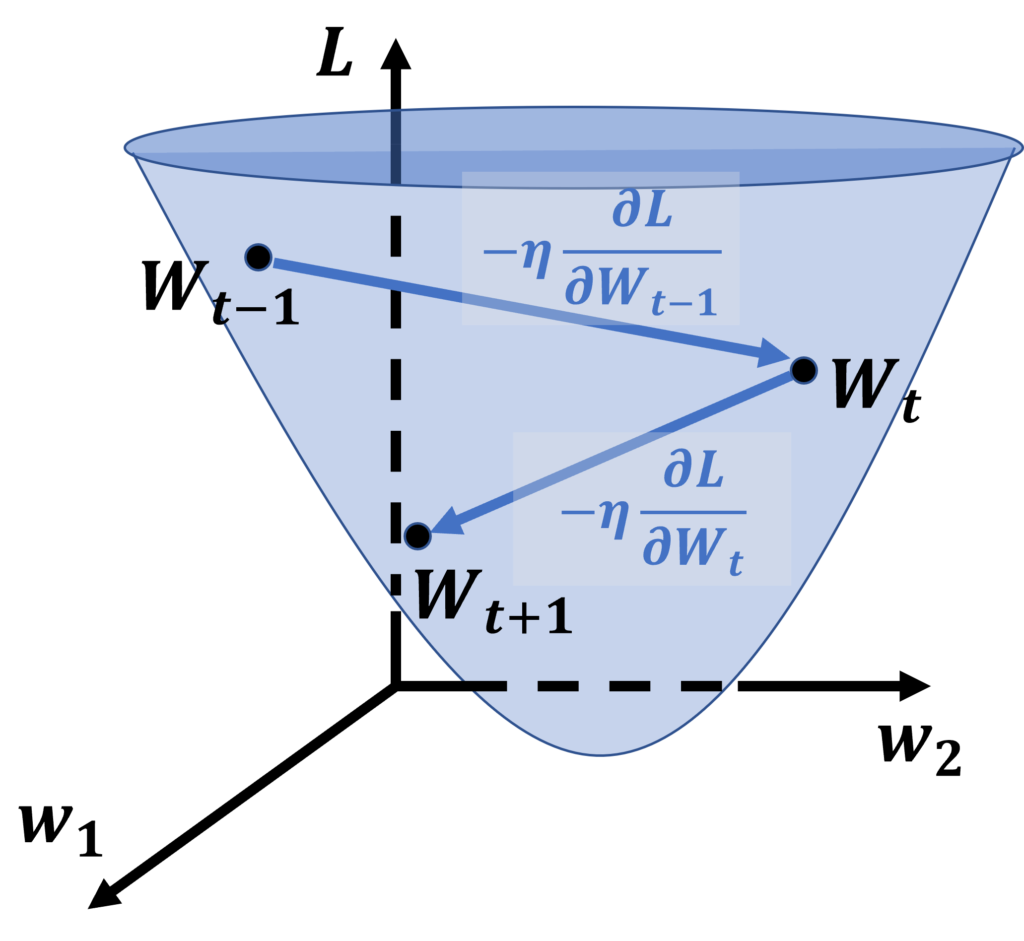
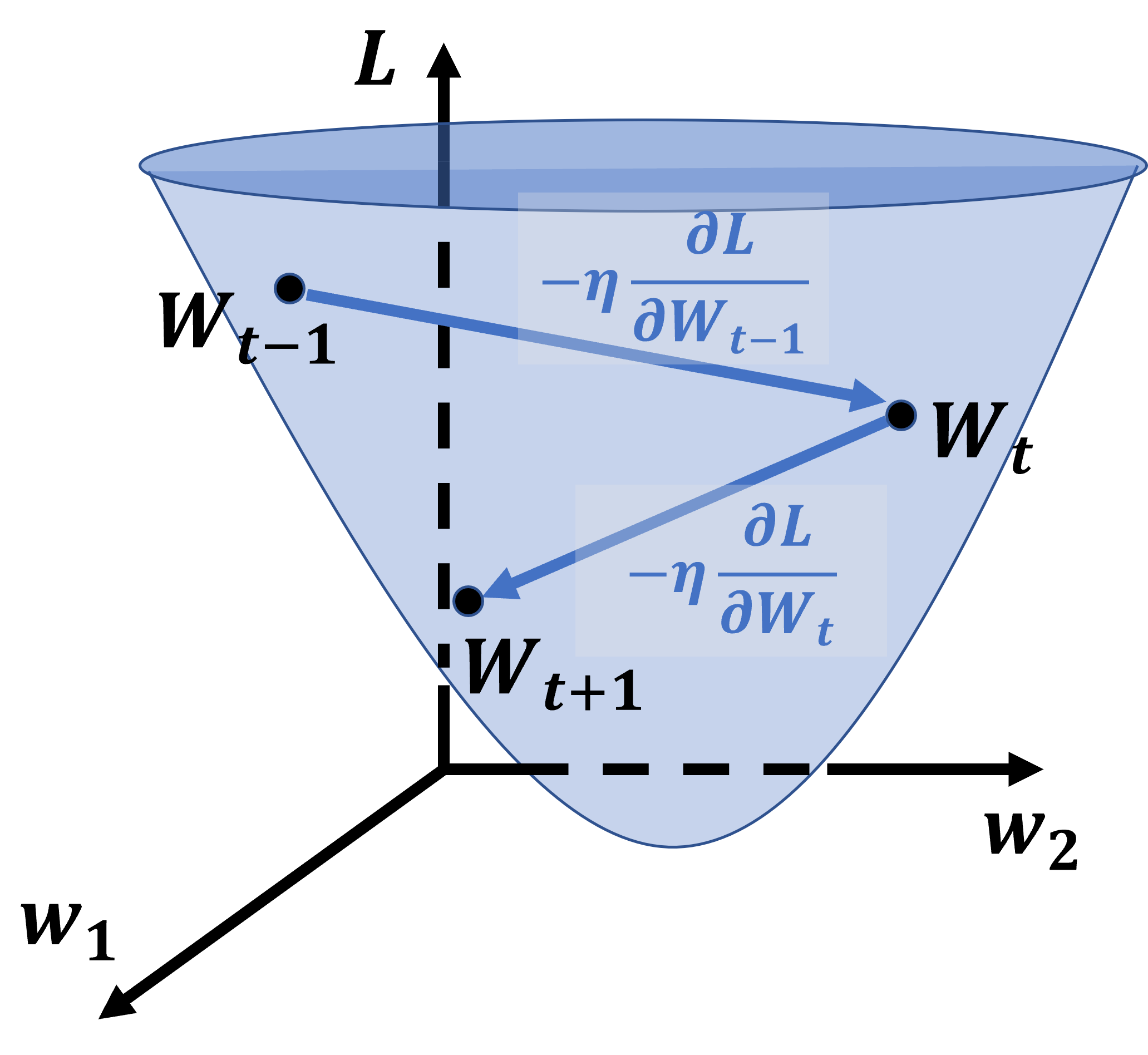
重み\(\mathbf{W}\)は、ベクトルである。すなわち、\(\mathbf{W}\)の関数である損失関数\(L\)は通常、多変数関数である。ここで、\(\mathbf{W} = (w_1, w_2)\)であるとする。この時、\(t-1, t, t+1, …\)と学習が進んでいく様子のイメージは、下図のようになる。
コード例
class SGD:
def __init__(self, lr=0.01):
"""
lr : learning rate(学習係数)
"""
self.lr = lr
def update(self, params, grads):
"""
重みの更新
"""
for key in params.keys():
params[key] -= self.lr * grads[key]\(L = \frac{x^2}{20} + 2y^2)\、すなわち唯一つの極小値(最小値)をもつ損失関数を使って、上での説明をシミュレーションしてみると、以下のようになる。
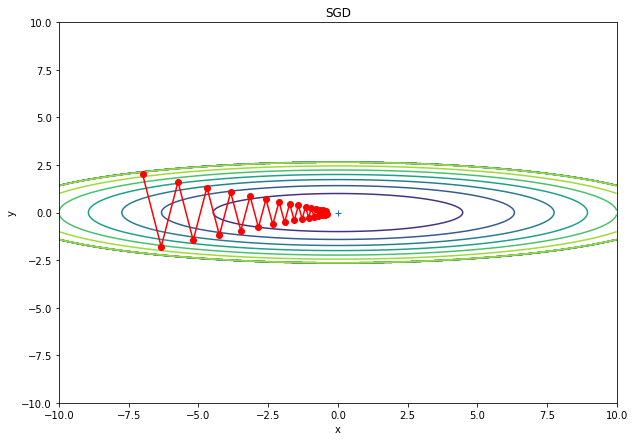
ジグザグとした挙動を確認できる。
Momentum
SGDでは、
「学習の各段階において、勾配が最も急な方向に重みベクトルを更新していく」
ため、学習の初期には、最も早く損失関数の谷底へ向かうことができる。
しかし、学習が進むと、勾配の小さい地点にもかかわらず、重みの更新量が大きすぎることにより、
「谷底(最小値)付近で、振動が起こり、谷底になかなかたどり着くことができない」
という問題が発生してしまう。
「細いパイプにピンポン球を投げ込むと、内面で何度も跳ね返ってしまい、なかなかパイプの底にたどり着かない」というイメージだ。
一方、Momentumでは、ボールを転がしたような挙動をさせることができ、このような振動を抑えることができる。
更新式
\begin{align*}
& \mathbf{v}_{t+1} = \alpha\mathbf{v}_t – \eta\frac{\partial L}{\partial \mathbf{W}_t}\\
& \mathbf{W}_{t+1} = \mathbf{W}_t \ + \ \mathbf{v}_{t+1}\\
& \mathbf{W}_t \ : \ パラメータ(重み)\\
& L \ : \ 損失関数\\
& \eta \ : \ 学習係数(正の値)
& \alpha \ (0 \ \le \ \alpha \ < \ 1)
\end{align*}
ここで、\(\mathbf{v}\)というベクトルは、勾配由来の\(-\eta\frac{\partial L}{\partial \mathbf{W}_t}\)という力を受けて、時間を経るごとに加速していくので、物理学での「速度」に対応する。なお、勾配のみを考慮すれば(右辺第1項を無視すれば)、更新式はSDGと全く同じものとなる。
しかし、Momentunでは、\(\alpha\mathbf{v}_t\)すなわち、「現在の速度に0以上1未満の係数をかけたもの」を、次の時刻の速度に足し合わせる。これは、物理学で言う”慣性“の導入に相当する。
慣性を導入すると、何が起こるか。
・現在の速度が大きいとき、外力を受けない限り、次の時刻における速度も大きいままである。
・現在の速度が小さいとき、外力を受けない限り、次の時刻における速度も小さいままである。
外力とは、今は勾配のことを指しているから、次のように言い換えることができる。
・勾配が大きいとき、次の時刻における速度も大きい。
・勾配が小さいとき、次の時刻における速度も小さい。
これは、非常に好都合ではないだろうか。
・学習の初期段階
→谷底から遠く、勾配が大きい場所では重みの更新量が大きくなる=学習速度が向上する。
・学習がある程度進んだ段階
→谷底付近では勾配が小さいので、重みの更新量が小さくなる=学習が収束しやすい。
数式ではイメージしづらいので、模式図を使って確認してみよう。
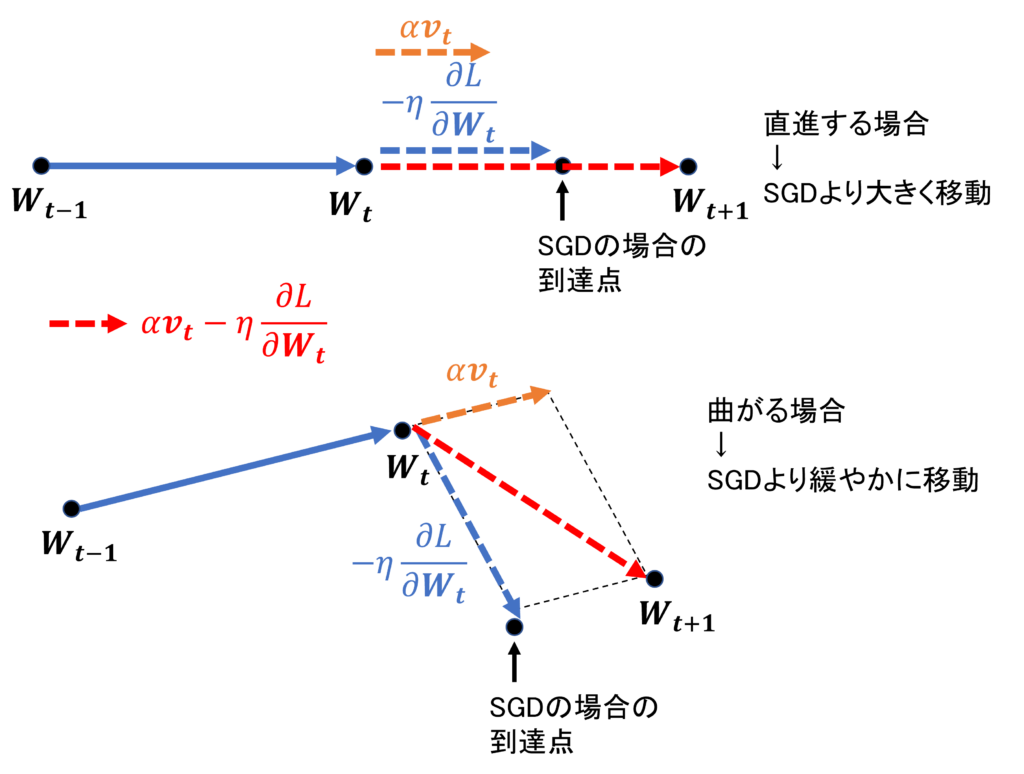
まず、上の図より、直進するような更新の場合、SGDよりも大きく更新できる。それにもかかわらず、
勾配が小さくなってくれば、\(\alpha\mathbf{v}_t\)も小さくなっていくので、学習が収束しやすい。また、このような力学的な項を取り入れたことで、「ジグザクとした振動」が軽減され、まるでボールが滑らかに坂を下るような挙動を示すようになる。
たった1工夫で、SGDとの違いがこれほど生まれるとは興味深い。
コード例
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
"""
lr : learning rate(学習係数)
momentm : モーメンタム係数
"""
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
"""
重みの更新
"""
if self.v is None:
"""
更新初回にインスタンス変数vを生成
"""
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]SGDの時と同じ関数で学習時の挙動を確認してみると、確かに更新の仕方が滑らかになっている。
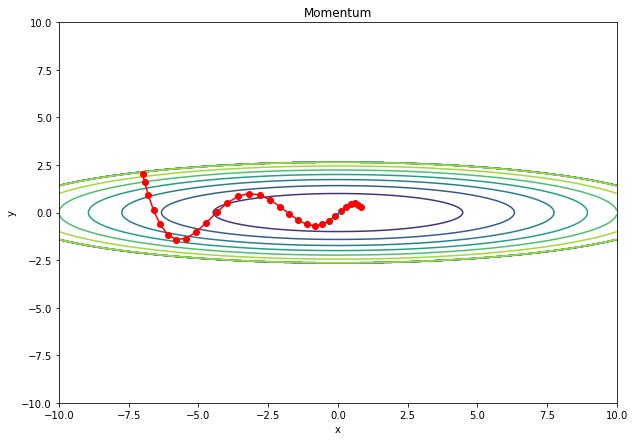
メモ:Momentumを改善した手法として、Nesterov Acceletate Gradientが存在する。
AdaGrad
Momentumでは、慣性の導入によって、初期の学習を加速させ、かつ、学習を滑らかにする工夫がなされた。
一方、学習方法の工夫をする手段がもう一つある。
「学習が進むにつれて、学習係数を小さくしていく」というアイデアである。
そのアルゴリズムが、AdaGradである。
更新式
\begin{align*}
& \mathbf{h}_{t+1} = \mathbf{h}_t \ + \ \frac{\partial L}{\partial \mathbf{W}_t}\odot\frac{\partial L}{\partial \mathbf{W}_t}\\
& \mathbf{W}_{t+1} = \mathbf{W}_t \ – \ \eta\frac{1}{\varepsilon + \sqrt{\mathbf{h}_{t+1}}}\odot\frac{\partial L}{\partial \mathbf{W}_t}
\end{align*}
勾配ベクトルの自乗(アダマール積)\(\frac{\partial L}{\partial \mathbf{W}_t}\odot\frac{\partial L}{\partial \mathbf{W}_t}\)の各成分は、必ず正の値をとる。よって、\(\mathbf{h}_t \)ベクトルの各成分は、常に正の値をとる。
アダマール積の例
$$
\left(
\begin{array}{c}
a_1 \\
a_2 \\
\vdots \\
a_n
\end{array}
\right)
\odot\left(
\begin{array}{c}
a_1 \\
a_2 \\
\vdots \\
a_n
\end{array}
\right) = \left(
\begin{array}{c}
a_1^2 \\
a_2^2 \\
\vdots \\
a_n^2
\end{array}
\right)$$
※内積:(\(n\)次元のベクトル) \(\cdot\)(\(n\)次元のベクトル) = スカラー量
アダマール積:(\(n\)次元のベクトル) \(\cdot\)(\(n\)次元のベクトル) = (\(n\)次元のベクトル)
更新式における\( \eta\frac{1}{\varepsilon + \sqrt{\mathbf{h}_{t+1}}}\)は、学習係数の役割を果たしている。つまり、”見かけの係数“である。
※\(\mathbf{h}\)はベクトルである。\(\mathbf{W}\)の要素と同じ数、\(\mathbf{h}\)も要素を持っている。SGDやMomentumでは学習率\(\eta\)は、たった1つの定数によって定まっていた。しかし、AdaGradでは、重み\(\mathbf{W}\)のそれぞれの成分に対応した”見かけの学習係数”が存在することになる。
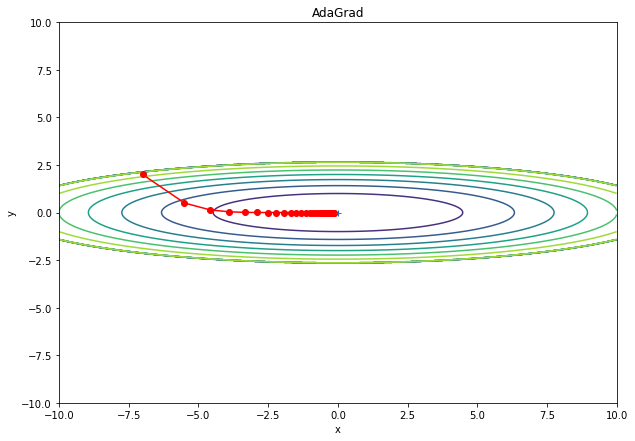
AdaGradには、
・パラメータごとに”見かけの学習率”を設定できる。
・学習が進むにつれて、見かけの学習率は単調減衰していく。
という利点がある。しかし、見かけの学習率は「単調減少しかしない」という課題がある。
鞍点のような停留点(プラトー)に達したとき、抜け出しにくくなってしまう。
コード例
class AdaGrad:
def __init__(self, lr=0.01):
"""
lr : learning rate(学習係数)
"""
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
"""
更新初回にインスタンス変数hを生成
"""
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
# epsilon = 1e-7を分母に加えることを留意
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)シミュレーション例。更新量が、単調減少している様子を確認できる。
RMSProp
AdaGradに”移動平均”を導入する。まず、更新式を見てみる。
更新式
\begin{align*}
& \mathbf{h}_{t+1} = \rho\mathbf{h}_t \ + \ (1-\rho)\frac{\partial L}{\partial \mathbf{W}_t}\odot\frac{\partial L}{\partial \mathbf{W}_t}\\
& \mathbf{W}_{t+1} = \mathbf{W}_t \ – \ \eta\frac{1}{\varepsilon + \sqrt{\mathbf{h}_{t+1}}}\odot\frac{\partial L}{\partial \mathbf{W}_t}
\end{align*}
移動平均(指数平滑化移動平均):
減衰率\(\rho\)の割合で\(\frac{\partial L}{\partial \mathbf{W}_t}\odot\frac{\partial L}{\partial \mathbf{W}_t}\)を足し合わせながら\(\mathbf{h}\)を更新していくことで、過去の情報が指数関数的に薄まっていく。
過去の情報が薄まっていく理由は以下のように説明できる。数式が煩雑になるので、勾配ベクトルを\(\frac{\partial L}{\partial \mathbf{W}_t} = \mathbf{g})とおく。(gはgradientの意味)
RMSPropの更新式は、次のように変形すると、時刻\(t-1\)の項を使って表すことができる。
\begin{align*}
\mathbf{h}_{t+1} &= \rho\mathbf{h}_t \ + \ (1-\rho)\mathbf{g}\odot\mathbf{g}_t\\
&= \rho{ \ \rho\mathbf{h}_{t-1} \ + \ (1-\rho)\mathbf{g}_{t-1}\odot\mathbf{g}_{t-1} \ } \ + \ (1-\rho)\mathbf{g}\odot\mathbf{g}_t
\end{align*}
2行目の式では、過去の情報、すなわち{}で括られた時刻\(t-1\)の項には、\(\rho\)がかかっていることが分かる。一方、現在の情報、すなわち時刻\(t\)の項には、それがない。
2行目の式中の\(\mathbf{h}_{t-1} \)は、さらに時刻\(t-2\)の情報を用いて表すことができる。そして、時刻\(t-2\)の項には、二重で\(\rho\)がかかる。
したがって、古い時刻の情報ほど、減衰率\(\rho\)が何重にもかかる。
このようにして、過去の情報が指数関数的に薄まっていくという訳である。
RMSpropのメリット
過去の情報が薄まり、現在時刻の情報の重みが相対的に大きくなることのメリットは何だろうか。
それは、勾配の小さい領域、すなわち停留点にとどまったとき、次第に\(\mathbf{h}\)が小さくなっていくので、見かけの学習率が増加し、プラトーを抜け出しやすくなることである。
これによって、「見かけの学習率が単調にしか減少しないため、プラトーを抜け出せなくなる」というAdaGradの弱点を克服できる。
コード例
class RMSprop:
def __init__(self, lr=0.01, decay_rate = 0.99):
"""
lr : learning rate(学習係数)
secay_rate : 減衰率
"""
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
"""
更新初回にインスタンス変数hを生成
"""
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
# epsilon = 1e-7を分母に加えることを留意
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
Adam
Adamは、RMSProp × Momentum のような最適化手法である。
Momentumは、力学的な”慣性”の概念を取り入れることで、学習を加速・安定化させる手法だった。
RMSPropは、学習の経過とともに減衰する“見かけの学習率”を導入したAdaGradに、過去の情報を減衰させる”移動平均”の概念を加えることで、プラトーから脱出しやすい手法だった。
更新式
\begin{align*}
&\mathbf{m}_{t+1} = \beta_1\mathbf{m}_t \ + \ (1-\beta_1)\frac{\partial L}{\partial \mathbf{W}_t} \ : \ 1次モーメント(勾配の移動平均)\\
&\mathbf{v}_{t+1} = \beta_2\mathbf{m}_t \ + \ (1-\beta_2)\frac{\partial L}{\partial \mathbf{W}_t}\odot\frac{\partial L}{\partial \mathbf{W}_t} \ : \ 2次モーメント(勾配の2乗の移動平均)\\
& \\
&\hat{\mathbf{m}}_{t+1} = \frac{\mathbf{m}_{t+1}}{1 – \beta_1^t}\\
&\hat{\mathbf{v}}_{t+1} = \frac{\mathbf{v}_{t+1}}{1 – \beta_2^t}\\
& \\
&\mathbf{W}_{t+1} = \mathbf{W}_t \ – \eta\frac{1}{ \sqrt{\hat{\mathbf{v}}_{t+1}} + \varepsilon}\odot\hat{\mathbf{m}_{t+1}}
\end{align*}
先に、Adamで初めて登場した「バイアス補正」(第3式、第4式)について見てみよう。
学習が進むにつれて、\(\beta_1^t\)が0に近づき、右辺の分母の値が1に漸近していくことが分かる。右辺の分母が1ならば、第3式、第4式は意味を成していないことになる。
移動平均によって、学習の初期においては、
・学習初期の\(\mathbf{m}\)が小さく見積もられる。
・学習初期の\(\mathbf{v}\)が小さく見積もられる。
という「バイアス」がかかってしまう。
一方、学習の初期には、右辺の分母を1より小さくする効果をもたらす。これにより、
・学習初期の”見かけの勾配”\(\hat{\mathbf{m}}\)を大きくできる。
・学習初期の”見かけの学習率”\(\hat{\mathbf{m}}\)を小さくできる。
重み\(\mathbf{W}\)の更新式を見ると、これまでの手法とは違い、勾配が入っていないように見える。
しかし、勾配に移動平均を取り入れた\(\hat{\mathbf{m}}\)が、”見かけの勾配“としての役割を果たしている。また、”見かけの学習率”\(\hat{\mathbf{v}}\)にも移動平均が導入されているが、こちらはRMSPropでの\(\mathbf{h}\)の更新式と全く同じである。
コード例
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
"""
lr : learning rate(学習係数)
beta1, beta2 : 減衰率
m : 1次のモーメント
v : 2次のモーメント
"""
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
"""
更新初回にインスタンス変数 m, vを生成
"""
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
"""
モーメントのバイアス補正
"""
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
# epsilon = 1e-7を分母に加えることを留意
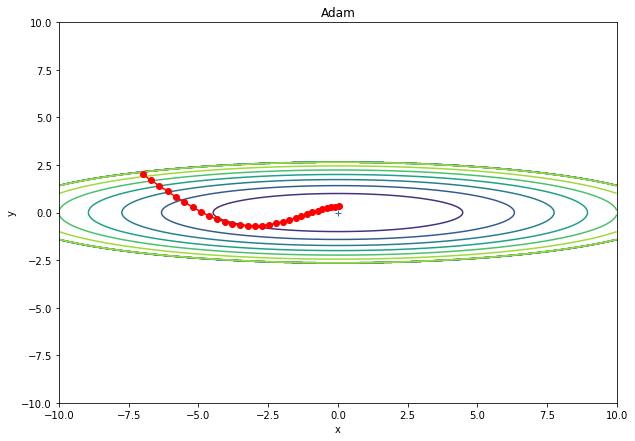
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)シミュレーション例。Momentumと挙動が似ているが、より早く学習が進んでいる。
参考資料:
「ゼロから作るDeepLearning」斎藤康毅
Diederik Kingma and Jimmy Ba. (2014) Adam: A Method for Stochastic Optimization.


コメント