通常の透過光観察では見えない凹凸構造を可視化する。そんな顕微鏡の話である。
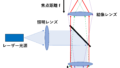
微分干渉顕微鏡の概観~段差を検出する~
高さ h の段差をもつサンプルがあるとする。
平面波の入射光をサンプルに照射すると、反射光には最大で 2h の”光路差”(屈折率、透過した物体の厚さ、凹凸などの違いによって、通過した光が進んだ距離に差が生まれること)が生じる。
この光路差を利用したのが「微分干渉顕微鏡(Differrential Interference Contrast ; DIC)」である。DICは、h = 数nmの段差を検出することができる。

ここで、疑問が生じる。
“光路差”を利用するとは言っても、DICはいったいどうやって光路差を検出するのだろうか。
ノマルスキープリズム~入射光を2種類の光に分ける~
ここで、重要な役割を果たす「ノマルスキープリズム(Nomarski prism)※」について解説する。
まず、光源から、一方向に振動する光(偏光)が入射する。
詳細は下で説明するが、実際の装置でもそのような系になっているのでご安心を。
ノマルスキープリズムに入射した偏光は、互いに直交する振動方向を持つ2つの偏光に分けられる。この2つの偏光はE光(Extraordinary light)とO光(Ordinary light)と呼ばれる。
下の図で、青の両矢印はO光の振動方向、〇の中に+の赤い記号はE光の振動方向(画面に垂直な方向)を表している。つまり、2つの偏光の振動方向を表現している。
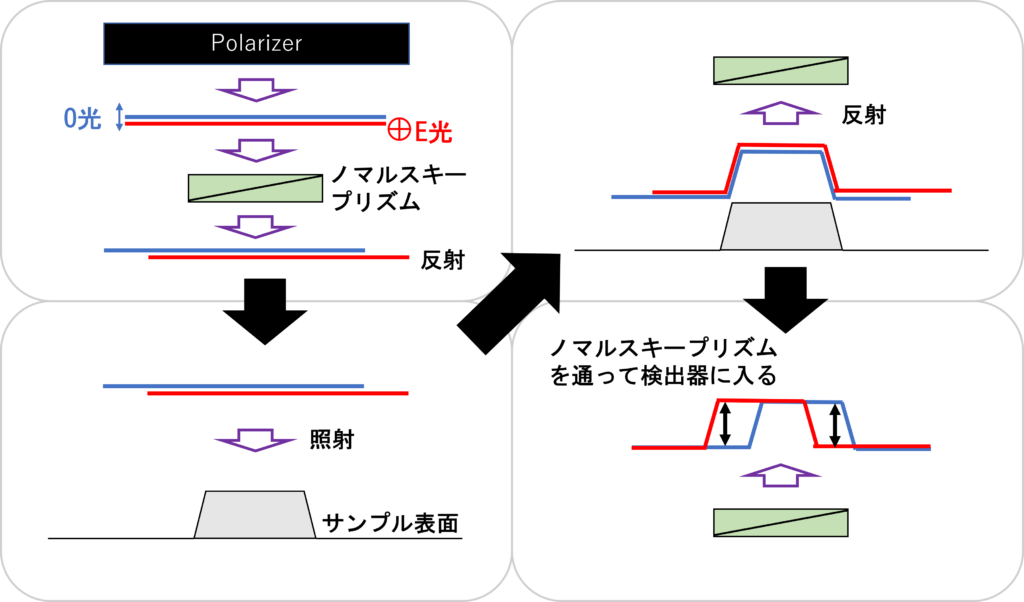
※「ウォラストンプリズム(Wollaston prism)」も同じような性質を持つ。
ここで、2つの偏光の差分が0でない場所は、光路差、すなわち段差(の斜面)の存在を反映している。
アナライザー~2つの偏光の引き算を実現する~
では、E光とO光の光路差の引き算は、どうすれば実現できるだろうか。
単純に引き算をすればよさそうだが、E光とO光は互いに直交する偏光であるから、相互作用をすることができない。つまり、直接引き算をすることはできないのである。
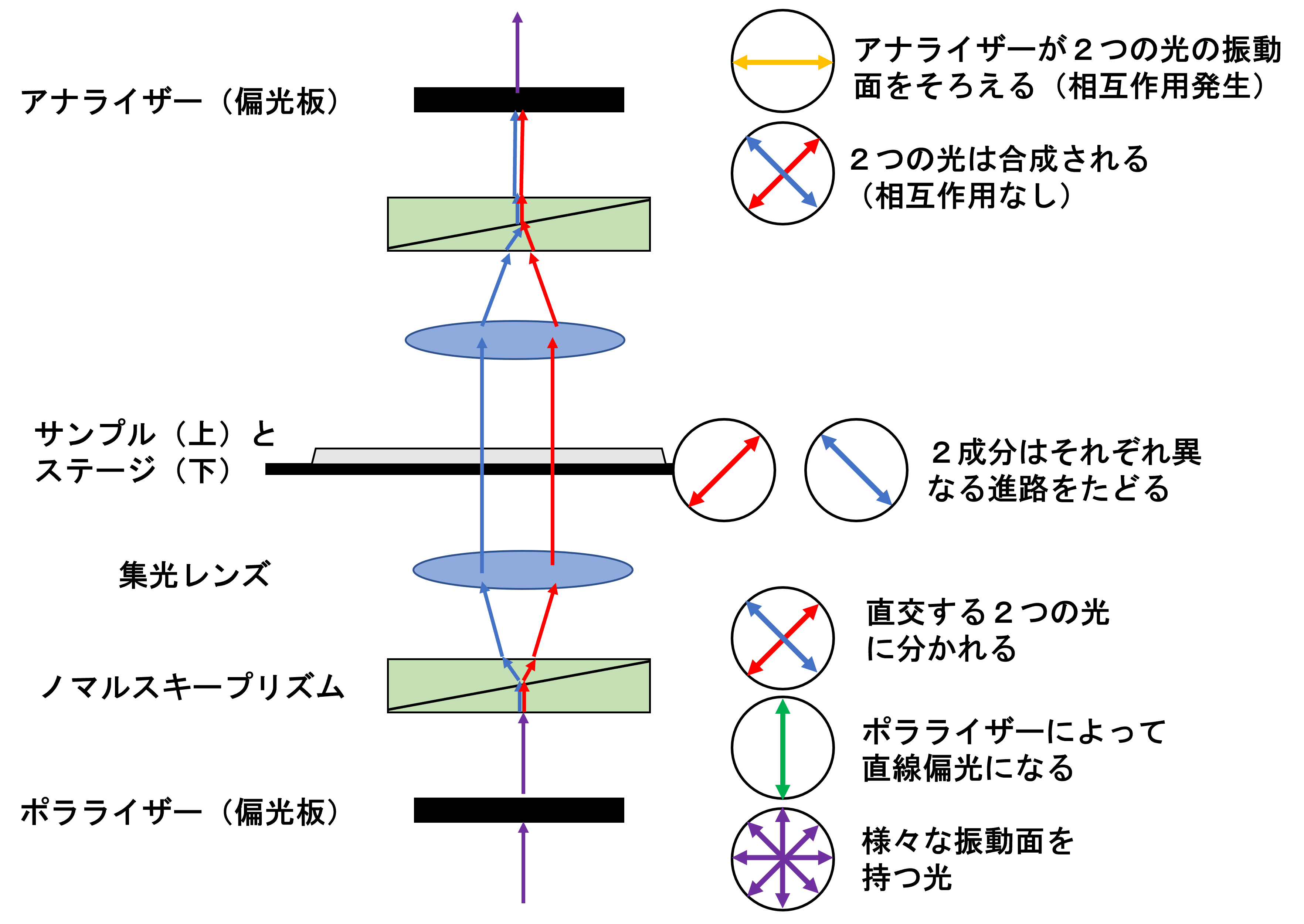
ここで登場するのがアナライザー(Analyzer)※であり、2種類の互いに垂直な振動面を持った偏光を、1つの振動面を持った偏光に変換させて、相互作用(干渉)させることで引き算を可能にする。
※アナライザーとポラライザーは、偏光面の方向が直交しているだけで、機能は全く同じである。
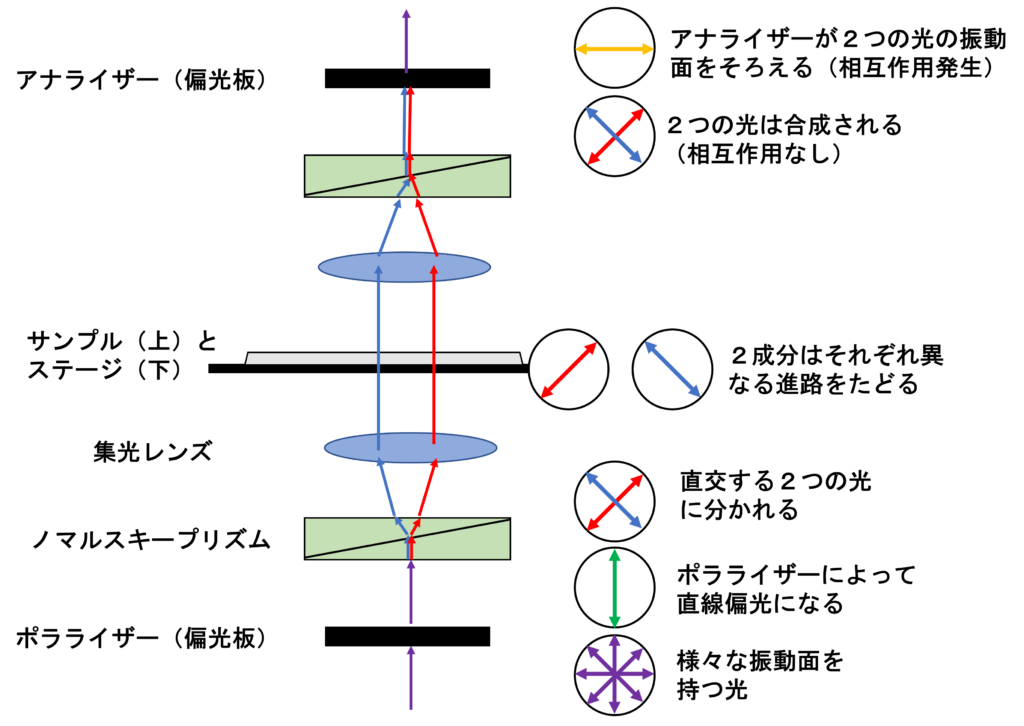
なお、ここではシンプルな図解のために「透過型」(光がサンプルを透過し、厚みの変化を検出する)の微分干渉顕微鏡の原理を示した。「反射型」(光がサンプル表面で反射し、凹凸の斜面を検出する)と原理は同じである。
どちらも、
「E光とO光の(光路差に由来する)干渉によって、厚みの変化や凹凸の斜面がコントラストとして検出される」
という共通した原理である。
微分干渉~小さな段差の斜面がコントラストとして可視化できる~
段差の存在する場所に偏光が照射されると、E光とO光の光路差が発生し、干渉が発生する。
一方、高さに変化のない場所に偏光が照射されると、E光とO光の光路差がないために干渉が起きない。
これらの結果、下の図のように、段差のある場所にだけコントラストが見える。
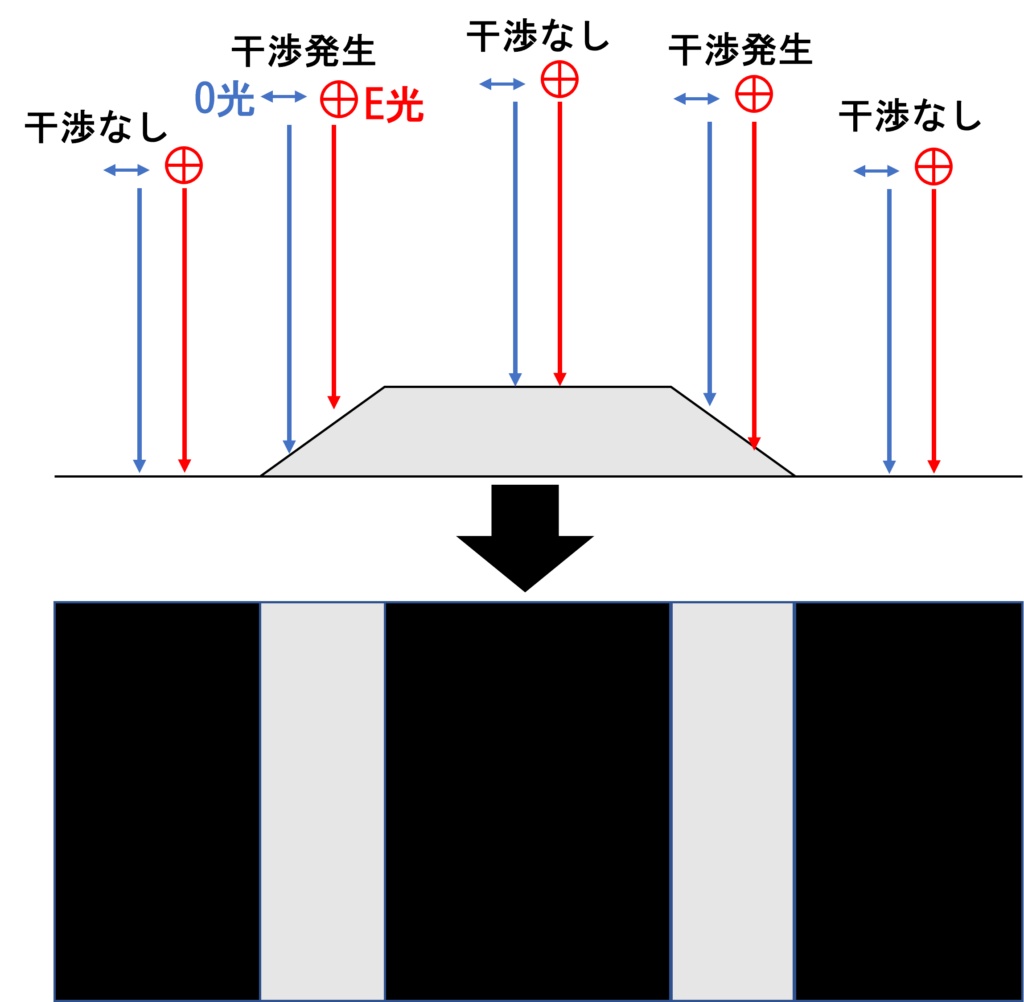
ちなみに、平坦な箇所に当たった2つの光にはほとんど光路差が生まれない。微分干渉とは、すなわちE光とO光の引き算であるから、この場合、平坦な箇所はほぼ真っ暗になってしまうのである。
また、コントラストの色は斜面の傾きの絶対値を反映しているので、右肩下がりの斜面なのか、右肩上がりの斜面なのかを判別することはできない。
しかし、ノマルスキープリズムの位置を少しずらすことで、この問題を解決することができる。
詳しくは、今後の記事で書く機会があるかもしれない。
最後の疑問~微分干渉顕微鏡の高さ方向の分解能に限界はあるのか~
微分干渉顕微鏡は、2つの偏光の光路差を利用した顕微鏡であり、結晶表面での数ナノメートルの段差を可視化している例もある。では、微分干渉顕微鏡の高さ方向に限界はあるのだろうか。
答えは、「原理的には限界がないが、可視化できるかは別問題」である。
というのも、段差が小さいほど平坦な箇所との差がなくなり、上の灰色で示したコントラストは、段々と黒に近づいていくためである。つまり、原子レベルのサイズの段差を可視化しようとすると、ほぼ同じ光の強度を持ったコントラストを、見分ける必要がある。したがって、ノイズの除去、入射光や反射光のロスをなくす、コントラストを強調する技術を用いるなどの対策が必要である。
したがって、技術的な問題をクリアできれば、微分干渉顕微鏡の高さ方向の分解能には、限界がないといえる

コメント