【二分探索（応用編）】最大値の最小化・最小値の最大化問題を解く（Python）

アルゴリズムの実装の勉強をしていると、C++などの実装例はWeb上、書籍など豊富に存在するが、Pythonで解説したものは少ないように感じている。本記事では、競技プログラミングなどにおいて、理解が詰まりやすい問題について、Pythonでの実装例を紹介している。

1. 二分探索を応用するための条件

二分探索のコンセプトや、基礎的な二分探索の問題については、
【二分探索（基礎編）】値の探索、境界値・範囲を求める（Python）
で解説している。

やや複雑な問題を、二分探索を応用して解くためには、扱っている問題に「単調性」を見出せる必要がある。単調性とは、ある条件\(C\)Conditionの略)に対して、

値\(x\)が条件\(C\)を満たす場合、\(y\le x\)を満たすすべての\(y\)も条件\(C\)を満たす。
または
値\(x\)が条件\(C\)を満たす場合、\(y\ge x\)を満たすすべての\(y\)も条件\(C\)を満たす。

などと一般化して表現することができる。ここで不等号に=が含まれるか否かは問題によるので、必ずしも上記の２つだけが「単調性」ではない。細かいことはさておき、とにかく

• 問題で扱う配列が単調増加（減少）である。
• 配列の各要素の順番を入れ替えても良い場合、配列をソートする。

このような状況下に持ち込めば、二分探索を使える場合が少なくない。

2. 複数のパイプから同じ長さのパイプを切り出すとき、長さの限界は？

\(n\) 本のパイプがあり、長さはそれぞれ \(A_1, A_2, …, A_n\) です。今、\(n\)本のパイプから \(k\) 本の同じ長さのパイプを切り出すことを考えます。パイプを切って分割することはできますが、つなげることはできません。パイプの切り方を工夫した結果、切り出すことができるパイプの長さの最大値を答えてください。

引用元：https://paiza.jp/works/mondai/binary_search/binary_search__application_step0

考え方

この問題はそれほど複雑ではないので、「単調性」をそれほど意識する必要はない。

二分探索により、切り出せる/切り出せない長さの境界を求めていきたい。長さは小数となる可能性もあるため、探索範囲の中央値は「２で割った商」ではなく「２で割った値そのもの」となる。この点を除けば、【二分探索（基礎編）】値の探索、境界値・範囲を求める（Python）で解説したものと全く同じ考え方である。

コード例

n, k = map(int, input().split())
A = list(map(int, input().split()))

left = 0.0
right = 10001.0
for i in range(100):
    num_of_pipes = 0
    mid = (left + right)/2
    # 作れるパイプの数を数える
    for a in A:
        num_of_pipes += a // mid # 本数は整数である必要がある
    if num_of_pipes < k: # k本切り出せない場合、探索範囲を、１本あたりの長さが小さいほうに絞る
        right = mid 
    else: # k本以上切り出せる場合、探索範囲を、１本あたりの長さが大きいほうに絞る
        left = mid
print(mid)

3. 単位価値（平均価値）の最大化

博物館に、\(n\) 個の財宝が展示されています。各財宝の価値は \(V_1, V_2, …, V_n\) であり、重さは \(W_1, W_2, …, W_n\) です。怪盗であるあなたは、paiza 博物館からちょうど \(k\) 個の財宝を盗み出そうとしています。
\(k\) 個の財宝の平均価値を、(\(k\) 個の財宝の価値の和) ÷ (\(k\) 個の財宝の重さの和) で定義します。
盗み出す財宝を適切に選んだ結果、平均価値が最大でいくつになるかを答えてください。

引用元：https://paiza.jp/works/mondai/binary_search/binary_search__application_step1

考え方

問題がやや複雑なので、「単調性」を上手く使っていく必要がある。

まず、条件\(C(x)\)を、「\((平均価値) \ge x\)となる選び方が存在する」と設定する。
そして、この条件を数式で表すと、次のようになる。

$$\frac{\sum_{i \ in S_k}V_i}{\sum_{i \ in S_k}W_i} \ge x$$

ここで、集合\(S_k\)は、全\(n\)個の中から取り出した\(k\)個の要素を表す。上記の条件式を変形すると、次のように書き換えることができる。

$$\sum_{i \ in S_k}(V_i – x*X_i) \ge 0$$

また、\(S_k\)は\((V_i – x*X_i)\)のなるべく大きいものを取ったほうが条件を満たしやすい。したがって、実装する際には\((V_i – x*X_i)\)の大きい順に並べたリストを作成し、大きいほうから\(k\)個を取り出すのが良い。

コード例

n, k = map(int, input().split())
W = list(map(int, input().split()))
V = list(map(int, input().split()))

def is_ok(x):
    # 単位価値がx以上となる選び方は存在するか？
    VXW = [vi - x * wi for vi, wi in zip(V, W)]
    # 降順に並べ替える
    VXW.sort(reverse=True)
    return sum(VXW[:k]) >= 0

def binary_search(ng, ok):
    while (abs(ok - ng) > 10**-9):  # 絶対誤差小数8桁程度
        mid = (ok + ng) / 2 # 少数を含むので//でなくて良い
        if is_ok(mid):
            ok = mid
        else:
            ng = mid
    return ok

print(binary_search(10**6 + 1, 0))

参考にした記事：平均最大化についての問題解説

4. 最小値の最大化

長さ \(L\) [cm] の太巻きがあり、これを \(n\) 人で分けようとしています。太巻きにはあらかじめ \(k\) 個の切れ目が入っており、\(i\) 個目の切れ目は左端から \(A_i\) [cm] のところに入っています。あなたは、切れ目を \(n-1\) 個選んでそこで切ることにより、太巻きを \(n\) 分割しようとしています。\(n\) 人はみなお腹がすいているので、なるべくたくさん食べたいと思っています。切れ目の選び方を工夫したとき、最も短い太巻きの長さを最大でいくつにできるかを答えてください。

引用元：https://paiza.jp/works/mondai/binary_search/binary_search__application_step2

考え方

条件\(C(x)\)を、「最も短い太巻きの長さが\(x\)となる\(n\)分割の仕方が存在するが存在する」と設定する。

ここで、１つの例を考える。まず、長さ23cmの太巻きと、切れ目を格納したリスト\(A={2,6,9,10,12,15,19,23}\)があり、これを\(n=5\)分割することを考える。

\(x = 4\)のとき、条件\(C(x=4)\)は「最も短い太巻きの長さが\(x=4\)となる\(n=5\)分割の仕方が存在する」である。

では、条件\(C(x=4)\)の判定はどうすれば良いだろうか。\(x\)を超える範囲で、なるべく短く切り取っていき、\(n\)個以上の要素ができればよい。下の図では、太巻き左端を0 [cm]、右端を23 [cm]として、切れ目の位置を数直線上に表している。

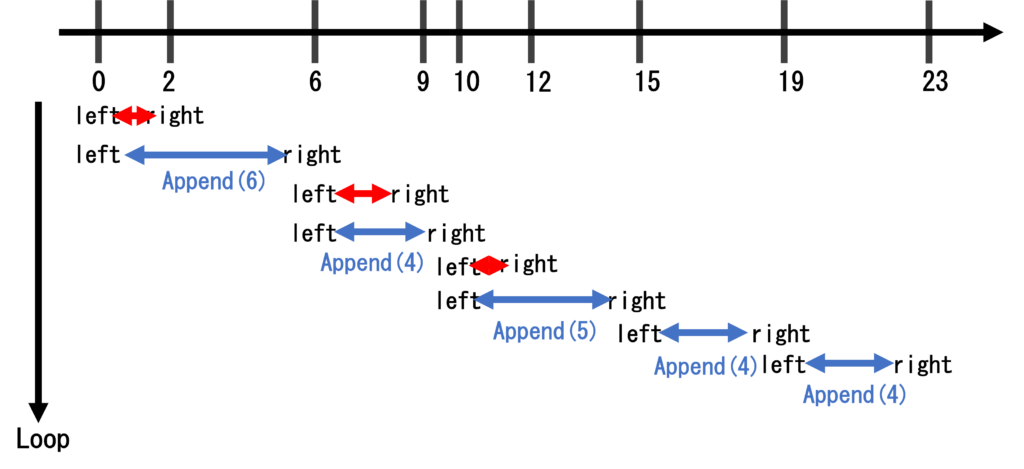
leftとrightの差が4以上になったとき、位置に包丁を入れていく（Appendで切り取ったものを空のリストAAに格納していく）イメージである。

下に行くにつれて、ループを回していることに相当する。

１番目のループでは、長さが2なので、未だ切り取ることができない。2番目のループでrightを１つ右にずらすと、長さ6（長さ４以上を満たす）の太巻きを切り取ることができる。
→リストAAに切り取った長さ6を格納

３番目のループでは、まず左端が6の位置に移動していることに注意したい。これは、１つ前のループで、太巻きを切り取ったためである。rightとleftの差より、長さ4以上を切り取ることができない。
４番目のループでrightを１つ右にずらすと、長さ４（長さ４以上を満たす）の太巻きを切り取ることができる。
→リストAAに切り取った長さ4を格納

これを繰り返していくと、AA=[6, 4, 5, 4, 4]となる。AAの長さは5であるから、条件\(C(x=4)\)「最も短い太巻きの長さが\(x=4\)となる\(n=5\)分割の仕方が存在する」を満たしている。

後は、条件\(C(x)\)を満たす/満たさない\(x\)の境界を二分探索で探せばよい。

コード例

L, n, k = map(int, input().split())
A = [0] + list(map(int, input().split()))
A.append(L)

def is_ok(x):
    # 最小値がx以上となる選び方は存在するか？
    l = 0
    r = 1
    AA = []
    while r < k+2:
        if A[r] - A[l] >= x:
            AA.append(A[r] - A[l])
            l = r
            r += 1
        else:
            r += 1
        
    return len(AA)>=n

def binary_sort(left, right):
    while right - left > 1:
        mid = (left + right)//2
        if is_ok(mid):
            left = mid
        else:
            right = mid
    return left
    
binary_sort(0, 10**9+1)

最大値の最小化

長さ \(L\) [cm] の太巻きがあり、これを \(n\) 人で分けようとしています。太巻きにはあらかじめ \(k\) 個の切れ目が入っており、\(i\) 個目の切れ目は左端から \(A_i\) [cm] のところに入っています。あなたは、切れ目を \(n-1\) 個選んでそこで切ることにより、太巻きを \(n\) 分割しようとしています。\(n\) 人はみなお腹がいっぱいなので、なるべく少なく食べたいと思っています。切れ目の選び方を工夫したとき、最も長い太巻きの長さを最小でいくつにできるかを答えてください。

引用元：https://paiza.jp/works/mondai/binary_search/binary_search__application_step3

考え方

「最小値の最大化」で図解したのと同じ要領である。

\(x\)を超えない範囲で、左端からなるべく長く切り取っていき、\(n\)個以下の要素ができればよい。

コード例

L, n, k = map(int, input().split())
A = [0] + list(map(int, input().split()))
A.append(L)
def is_ok(x):
    # 最大値がx以下となる選び方は存在するか？
    l = 0
    r = 1
    AA = []
    while r < k+2:
        # Trueの可能性が無い時点で終了
        if A[r] - A[l] > x:
            return False
        # できる限り長くしていく
        #☆この条件が逆に並んでいると、list outof indexとなってしまう。
        while (r < k+2) and (A[r] - A[l] <= x):
            r += 1
        # ループが止まったらリストに加える
        AA.append(A[r-1] - A[l])
        l = r -1 
    return len(AA) <= n

def binary_sort(left, right):
    while right - left > 1:
        mid = (left + right)//2
        if is_ok(mid):
            right = mid
        else:
            left = mid
    return right
    
print(binary_sort(0, 10**9+1))

5. ２つの数列の「各要素の差分の絶対値」の中から、効率的に境界を見つける

数列 \(A = (A_1, A_2, …, A_n)\) と数列 \(B = (B_1, B_2, …, B_m)\) が与えられます。
これらの数列を用いて、\(n\) 行 \(m\) 列のマス目に数を書き込むことを考えます。具体的には、\(i\) 行 \(j\) 列目\((1 \le i \le n, 1 \le j \le m)\) に \(|A_i – B_j|\) を書き込みます。表に書き込まれる数は全部で \(n*m\) 個ありますが、それらを小さいほうから並べたとき \(k\) 番目にくる値を求めてください。

引用元：https://paiza.jp/works/mondai/binary_search/binary_search__application_boss

考え方

全要素数n*mの最大値は30,000*30,000であるから、これをソートするのは現実的ではない。かといって、O(n)の計算量で収まるような画期的な方法も思いつかない。

ここで、数列Aの各要素\(A_i\)に対し、\(|A_i – B_j| \le k\)を満たすような要素の数を数え上げ、それらの総和を足していくことを考える。そして、「数え上げ」を二分探索で行うことができれば、O(n*logm)の計算量に収めることができる。そのために必要な処理は

• 数列Bをソートしておく。
• \(|A_i – B_j| \le x\)を、絶対値の無い形の条件式に書き換える。

である。後者については、【二分探索（基礎編）】値の探索、境界値・範囲を求める（Python）で解説している境界値の求め方を参考にされたい。

コード例

n = int(input())
A = list(map(int, input().split()))
m = int(input())
B = list(map(int, input().split()))
k = int(input())

"""
    A_i >= k を満たす最小の i を返す
    A_i >= k を満たす i が存在しない場合は n を返す
"""
def binary_search_low(A, n, k):
    # 探索範囲
    left = 0
    right = n
    
    # 探索範囲を狭めていく
    while left < right:
        # 探索範囲の中央
        mid = (left + right)//2
        
        if A[mid] < k:
            # a[0] ~ a[mid] は k 未満なので調べる必要が無い
            left = mid+1
        else:
            right = mid
    return left

"""
    A_i <= k を満たす最大の i を返す
    ==> (A_i > kを満たす最小のi) - 1
    A_i > k を満たす i が存在しない場合は(全てk以下) n を返す
"""
def binary_search_up(A, n, k):
    # 探索範囲
    left = 0
    right = n
    
    # 探索範囲を狭めていく
    while left < right:
        # 探索範囲の中央
        mid = (left + right)//2
        
        if A[mid] <= k:
            # a[0] ~ a[mid] は k 以下なので調べる必要が無い
            left = mid+1
        else:
            right = mid
    return right

B.sort()
left, right = 0, 200000001
while right - left > 1:
    mid = (left + right) // 2
    smaller = 0
    for i in range(n):
        # A[i]+mid以上となる境界
        # A[i]-mid未満となる境界
        smaller += binary_search_up(B, m, A[i]+mid) - binary_search_low(B, m, A[i]-mid)
    if smaller < k:
        left = mid
    else:
        right = mid
print(right)