アルゴリズムの実装の勉強をしていると、C++などの実装例はWeb上、書籍など豊富に存在するが、Pythonで解説したものは少ないように感じている。本記事では、競技プログラミングなどにおいて、理解が詰まりやすい問題について、Pythonでの実装例を紹介している。
1. 二分探索のコンセプト
二分探索の原理について詳しく解説している記事・書籍はいくらでもあるが、ここであえて言及するならば、二分探索は辞書で単語を探す過程と非常に似ている。
例えば、単語 “goal” を英和辞典で探したいとき、どうしたら効率的だろうか。
簡単に、Aから始まりZで終わる1000ページの辞書があるとしよう。
この時、”A” → “B” → “C” → “D” → “E” → “F” → “G” のように1つずつ追っていく必要はない。
例えば、辞書の真ん中あたり(だいたい500ページ目)を開いて、 “M” を見つけたならば、”G”は500ページ目より手前にあるはずなので、500~1000ページ目は無視して良い。
この時点で、探索範囲は 1~500ページ目、すなわち全ページ数の1/2になっている。
次に、残った1~500ページの真ん中あたり(大体250ページ目)を開いて “E” を見つけたならば、”G”は250ページ目より先にあるはずなので、1~250ページ目は無視して良い。
この時点で、探索範囲は 250~500ページ目、すなわち全ページ数の1/4になっている。
このように、残りの探索範囲の真ん中あたりを境に、探索範囲を約半分にする作業を繰り返していけば、目的の単語にたどり着ける。
辞書で単語を調べる際、私たちは無意識にこの作業を行っている。
このような、効率的な探索方法が、二分探索のコンセプトである。
2. 整数が昇順に並んだ配列の中から、指定された値を探索
問題
引用元:https://paiza.jp/works/mondai/binary_search/binary_search__basic_step0
ソートされた数列 \(A = (A_1, A_2, … A_n)\) と、\(q\) 個の整数 \(k_1, k_2, … k_q\) が与えられます。
各 \(k_i\) について、数列 \(A\) に含まれているなら “Yes” と、含まれていないなら “No” と出力してください。なお、\(A\) の要素数及び、\(n, q\) の最大値はいずれも 200,000 です。
考え方
上の引用元に分かりやすいヒントが記載されているので、ここでは、要素数11個を持つリストAの中から、指定された数k=11を探すことを、図を用いて考えてみる。
本問が理解できれば、以降の問題もスムーズに理解できるはずだ。
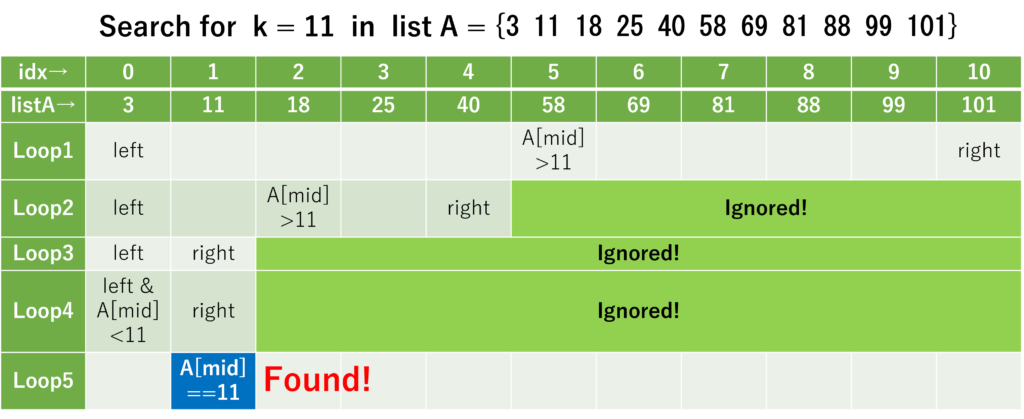
ループが進むごとに探索範囲が狭まっていき、5回のループでk=11という数字が存在することを確認できた!
もし、この配列の中に100が含まれるかを確認するために、
リストの先頭から「3 → 11 → … → 99 → 101」と調べていき、「100は無い」と判断する場合、
すなわち数字を1つずつ見て探した場合、探索回数は11回(\(O(n)\))になる。
一方の二分探索では、探索範囲が半分ずつ減っていくので、探索回数は\(O(logn)\)となる。。
コード例
# 値の探索
"""
ソート済みの数列 A に 値 k が含まれているなら true を、含まれていないなら no を返す
"""
n = int(input())
A = list(map(int, input().split()))
q = int(input())
# 二分探索をする関数を定義
def binary_search(A, n, k):
# 探索範囲
left = 0
right = n-1
# 探索範囲を狭めていく
while left <= right:
# 探索範囲の中央
mid = (left+right)//2
if A[mid] == k:
return True
elif A[mid] < k:
left = mid + 1
else:
right = mid - 1
return False
for i in range(q):
s = int(input())
print("Yes" if binary_search(A, n, s) else "No")注意点として、探索範囲の中央を
mid = (left+right)//2としているのは、Python特有である。C++などでは、
mid = (left+right)/2のように、「/」が割った値の整数部分表す。
3. 指定された数値 k 以上の値が現れる、最初の位置を取得する
問題
引用元:https://paiza.jp/works/mondai/binary_search/binary_search__basic_step1
\(n\) 人の生徒が受けた、\(10^9\) 点満点のテストの採点結果 \((A_1, A_2, … A_n)\) があります。あなたは合格点を自由に設定することができます。合格点が \(k\) 点のとき、\(k\) 点以上を取った生徒が合格で、\(k\) 点未満を取った生徒が不合格です。
\(q\) 個の整数 \(k_1, k_2, … k_q\) が与えられます。各 \(k_i\) について、合格点が \(k_i\) のときに合格する生徒の人数を答えてください。
なお、\(n, \ q\) の最大値はいずれも 200,000 です。
考え方
探索範囲を狭めていくのだが、配列において、「\(A_i \ge k\)を満たさない部分をそぎ落としていく」というイメージである。\(A[mid]< k\)であるとき、mid以下のインデックスの要素はすべてそぎ落とし(A[mid]もそぎ落とされる)、\(mid+1\)が\(left\)(残った部分の左端)になる訳である。
コード例
# lower_bound
n = int(input())
A = list(map(int, input().split()))
"""
A_i >= k を満たす最小の i を返す
A_i >= k を満たす i が存在しない場合は n を返す
"""
A.sort()
def binary_search_lower(A, n, k):
# 探索範囲
left = 0
right = n
# 探索範囲を狭めていく
while left < right:
# 探索範囲の中央
mid = (left + right)//2
if A[mid] < k:
# a[0] ~ a[mid] は k 未満なので調べる必要が無い
left = mid+1
else:
right = mid
return n - right
q = int(input())
for i in range(q):
k = int(input())
print(binary_search(A, n, k))4. 指定された数値 k より大きい値が現れる、最初の位置を取得する
問題
引用元:https://paiza.jp/works/mondai/binary_search/binary_search__basic_step2
\(n\) 人の生徒が受けた、\(10^9\) 点満点のテストの採点結果 \((A_1, A_2, … A_n)\) があります。あなたは合格点を自由に設定することができます。合格点が \(k\) 点のとき、\(k\) 点より大きい点数を取った生徒が合格で、\(k\) 点以下の点数を取った生徒が不合格です。
\(q\) 個の整数 \(k_1, k_2, … k_q\) が与えられます。各 \(k_i\) について、合格点が \(k_i\) のときに合格する生徒の数を答えてください。
考え方
全問では、\(A_i \ge k\)を満たす境界を見つければ、その場所が「条件を満たす最小値」であった。
ここでは、\(A_i > k\)を満たす境界を見つける必要がある。
「\(A_i > k\)を満たさない部分をそぎ落としていく」というイメージである。\(A[mid] \le k\)であるとき、mid以下のインデックスの要素はすべてそぎ落とし(A[mid]もそぎ落とされる)、\(mid+1\)が\(left\)(残った部分の左端)になる訳である。
コード例
# upper_bound
n = int(input())
A = list(map(int, input().split()))
"""
A_i > k を満たす最小の i を返す
A_i > k を満たす i が存在しない場合は n を返す
=> A_i <= k を満たす最大の i を返す
== (A_i > kを満たす最小のi)- 1
A_i > k を満たす i が存在しない場合は(全てk以下) n を返す
"""
A.sort()
def binary_search(A, n, k):
# 探索範囲
left = 0
right = n
# 探索範囲を狭めていく
while left < right:
# 探索範囲の中央
mid = (left + right)//2
if A[mid] <= k:
# a[0] ~ a[mid] は k 以下なので調べる必要が無い
left = mid+1
else:
right = mid
return n - right
q = int(input())
for i in range(q):
k = int(input())
print(binary_search(A, n, k))5. ある範囲に含まれている整数の個数
問題
引用元:https://paiza.jp/works/mondai/binary_search/binary_search__basic_boss
数列 \(A = (A_1, A_2, …, A_n)\) と、整数の組 \((l_1, r_1), \ (l_2, r_2), \ …, \ (l_q, r_q) \)が与えられます。各組 \((l_i, r_i) \)について、数列 \(A\) に含まれる値のうち \(l_i\) 以上 \(r_i\) 以下であるものの個数を求めてください。
考え方
この問題は、2つの要素に分解することができる。
まず、「昇順の数列 \(A\) に含まれる値のうち \(l_i\) 以上となる最初の値の位置を求めよ」
そして、「昇順の数列 \(A\) に含まれる値のうち \(l_i\) 以下となる最後の位置を求めよ」
「昇順の数列 \(A\) に含まれる値のうち \(l_i\) 以上となる最初の値の位置を求めよ」に関しては、
「指定された数値 k 以上の値が現れる、最初の位置を取得する」にて実装した関数をそのまま使えばよい。
「昇順の数列 \(A\) に含まれる値のうち \(l_i\) 以下となる最後の位置を求めよ」に関しては、ここまでで未だ解説をしていない。しかし、実はすでに実装自体は完成している。
というのも、
(「指定された数値 k より大きい値が現れる、最初の位置を取得する」で求めた位置) – 1
によって、「指定された数値 k 以下」となる最大の位置が判明するからである!
コード例
n = int(input())
A = list(map(int, input().split()))
A.sort()
"""
A_i >= k を満たす最小の i を返す
A_i >= k を満たす i が存在しない場合は n を返す
"""
A.sort()
def binary_search_low(A, n, k):
# 探索範囲
left = 0
right = n
# 探索範囲を狭めていく
while left < right:
# 探索範囲の中央
mid = (left + right)//2
if A[mid] < k:
# a[0] ~ a[mid] は k 未満なので調べる必要が無い
left = mid+1
else:
right = mid
return left
"""
A_i <= k を満たす最大の i を返す
== (A_i > kを満たす最小のi)- 1
A_i > k を満たす i が存在しない場合は(全てk以下) n を返す
"""
def binary_search_up(A, n, k):
# 探索範囲
left = 0
right = n
# 探索範囲を狭めていく
while left < right:
# 探索範囲の中央
mid = (left + right)//2
if A[mid] <= k:
# a[0] ~ a[mid] は k 以下なので調べる必要が無い
left = mid+1
else:
right = mid
return right
q = int(input())
for i in range(q):
low, up = map(int, input().split())
print(binary_search_up(A, n, up) - binary_search_low(A, n, low))6. まとめ
二分探索の基本問題の紹介および、Pythonでの実装例を紹介してきた。
他のアルゴリズムでも当てはまることだが、具体的な数字を使って考えてみるのが、理解への第一歩だと感じた。
やや応用的な内容に関しては、【二分探索(応用編)】を書く予定である。
競技プログラミングで二分探索を使いこなすには、多くの練習が必要なので、以下の記事のような問題を解いて実力を磨いていきたい。


コメント