【統計力学】固体比熱（１）古典論からデュロン=プティの法則を導出する

統計力学

2022.07.192022.07.27

本記事の目的

対象とする系の分配関数を求め、各物理量を求めるという統計力学の典型的な演習問題を解く実力を身に付ける。
固体比熱を、古典力学的なハミルトニアンから求め、その振る舞いを評価する。
デュロン=プティの法則とは何かを理解する。

固体は結晶構造（原子や分子が規則的に並んだ格子状の構造）を持つ。各原子（分子）は完全に止まっているわけではなく、微視的には常に振動している。そして、個体の温度が上がると各原子（分子）の振動は激しくなる。すなわち、固体の物理的性質は温度によって変化する。また、一般に固体の比熱は物質や温度によって異る。

ここで、固体を３次元的な格子状のモデルとして考え、各格子点を独立な調和振動子とみなすことで、３次元の結晶の比熱の振る舞いを調べる。

1. 系の分配関数を求める

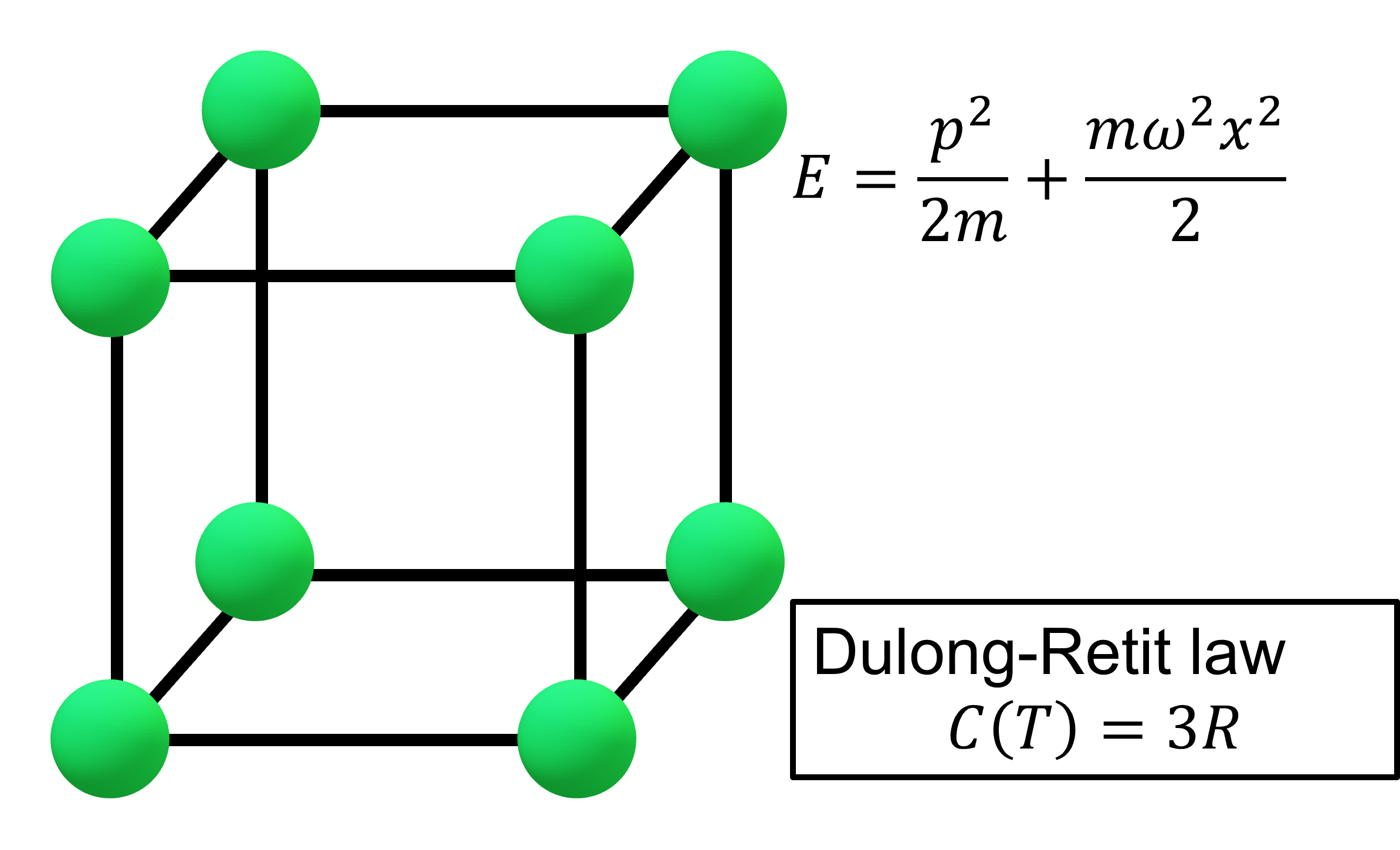
格子点上に存在するN個の粒子を、独立した（古典的力学的な）３次元調和振動子であるとする。この時、系のハミルトニアンは以下のように記述される。

$$H = \sum_{i=1}^{3N}\left(\frac{p_i^2}{2m}+\frac{m\omega^2x_i^2}{2}\right)$$

分配関数は次のように求めることができる。

\begin{align*}
Z &= \frac{1}{h^{3N}}\left( \prod_{i=1}^{N}\int d^3x_id^3p_i \right)e^{-\beta H}\\
&= \frac{1}{h^{3N}}\left( \prod_{i=1}^{N}\int d^3p_ie^{-\beta\frac{p_i^2}{2m}}\right)\left( \prod_{i=1}^{N}\int d^3x_ie^{-\beta\frac{m\omega^2x_i^2}{2}}\right)\\
&= \frac{1}{(2\pi\hbar)^{3N}}\left(\frac{2\pi m}{\beta}\right)^{\frac{3N}{2}}\left(\frac{2\pi}{\beta m\omega^2}\right)^{\frac{3N}{2}}\\
&= \left(\frac{kT}{\hbar\omega}\right)^{3N}
\end{align*}

ここで、理想気体数などの分配関とは異なり、格子点上に存在する各粒子を区別することができるので、N!で割る必要はないことに注意。

2. F, S, U そして比熱Cを求める

ヘルムホルツ自由エネルギーは

\begin{align*}
F &= -kTlnZ\\
&= -3NkTln\frac{kT}{\hbar\omega}
\end{align*}

エントロピーは

\begin{align*}
S &= -\frac{\partial F}{\partial T}\\
&= 3Nkln\frac{kT}{\hbar\omega} + 3NkT\cdot\frac{\partial}{\partial T}lnT\\
&= 3Nk\left(ln\frac{kT}{\hbar\omega}+1\right)
\end{align*}

固体結晶全体の格子振動による内部エネルギーの期待値は

\begin{align*}
U &= F + TS\\
&= 3NkT
\end{align*}

以上より、熱容量は

$$C = \frac{\partial U}{\partial T} = 3Nk = 3nR$$

ここで、nは結晶全体のモル数である。よって、この結晶モデルのモル比熱は3Rとなる。

3. デュロン・プティの法則の問題点

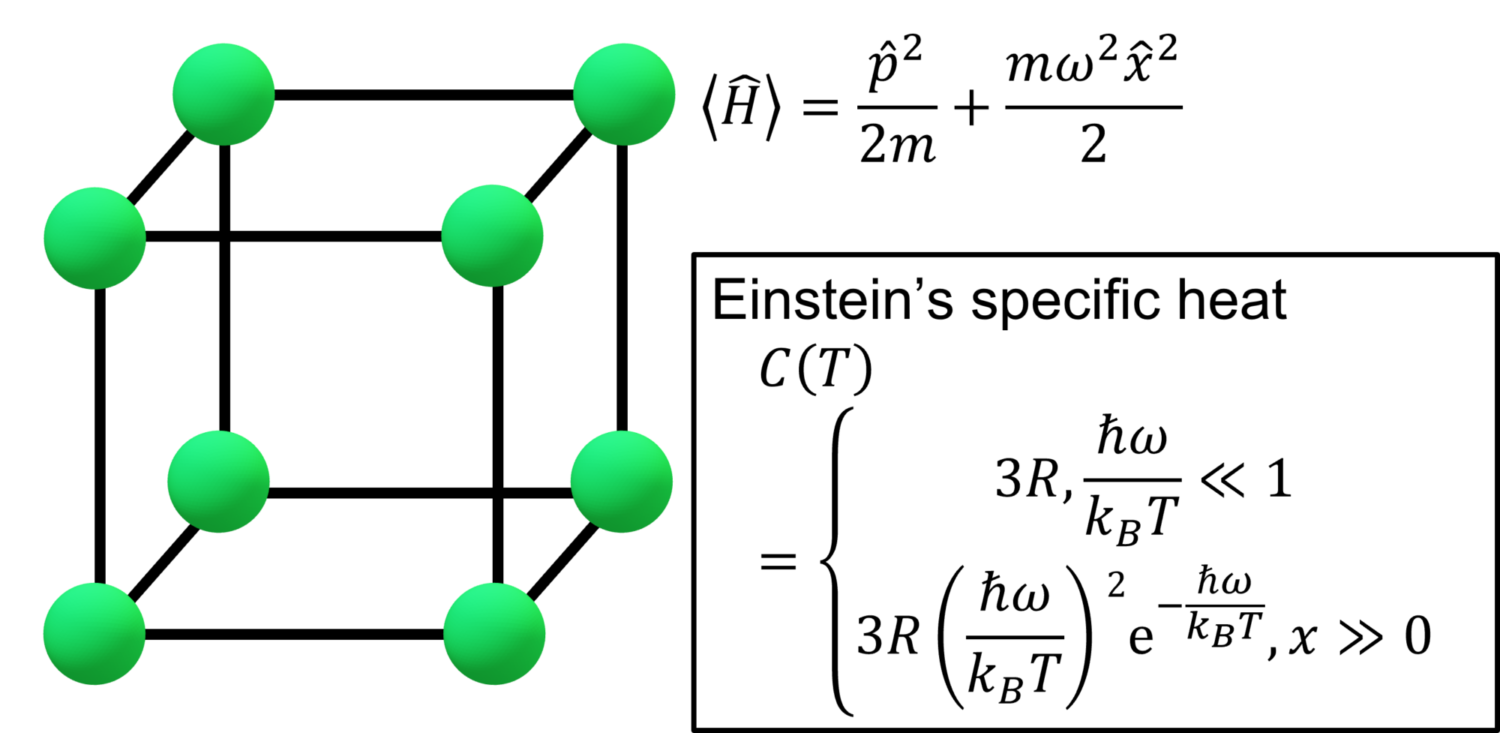
固体結晶のモル比熱は物質の種類や温度に依存せず3Rで一定であるという結果は、高温において実験結果と良く一致する。しかし、物質の比熱は温度の低下とともに単調に減少する。しかし、古典力学的なハミルトニアン（エネルギーの期待値）を用いたため、デュロン=プティの法則では、低温での比熱の振る舞いを正確に表現することができない。

そこで、次の記事では、アインシュタインモデルを導入し、量子力学的に求めたエネルギーの期待値を用いて、低温での比熱の振る舞いを調べる。