1. アインシュタインモデルとは
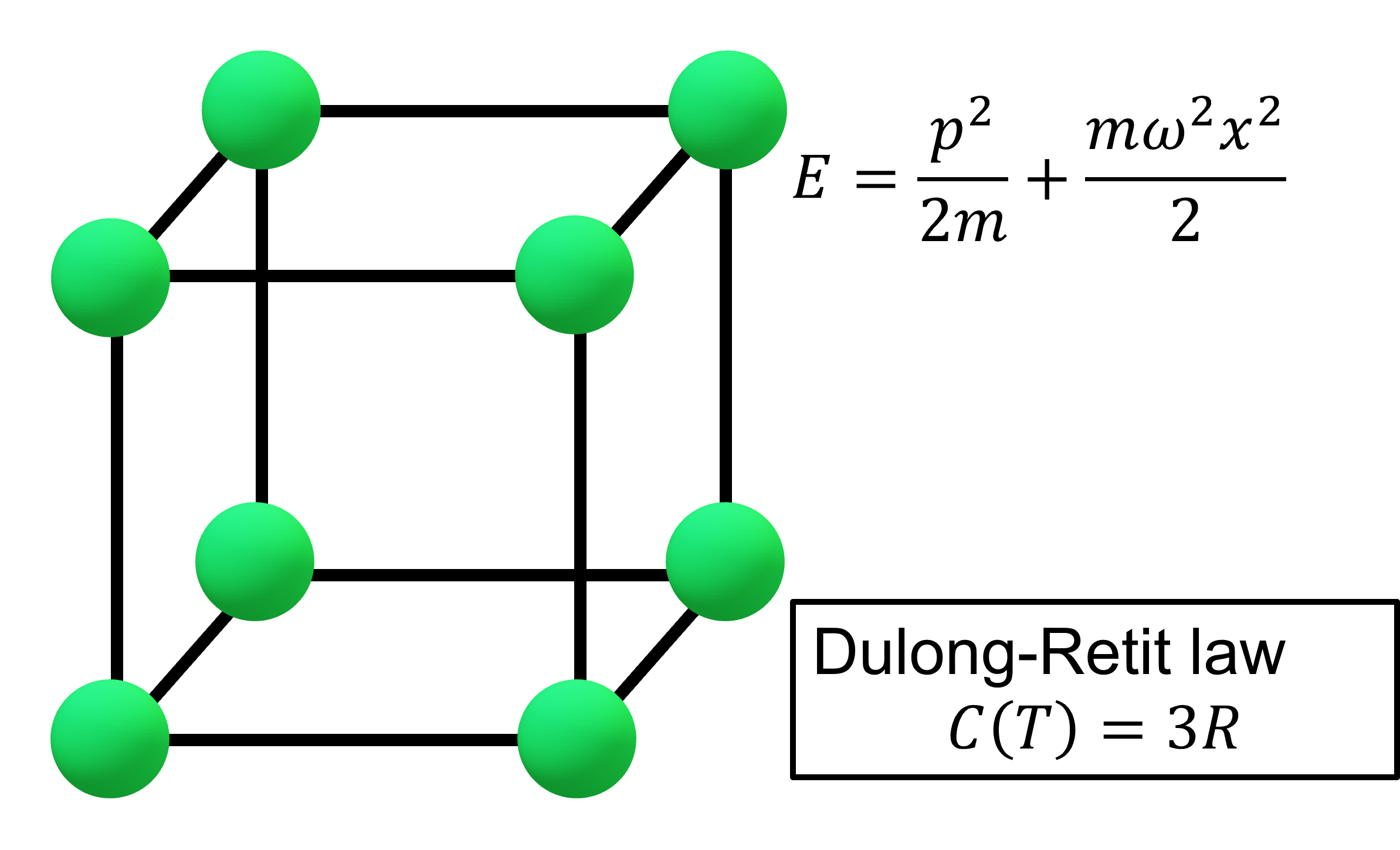
前回の記事↑では、デュロン=プティの法則を導出し、固体結晶の比熱は物質の種類や温度に依らず3Rで一定であるという結果が得られた。
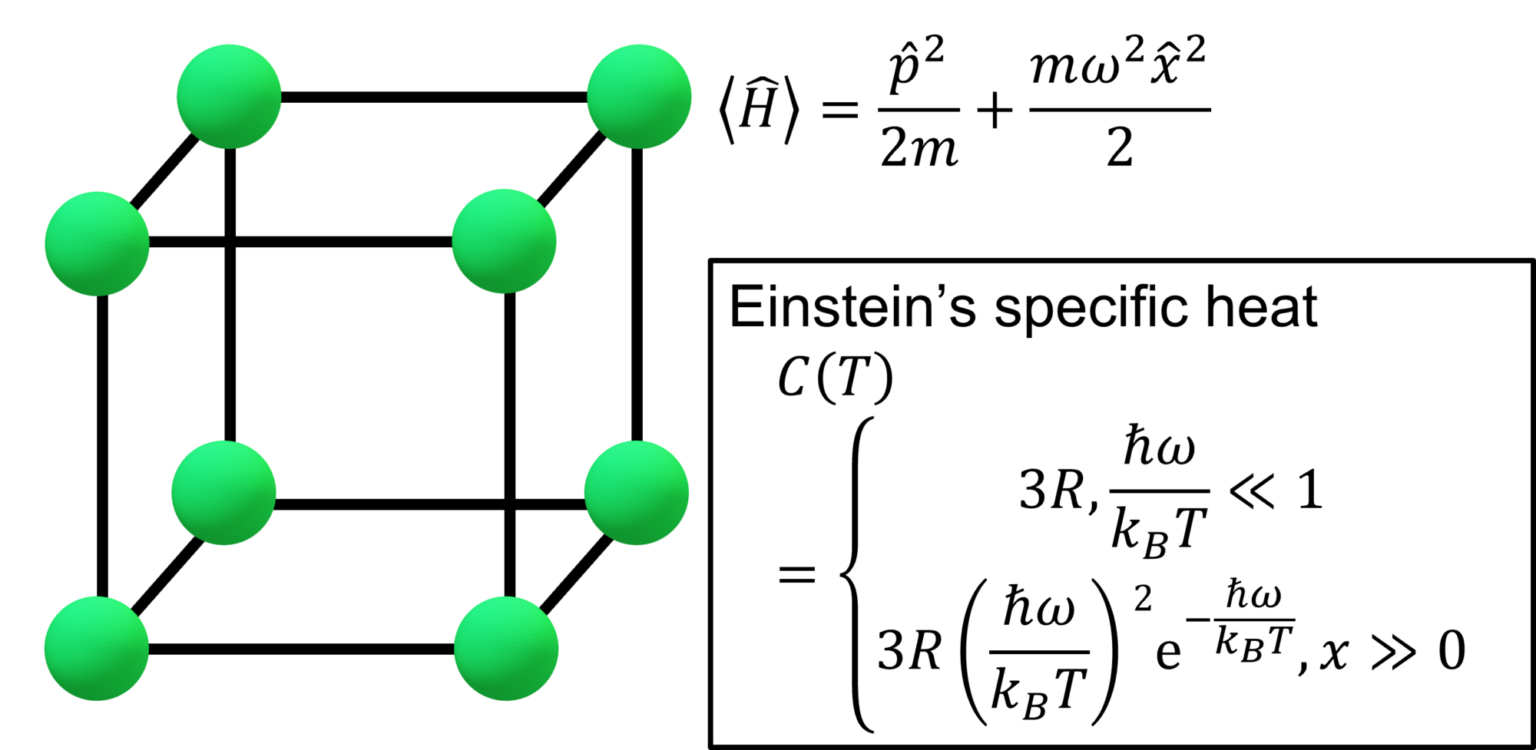
しかし、実験的には低温ほど固体の比熱は小さくなることが分かっている。この現象を数式表現するために、調和振動子としての各粒子を量子力学的に取り扱ったのが、アインシュタインモデルである。

2. 系の分配関数を求める
調和振動子のハミルトニアンは次のように書ける。
$$\hat{H} = \frac{1}{2m}(\hat{p}^2 + m^2\omega^2\hat{x}^2)$$
量子力学において、この系のエネルギー固有値は次のように書ける。
$$E_n = \left(n+\frac{1}{2}\right)\hbar\omega \ (n=0, 1, 2…)$$
よって、1つの1次元調和振動子の分配関数は次のように求まる。
\begin{align*}
Z_i &= \sum_{n_i=0}^{\infty}e^{-\beta\hbar\omega\left(n_i+\frac{1}{2}\right)}\\
&= e^{-\frac{\beta\hbar\omega}{2}}\sum_{n_i=0}^{\infty}\left(e^{-\beta\hbar\omega}\right)^{n_i}\\
&= e^{-\frac{\beta\hbar\omega}{2}}\cdot\frac{1}{1-e^{-\beta\hbar\omega}}\\
&= \left(2sinh\frac{\beta\hbar\omega}{2}\right)^{-1}
\end{align*}
3次元調和振動子に対応する量子系を考えると、N個の粒子が3つずつ自由度を持つ。よって、系全体の分配関数はそれらの総乗で表すことができる。
\begin{align*}
Z &= \prod_{i=1}^{3N}Z_i\\
&= \left(2sinh\frac{\beta\hbar\omega}{2}\right)^{-3N}
\end{align*}
3. 高温・低温における比熱Cを求める
内部エネルギーは
\begin{align*}
U &= -\frac{\partial}{\partial \beta}lnZ\\
&= 3N\frac{\partial}{\partial \beta}ln\left(2sinh\frac{\beta\hbar\omega}{2}\right)\\
&= 3Nfrac{\partial \left(\frac{\beta\hbar\omega}{2}\right)}{\partial \beta}\frac{\partial}{\partial \left(\frac{\beta\hbar\omega}{2}\right)}lnsinh\frac{\beta\hbar\omega}{2}\\
&= \frac{3N\hbar\omega}{2}\cdot\frac{cosh\frac{\beta\hbar\omega}{2}}{sinh\frac{\beta\hbar\omega}{2}}\\
&= \frac{3N\hbar\omega}{2}tanh^{-1}\frac{\beta\hbar\omega}{2}
\end{align*}
熱容量は
\begin{align*}
C &= \frac{\partial U}{\partial T}\\
&= \frac{\partial \beta}{\partial T}\frac{\partial U}{\partial \beta}\\
&= 3Nk\left(\frac{\hbar\omega}{kT}\right)^2\left(2sinh\frac{\hbar\omega}{2kT}\right)^{-2}
\end{align*}
上の計算にて\((tanh^{-1})’ = \frac{-1}{sinh^2}\)であることを用いた。
ここで、\(\frac{\hbar\omega}{kT}=x\)とおくと
\begin{align*}
C &= 3Nkx^2\cdot\frac{1}{(e^\frac{x}{2}-e^{-\frac{x}{2}})^2}\\
&= 3Nk\frac{x^2e^x}{(e^x-1)^2}\\
&= 3nR\frac{x^2e^x}{(e^x-1)^2}
\end{align*}
です。これを用いると、以下の低温・高温での振る舞いが分かる。
\(x << 1\)すなわち、十分高温のとき
\begin{align*}
C &\cong 3nRx^2\cdot\frac{1}{{(1+x) – (1-x)}^2}\\
&= 3nRx^2\frac{1}{x^2}\\
&= 3nR
\end{align*}
となる。これは、
で求めたデュロン・プティの法則と一致する。すなわち、理論上、固体(結晶)の比熱は高温において物質の種類や温度に一致しないことを示す。
\(x >> 1\)すなわち、十分低温のとき
\begin{align*}
C &\cong 3nRx^2e^{-x}\\
&= 3nR\left(\frac{\hbar\omega}{kT}\right)^2e^{\frac{\hbar\omega}{kT}}
\end{align*}
と近似できます。これは\(T \rightarrow 0\)で比熱が急激に小さくなることを示す。この、古典論だけでは導き出されなかった振る舞いこそが、量子効果の表れである。
統計力学Iでの表現を借りれば、低温になると調和振動子は「凍って」しまって、もはや熱を吸収しなくなる。
アインシュタインモデルの問題点
- 現実では、0K付近の低温における比熱の減少はそれほど急激ではなく、\(T^3\)に比例する。
- 結晶を構成するすべての粒子を独立な3次元調和振動子としたが、実際には各粒子は周囲の粒子の振動に影響を受けるはずである。
このような問題を解決するために、結晶を構成する粒子の集団的な振動を考慮したのが、デバイモデルであり、次の記事で詳しく見ていく。
【参考】
「統計力学I」田崎晴明 著


コメント