1. AtCoder ABC270 C – Simple path
木についての情報と頂点番号 X, Y が与えられるので、X から Y までの単純パス上の頂点(端点含む)を順に列挙せよという問題です。要するに、木構造において、XからYに向かう経路上の頂点を、通る順に出力すればよいです。
ここで、木上の任意の相異なる 2 頂点 a, b について、a から b への単純パスがただ一つ存在することが証明できることは前提としています。
問題文について詳しくはこちら:C – Simple path (atcoder.jp)
2. 幅優先探索と深さ優先探索の違い
幅優先探索と深さ優先探索の違いや、その用途については、AtCoder社長、高橋直大氏の一般向けの記事にて、図を用いて易しく解説されています。
よって、ここでは抜粋だけを記載し、軽い復習とします。
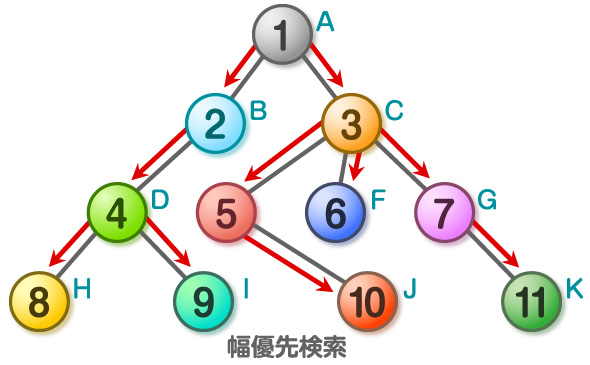
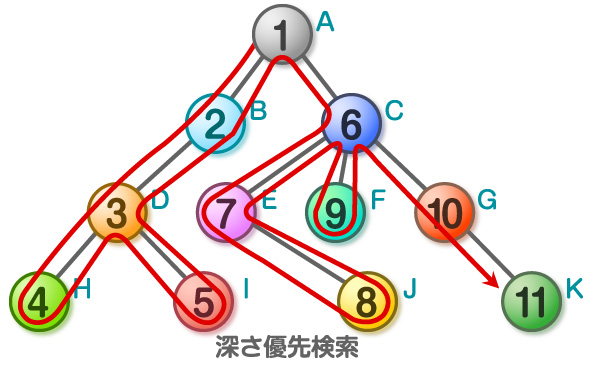
「幅優先探索」は、深さの浅い点(頂点Aからたどる辺の数が少ない点)から順番に、また、左側にある頂点から順番に、というルールの下で探索しています。一方、「深さ優先探索」では、とにかくなるべく左に深く進むというルールで探索しています。
引用元:ITmedia
引用元:https://image.itmedia.co.jp/enterprise/articles/1001/16/tnfig1.jpg
引用元:https://image.itmedia.co.jp/enterprise/articles/1001/16/tnfig2.jpg
3. 幅優先探索(BFS)による解法
幅優先探索の実装について詳しく記載しているので、是非ご覧ください。
ポイント
- g[i]に、頂点 i に隣接する頂点を格納することでグラフ(木)を表現する。
- 出発点Xを根とし、根に近いほうからdeque()の末尾に加えていく。
- dequeの先頭から処理していくことで、根に近いほうから先に処理される。
- upperリストに、各頂点の1つ前(1つ根に近い頂点)を記録していく。
- upperリストを使い、終点Yから出発点Xまでに通った点を復元する。
from collections import deque
N, X, Y = map(int, input().split())
# 木の情報を2次元リストに格納
g = [[] for _ in range(N)]
for _ in range(N - 1):
a, b = map(int, input().split())
a -= 1
b -= 1
g[a].append(b)
g[b].append(a)
q = deque()
q.append(X - 1)
upper = [-1] * N
# 頂点Aは根であることを, -2で表現する
upper[X - 1] = -2
def BFS():
while q:
# 先頭を取り出してnowとする
now = q.popleft()
# nowと隣接する要素nxtをすべて調べる
for nxt in g[now]:
# 未訪問なら"nxtの1つ前の要素"=nowを記録する
if upper[nxt] == -1:
upper[nxt] = now
q.append(nxt)
BFS()
ans = []
now = Y - 1
while upper[now] != -2:
ans.append(now)
now = upper[now]
ans.append(now)
# ansにはB=>Aとたどる経路を格納したので, 逆順に出力する
for i in ans[::-1]:
print(i + 1, end=" ")4. 深さ優先探索(DFS)による解法
DFSでの実装方法については、こちらのYoutube動画がわかりやすいです。Pythonでの実装例も紹介されていますので、おすすめです。
ポイント
- DFSはPyPyだとTLEに。PyPyだとTLEになる原因の考察の記事を見つけた。
- 再帰回数の上限はデフォルト値では足りないため、増やしておく設定が必要。
- g[i]に、頂点 i に隣接する頂点を格納することでグラフ(木)を表現する。
- 深さ優先探索を用いて、prevリストに、各頂点の1つ前(1つ根に近い頂点)を記録していく。
# 再帰回数の上限を増やしておく必要がある
from sys import setrecursionlimit
setrecursionlimit(10 ** 9)
# 木の情報を2次元リストに格納
N, X, Y = map(int, input().split())
X, Y = X - 1, Y - 1
g = [[] for _ in range(N)]
for _ in range(N - 1):
a, b = map(int, input().split())
a -= 1
b -= 1
g[a].append(b)
g[b].append(a)
# 地点 i の1つ前(の深さ)の地点
prev = [-1] * N
# DFS(今いる場所n, 前にいた場所p)
def DFS(n, p):
# 今いる場所から、行ける場所
for nv in g[n]:
# 行ける所が前にいた場所ならスルー
if nv == p:
continue
# 行ける場所に対する「前の場所」として現地点nを格納
prev[nv] = n
# 行ける場所=>今いる場所/今いる場所=>前にいた場所
DFS(nv, n)
# 前にいた場所は適当に-1としておく
DFS(Y, -1)
# 出力のための操作
now = X
path = [X + 1]
while prev[now] != -1:
# さかのぼっていく
now = prev[now]
path.append(now + 1)
print(*path) 5. 頂点間距離の求め方について
本記事と似た問題に、「2頂点間の距離の求める」というのがあります。
幅優先探索での実装方法を解説しているので、是非ご覧ください。
【参考】
https://paiza.jp/works/mondai/tree_primer/tree_primer__path




コメント
ABC270-Cを解いている中で、ルートを取り出すのはどうするのだろうと思いしらべていたところこちらにたどり着きました。丁寧なソースで理解できました。ありがとうございます。茶色になったばかりのものです。BFSでは先頭(X)から、DFSは逆(Y)から探索されているようですがなにか意味がありますでしょうか?Youtubeも見てみましたがスタート地点から探索をはじめているようでした。
返信が遅くなり申し訳ありません。ご質問ありがとうございます。
まず、確かにDFSの方は、逆(Y)から探索しています。
DFSで逆から探索しているのは、回答用に用意した配列を、そのままの順序で出力できるようになるためです(私の好みの問題ではあるのですが)。
参考までに、DFSのコードで、先頭(X)から探索する場合の例を書きます。
探索部分を以下のように変更して提出してもACになるはずです。おそらく、こちらの方が質問者様のイメージに合っていると思います。
# 前にいた場所は適当に-1としておく
DFS(X, -1)
# 出力のための操作
now = Y
path = [Y + 1]
while prev[now] != -1:
# さかのぼっていく
now = prev[now]
path.append(now + 1)
print(*path[::-1])