いくつかの記事を参考にしていますが、基本的に自力で解答することを目指しました。
今後に生かせるよう、汎用的で一般的な実装を行うことを心掛けました。
また、辞書的に利用できるよう、各問題に(個人的な)分類を記載しました。Ctrl + F のショートカットキーを使って、キーワードで問題を検索できます。
ABC042 C – こだわり者いろはちゃん(分類なし)
REになったコード。上から1桁ずつ確認していきますが、桁の繰り上がりに対応できない。
N, K = input().split()
D = list(map(int, input().split()))
Ns = list(N)
for i in range(len(N)):
Ns[i] = str(min(j for j in range(int(Ns[i]),10) if j not in D))
print(''.join(Ns))ACになったコード。O(10^5)程度なら、全探索できる。
N, K = map(int, input().split())
D = list(input().split())
#N以上の数をひとつずつ見ていく
for i in range(N, 100000):
cnt = 0
# Dの要素が含まれていないかの確認
for j in range(K):
if D[j] in str(i):
break
else:
cnt += 1
# Dの要素が1つも含まれていなかったら出力
if cnt == len(D):
print(i)
breakABC043 C – いっしょ(分類無し)
- N個の整数の最小値未満・最大値より大きい値は答えになりえないので、範囲を絞って線形探索。
- 距離の計算にはnumpyを使用。
import numpy as np
N = int(input())
A = list(map(int, input().split()))
ans = 10**10
arr = np.array(A)
for i in range(min(A),max(A)+1):
dist = np.sum((arr - i)**2)
if dist < ans:
ans = dist
print(ans)ABC044 C – 高橋君とカード(動的計画法・部分和数え上げ問題)
- 部分和数え上げ問題として解けるが、要素を用いて作る目的となる数が「総和」ではなく「平均」なので枚数の制限が入る。
- 通常の部分和問題を2次元だとすれば、3次元の部分和数え上げ問題である。
- dp[i][k][s] = i枚目までのカードでk枚選んで合計がsである組合せの数。
- 3次元のリスト(複数枚の表)を考えなければならないので、イメージしにくい。
NGだったコード。はじめ、2次元の部分和数え上げ問題で実装してしまった。「Aの倍数」となる総数は求まるが、「平均がA」であることを達成できない。
N, A = map(int, input().split())
X = list(map(int, input().split()))
# n * x の2次元配列を作成
dp = [[0]*2501 for _ in range(N)]
# 0列目はすべて1
for i in range(N):
dp[i][0] = 1
dp[0][X[0]] = 1
for i in range(1,N):
for j in range(2501):
if X[i] <= j:
dp[i][j] += dp[i - 1][j - X[i]] + dp[i -1][j]
else:
dp[i][j] = dp[i - 1][j]
print(sum(dp[N-1][j*A] for j in range(1, N+1)))ACとなったコード。
N, A = map(int, input().split())
X = list(map(int, input().split()))
# dp[i][k][s] = i枚目までのカードでk枚選んで合計がsである組合せ
# 合計の最大値は50*50
dp = [[[0]*2501 for j in range(N+1)] for i in range(N+1)]
dp[0][0][0] = 1
for i in range(N):
for k in range(N):
for s in range(2501):
# 組み合わせが1通り以上存在する場合
if dp[i][k][s]:
dp[i+1][k][s] += dp[i][k][s]
dp[i+1][k+1][s+X[i]] += dp[i][k][s]
r = 0
for k in range(1, N+1):
r += dp[N][k][k*A]
print(r)- dp[i][k][s]を中心に考える。
- カード i を選ばないとき、「k枚選ぶ」フィールドに値を追加。
dp[i+1][j+1][k] += dp[i][j][k] - カード i を選ぶとき、「k+1枚選ぶ」フィールドに値を追加。
dp[i+1][j+1][k+X[j]] += dp[i][j][k]
カード i を選んだ際に、「合計値kを実現できるか」と考えるのが通常のDP部分和問題であるが、「j枚選ぶ」という制約も加わっており、3次元のDP問題になっている。
【参考】
ARC 060 C – 高橋君とカード / Tak and Cards – srupのメモ帳 (hatenablog.com)
ABC045 C – たくさんの数式(ビット全探索)
- 長さがSの桁数に等しい2進数 i を用意すると、2進数で”+”の有無の全パターンを1or0で表現できる。i において1を示している場合、対応するSの桁の数字の前に「+」があると見なす。i において0を示している場合、対応するSの桁の数字の前に「+」が無いと見なす。
- 計算量は最大でもO(2^10)なのでビット全探索可能。
ビットシフトのやり方
i >> j # 右ビットシフト : 整数 i を受け取り、2進数に変換し、jだけ右にずらすdef main():
S = input()
tot = 0
# 全てのiを2進数で表すと、"+"の有無の全パターンを1or0で表現できる
for i in range(1<<(len(S)-1)):
# 現在の数字
tmp = 0
## どの桁が1になっているかをチェックするために2進数の各桁をループ
for j, c in enumerate(S):
# j:前から何桁目か, c:文字
# 現在の数字を10倍して、1の位に新たな数字を付けたす。
# 直前に"+"があるとき(or 左端)は、tmp = 0 としておく。
tmp = tmp * 10 + int(c)
## i >> jで確認したい桁を一番右までずらして1と論理積をとって「選択」している要素を確認
# 次の数の前に"+"がある場合、resultにtmpを加えて、次の数字は1の位として始まる
if i>>j & 1:
tot += tmp
tmp = 0
# 残った分を足す
tot += tmp
print(tot)
main() ただし、2進数 i の1の位⇔Sの1番目の桁
2進数 i の2の位⇔Sの2番目の桁
といったように、対応する桁が逆になっていることに注意。
直前に”+”がある時(or 左端)、現在の値を合計値に加えて、数字 j は1桁目になる。
直前に”+”が無いとき、現在の値の桁をずらして(10倍にして)新たな数字 j を末端に加える。
ABC046 C – AtCoDeerくんと選挙速報(長い数の割り算)
C – AtCoDeerくんと選挙速報 (atcoder.jp)
import math
N = int(input())
# i が付く方が現在の情報、つかない方が1手前の情報
for i in range(N):
Ti, Ai = map(int, input().split())
if i==0:
T, A = Ti, Ai
else:
if Ti >= T and Ai >= A:
T = Ti
A = Ai
else:
# 何倍にすればよいか
times = max(math.ceil(T/Ti), math.ceil(A/Ai))
Ti *= times
Ai *= times
T = Ti
A = Ai
print(Ti+Ai)これでサンプル3つを正解できたので、完璧だと思いきや、WAが出てしまった。原因は、Pythonでは割り算の値はfloat型であり、16桁程度しか保証されていないということ。
そこで思いついたのがこちら。
# 何倍にすればよいか
times = max(T//Ti + (T%Ti > 0), A//Ai + (A%Ai > 0))- 余りが存在するとき、1を加える。
- 余りが存在しないとき、0を加える。
とするためには、bool値を使えばよい。
【参考】
ARC-062 C-AtCoDeerくんと選挙速報: ceil関数の割り算に気をつけよう – Qiita
ABC047 C – 一次元リバーシ(計算量)
- 同じ色の石が並んだ部分は、その色の1つの石に置き換えて良い。BWBをすべてWにしたければ、左右にWを置けばよい。これは、BWWWBでも同じことである。
- BW, BWB, BWBW, … のどれに等価な列となっているかによって、答えが決まる。
S = input()
ans = 0
prev = S[0]
for s in S:
# 前の文字と同じか判定
# 1文字目は必ず一致する
if s != prev:
ans += 1
prev = s
print(ans)ABC048 C – Boxes and Candies(分類無し)
C – Boxes and Candies (atcoder.jp)
計算量はN*2程度なので、貪欲に解くことができる。
N, x = map(int, input().split())
a = list(map(int, input().split()))
ans = 0
for i in range(N-1):
# 隣り合う2セットを確認する
back, forth = a[i], a[i+1]
if back + forth <= x:
continue
# 過分
eat = back + forth - x
ans += eat
# なるべく右側を食べる
# 右側を食べれば済むとき
if forth >= eat:
a[i+1] -= eat
# 右側を食べるだけでは済まない(たりない)とき
else:
eat -= a[i+1] # 左側から食べるべき量
a[i+1] = 0
a[i] -= eat
print(ans)【参考】
AtCoder Beginner Contest 048 C – Boxes and Candies をPython3で解く | みゃおと鳴いたnet (miaoued.net)
ABC049 C – 白昼夢(分類無し)
Sの最後尾から単語を切り取っていけばいいという発想。
S = input()
words = ["dream"[::-1], "dreamer"[::-1], "erase"[::-1], "eraser"[::-1]]
S = S[::-1]
while len(S) >= 5:
if S[:7] == words[1]:
S = S[7:]
elif S[:6] == words[3]:
S = S[6:]
elif S[:5] == words[0]:
S = S[5:]
elif S[:5] == words[2]:
S = S[5:]
else:
break
print("YES" if len(S)==0 else "NO")index out of rangeに引っかかるのではないかと心配したのだが、
"abcde"[:6]
>> 'abcde'のように正常に動作することを確認した。
ABC050 C – Lining Up(偶奇の利用)
対称の位置に並んでいる人は、同じ値を持つはずである。それを利用したい。
- 「矛盾するか否か」を確認するcheck関数を作成する。
- check()=Falseなら0, check()=1なら場合の数を数える。
- 場合の数は、探索せずとも、配列の長さの偶奇で決まる。
- count()関数はO(N)の計算量がかかってしまい、最悪全体でO(N^2)なので何か工夫をしたい。
N = int(input())
a = list(map(int, input().split()))
mod=10**9+7
a.sort()
def check(a):
length = len(a)
if length%2==0:
for i in range(length//2):
if a[2*i]==a[2*i+1]==2*i+1:
continue
else:
return False
return True
else:
for i in range(length//2+1):
if i == 0:
if a[0]==0:
continue
else:
return False
else:
if a[2*i-1]==a[2*i]==2*i:
continue
else:
return False
return True
def cnt(a):
length=len(a)
if check(a):
print(2**(length//2)%mod)
else:
print(0)
cnt(a)これで計算時間が2300ms→90msに短縮した!このチャレンジを初めてから、300点問題を初めて自力だけで解くことができた。
ABC051 C – Back and Forth(分類無し)
C – Back and Forth (atcoder.jp)
- 1周目は点t-s間を最短距離で1周する。
- 2周目は点t-s間を、1周目よりも1周り大きく1周する。
sx, sy, tx, ty = map(int, input().split())
forth1 = "U"*(ty-sy) + "R"*(tx-sx)
back1 = "D"*(ty-sy) + "L"*(tx-sx)
forth2 = "L" + "U"*(ty-sy+1) + "R"*(tx-sx+1) + "D"
back2 = "R" + "D"*(ty-sy+1) + "L"*(tx-sx+1) + "U"
print(forth1+back1+forth2+back2)ABC052 C – Factors of Factorial(素因数分解)
AtCoder Beginner Contest 052 – AtCoder
ある数Nを次のように素因数分解できるとき、Nの約数の総数は第2式で表せる。
\begin{align*}
& N = x_1^{q_1}x_2^{q_2}\cdots x_n^{q_n}\\
& \displaystyle \prod_{i=1}^n (q_i + 1) = (q_1 + 1) \times (q_2 + 1) \times \cdots \times (q_n + 1)
\end{align*}
- 素数を列挙する関数を実装し、N!の素因数分解を行う。
- 素数の列挙にはCounter()を使用する。
※エラトステネスの篩(ふるい)を使うという方法もある。 - N!の素因数分解が完了すれば、公式を用いて約数の総数が求まる。
Counterは定義していないkeyを最初から使えるのが便利である。
dictionary = {}
dictionary[0]
>> KeyError: 0from collections import Counter
counter = Counter()
counter[0]
>> 0そして、Counter()オブジェクト同士の演算までできる。便利すぎる。
cnt_0 = Counter()
cnt_0[0], cnt_0[1] = 3, 4
cnt_1 = Counter()
cnt_1[0], cnt_1[1], cnt_1[2] = 5, 7, 10
print(cnt_0 + cnt_1)
>> Counter({1: 11, 2: 10, 0: 8})以下、提出コード例。
import math
from collections import Counter
# 素数であるか否かを判定する関数
def is_prime(n):
if n <= 1:
return False
for _ in range(2, int(math.sqrt(n)) +1):
if n % _ == 0:
return False
return True
# 素因数分解を行う関数
def prime_factorization(n):
# Counterクラスを呼び出してオブジェクト生成
counter = Counter()
# 素数で割り切れるかの判定
for p in primes:
# p**2 > n となるとき,pはnの(素)因数ではあり得ない
if p > math.sqrt(n):
break
# 1回割り切れるごとに+1カウントしていく
while n%p == 0:
counter[p] += 1
n //= p
# n が1より大きい数字として残っていれば、素数
if n != 1:
counter[n] += 1
return counter実装した関数を用いて問題を解く。
N = int(input())
mod = 10**9 + 7
# N以下の素数を列挙する
primes = [n for n in range(N+1) if is_prime(n)]
# N!=1*2*...*Nを構成する1~Nのそれぞれを素因数分解し
# 各素因数が何回かかっているのか調べる
primes_counter = Counter()
for i in range(1, N+1):
primes_counter += prime_factorization(i)
ans = 1
for value in primes_counter.values():
ans *= (value + 1)
print(ans%mod)【参考】
こちらのサイトには何度もお世話になっている。
AtCoder Regular Contest 067 C – Factors of Factorial をPython3で解く | みゃおと鳴いたnet (miaoued.net)
ABC053 C – X: Yet Another Die Game(計算量)
C – X: Yet Another Die Game (atcoder.jp)
- 6, 5, 6, 5… と繰り返し目を出していけば、最短で目的の合計値以上を達成することができる。
- 線形探索では最大で10^15回のループを回さなければならず、非現実的。
- 基本的に5+6=11をセットで考えて、割り切れない部分の扱を処理すればよい。
n=int(input())
ans = 0
ans += n//11*2
if n%11:
if n%11 -6 <= 0:
ans += 1
else:
ans += 2
print(ans)ABC054 C – One-stroke Path(無向グラフ)
C – One-stroke Path (atcoder.jp)
- 隣接行列を生成し、2つの頂点のペアが辺で結ばれているかを表現する。
- itertools.permutations()によって1~Nからできる全順列を生成する。
- それぞれの順列に対して、ノード1から始まっているかをチェックしたうえで、Trueなら、順列の次の要素と辺で結ばれているか探索していく。
import itertools
routes = itertools.permutations(range(1, 4)) # 1~3の数字から作ることのできる全順列を生成
print(*routes, sep="\n")
>>
(1, 2, 3)
(1, 3, 2)
(2, 1, 3)
(2, 3, 1)
(3, 1, 2)
(3, 2, 1)import itertools
N, M = map(int, input().split())
#木の入力の受け取り(隣接行列)
tree_matrix = [[0]*N for _ in range(N)]
for i in range(M):
a, b = map(int, input().split())
tree_matrix[a-1][b-1] = 1
tree_matrix[b-1][a-1] = 1
routes = sorted(itertools.permutations(range(1, N+1)))
tot = 0
# それぞれのルートが条件を満たすかどうか判定する
for r in routes:
r = list(r)
if r[0] == 1:
check = [False]*(N-1)
else:
break
for i in range(N-1):
curr_ = r[i] # 今いるノード
next_ = r[i+1] # 次のノード
if tree_matrix[curr_-1][next_-1]:
check[i] = True
else:
break
if all(check):
tot += 1
print(tot)【参考】
itertools — 効率的なループ実行のためのイテレータ生成関数
ABC055 C – Scc Puzzle(計算量)
- 最初にN個のSを消費する。
- cが足りない場合の処理を実装できれば簡単。
N, M = map(int, input().split())
# SはN個だけとしたとき、何個ペアを作れるか
# ccはM個のcからM//2個まで作れる
tot = min(N, M//2)
# 残るcの数
M -= 2*tot
if M >= 4:
tot += M//4
print(tot)ABC056 C – Go Home(計算量)
- その場にとどまるという選択肢の存在に注目する。
- 時刻iまでの最大移動距離がX以上でありさえすれば、座標Xにたどり着ける。
- 最悪時刻 X-iまで移動を一切せずに、1度Xだけジャンプすればいいので、ループの末端はXとしておく。
X = int(input())
for i in range(1, X+1):
tot = i * (i + 1) //2
if tot >= X:
print(i)
breakABC057 C – Digits in Multiplication(計算量)
AtCoder Beginner Contest 057 – AtCoder
- A < Bと考えれば、Aの探索範囲は1 ≦ A ≦ sqrt(N) で十分である。
import math
N = int(input())
min_F = 11
# Aについてのループ
for A in range(1, int(math.sqrt(N))+1):
if N%A==0:
B = str(N//A)
min_F = min(min_F, len(B))
print(min_F)ABC058 C – 怪文書(カウント)
- 辞書にはアルファベット順で格納しているので、最後の出力もスムーズに完了する。
n = int(input())
dic = {}
# カウンターを定義
for alf in "abcdefghijklmnopqrstuvwxyz":
dic[alf] = 50
for i in range(n):
s = input()
for alf in "abcdefghijklmnopqrstuvwxyz":
dic[alf] = min(dic[alf], s.count(alf))
string = ""
for key, value in dic.items():
string += key*value
print(string)ABC059 C – Sequence(偶奇の利用)
- 正負…または負正…のどちらかのパターンになる。
N = int(input())
A = list(map(int, input().split()))
def f(p):
tot = 0
cnt = 0
for i, a in enumerate(A):
tot += a
if i%2 == p and tot <= 0:
cnt += 1 - tot
tot = 1
elif i%2 != p and tot >= 0:
cnt += tot + 1
tot = -1
else:
continue
return cnt
print(min(f(0), f(1)))ABC060 C – Sentou(区間の扱い)
- 流水が継続しているのか、途切れるのかを判定すればよい。
N, T = map(int, input().split())
ts = list(map(int, input().split()))
left = 0
tot = 0
for i, t in enumerate(ts):
if i == 0:
right = T
continue
if t <= right:
right = t + T
else:
tot += right - left
left = t
right = t + T
tot += right - left
print(tot)ABC061 C – Big Array(累積和・ソート)
- Counter()または辞書型で各数字の個数を管理。
- キーで辞書型をソートする。
- itertools.accumulate()を用いて、ソートした辞書型のvalueを累積和にする。
- bisect_leftを用いて、K番目の数字が累積和のどこに挿入できるかを見つける。
import itertools
import bisect
N, K = map(int, input().split())
dic = {}
for i in range(N):
a, b = map(int, input().split())
if a not in dic.keys():
dic[a] = b
else:
dic[a] += b
dic_sorted = sorted(dic.items())
def tups_to_lists(tup_list):
return [list(tup) for tup in zip(*tup_list)]
# 何個蓄積しているか
acc = list(itertools.accumulate(tups_to_lists(dic_sorted)[1]))
# K番目はどこにいるか
idx = bisect.bisect_left(acc, K)
print(tups_to_lists(dic_sorted)[0][idx])【参考】
辞書型のソート(keyでソート・valueでソートなど):
https://techacademy.jp/magazine/19309
ABC062 C – Chocolate Bar(図形)
C – Chocolate Bar (atcoder.jp)
- 同じような計算が多いので、関数化するのが吉。
- 3つの行(列)に分割するパターンの実装には、少し工夫が必要。
H, W = map(int, input().split())
def tsplit(h, w):
diff = 10**10
for a in range(1, h):
Sa = a*w
Sb = (h-a)*(w//2)
Sc = (h-a)*(w - w//2)
diff = min(diff, max(Sa, Sb, Sc) - min(Sa, Sb, Sc))
return diff
def isplit(h, w):
if h%3 == 0:
return 0
else:
return w
print(min(tsplit(H,W), tsplit(W,H), isplit(H, W), isplit(W, H)))ABC063 C – Bugged(分類無し)
- 合計値 tot を求めておく。
- totの1の位が0でなければ、そのまま tot を出力。
- tot の1の位が0ならば、入力値のうち、1の位が0でない数の最小値を totから引けばよい。(10の倍数はいくら足しても1の位には影響しない)
N = int(input())
ss = []
no_zero = []
for i in range(N):
s = input()
ss.append(int(s))
if s[-1]!="0":
no_zero.append(int(s))
tot = sum(ss)
if str(tot)[-1]=="0":
if len(no_zero) != 0:
print(tot - min(no_zero))
else:
print(0)
else:
print(tot)ABC064 C – Colorful Leaderboard(分類無し)
C – Colorful Leaderboard (atcoder.jp)
- 3200以上のスコアしかいない場合、最小値は0にはならないことに注意。
# 064
N = int(input())
A = list(map(int, input().split()))
# カウンターを生成
dic = {}
for i in range(9):
dic[i] = 0
for a in A:
if 1 <= a <= 399:
dic[0] += 1
elif 400 <= a <= 799:
dic[1] += 1
elif 800 <= a <= 1199:
dic[2] += 1
elif 1200 <= a <= 1599:
dic[3] += 1
elif 1600 <= a <= 1999:
dic[4] += 1
elif 2000 <= a <= 2399:
dic[5] += 1
elif 2400 <= a <= 2799:
dic[6] += 1
elif 2800 <= a <= 3199:
dic[7] += 1
else:
dic[8] += 1
base = 0
for key, value in dic.items():
if key < 8 and value:
base += 1
p_alpha = dic[8]
print(max(1, base), base + p_alpha)ABC065 C – Reconciled?(分類無し)
AtCoder Beginner Contest 065 – AtCoder
- 犬と猿の数で場合分けする。
- 階乗はmath.factorial()で計算してくれる。
import math
N, M = map(int, input().split())
mod = 10**9 + 7
if N == M:
print(2*math.factorial(N)*math.factorial(M)%mod)
elif N == M + 1 or N == M -1:
print(math.factorial(N)*math.factorial(M)%mod)
else:
print(0)ABC066 C – pushpush(偶奇の利用・deque)
TLE:2111ms insertが計算量的に良くないと思われる。
n = int(input())
A = list(map(int, input().split()))
B = []
for i, a in enumerate(A):
# 奇数番目
if i%2 == 0:
B.append(a)
else:
B.insert(0, a)
# 偶数個 or 奇数個で変わる
if n%2 == 0:
print(*B)
else:
print(*B[::-1])AC:196ms
- データの追加をO(1)で済ませるには、両端からデータを追加・削除できる配列
deque(double-ended queue)を使用すればよい。 - 右から追加するデータと左から追加するデータを分ける方法もあるが、スライスの逆順出力を使えば、その必要はない。
from collections import deque
n = int(input())
A = list(map(int, input().split()))
B = deque() # double-ended queue
for i, a in enumerate(A):
# 奇数番目
if i%2 == 0:
B.append(a)
else:
B.appendleft((a))
# 偶数個 or 奇数個で変わる
if n%2 == 0:
print(*B)
else:
print(*list(B)[::-1])ABC067 C – Splitting Pile(累積和)
C – Splitting Pile (atcoder.jp)
- 累積和を使って、先にカードを引く人の、引いた枚数ごとの総和を求める。
import itertools
N = int(input())
A = list(map(int, input().split()))
tot = sum(A)
acc = list(itertools.accumulate(A))
for i in range(N-1):
diff = abs(tot - 2*acc[i])
if i == 0:
mi = diff
else:
mi = min(mi, diff)
print(mi)※bisectをimportしていたが、結局使わなかった。すると、全ケースでREが発生した。使わないライブラリのインポートはREの原因となる。
ABC068 C – Cat Snuke and a Voyage(無向グラフ)
C – Cat Snuke and a Voyage (atcoder.jp)
- 隣接行列を使う必要があるか?と思ったが、2つの集合を用意すれば十分だった。
one_to = set()
to_N = set()
N, M = map(int, input().split())
for _ in range(M):
a, b = map(int, input().split())
if a==1:
one_to.add(b)
elif b ==1:
one_to.add(a)
if a==N:
to_N.add(b)
elif b==N:
to_N.add(a)
print("POSSIBLE" if len(one_to & to_N) else "IMPOSSIBLE")【参考】
setの使い方:
https://note.nkmk.me/python-set/
ABC069 C – 4-adjacent(分類無し)
- 長さLの配列がある時、4の倍数がL//2個あれば目標達成できる。
- 2の倍数はペアで条件を満たすが、単体では意味がない。
- よって、2の倍数(2*奇数)となる数列Aと、それ以外の数列Bに分ける。
- 数列Bの中で、4の倍数がそうでない数以上の個数存在すれば、目標達成。
N = int(input())
A = list(map(int, input().split()))
two_num = 0
four_num = 0
for a in A:
if a%4 == 0:
four_num += 1
elif a%2 == 0:
two_num += 1
print("Yes" if (two_num > 1 and 2*four_num >= N - two_num) or (four_num >= N//2) else "No")ABC070 C – Multiple Clocks(最小公倍数)
C – Multiple Clocks (atcoder.jp)
- 最小公倍数を求める問題である。最小公倍数を求める関数の実装方法は以下の通り。
- 2つの数値を引数とする関数を、functools.reduceで3つ以上の数値に対応させることができる。
# 最小公倍数を求める関数
def lcm(a, b):
y = a * b // math.gcd(a, b)
return y
# array : 配列
def lcm_arr(array):
return functools.reduce(lcm, array)
lcm_arr([10, 12, 15, 30])
>> 60import math
import functools
def lcm(a, b):
y = a * b // math.gcd(a, b)
return y
# array : 配列
def lcm_arr(array):
return functools.reduce(lcm, array)
N = int(input())
arr = []
for _ in range(N):
arr.append(int(input()))
print(lcm_arr(arr))【参考】
最小公倍数 (LCM) の実装 (atelierkobato.com)
functools.reduce():演算を連続的に作用させて1つの値に集約させる (atelierkobato.com)
ABC071 C – Make a Rectangle(図形)
C – Make a Rectangle (atcoder.jp)
- 同じ長さの棒が何本あるかをカウントしておく。
- なるべく長い棒でペアを作る。
- ABC061でも使った辞書型のソートを行う。
N = int(input())
A = list(map(int, input().split()))
dic = {}
for a in A:
if a not in dic.keys():
dic[a] = 1
else:
dic[a] += 1
# 降順のソート
dic_sorted = sorted(dic.items(), reverse=True)
def tups_to_lists(tup_list):
return [list(tup) for tup in zip(*tup_list)]
counter = tups_to_lists(dic_sorted)
pairs = []
# i: Aに含まれるユニークな値, n: 対応するiの個数
for i, n in zip(counter[0], counter[1]):
if n // 2 == 1:
pairs.append(i)
elif n //2 >= 2:
pairs.append(i)
pairs.append(i)
if len(pairs) >= 2:
print(pairs[0]*pairs[1])
break
if len(pairs)==0:
print(0)ABC072 C – Together(カウント)
- 各aiに対して、考えられる値は-1~10^5+1であるから、それらをキーとした辞書型を生成。
- 各aiについて、3パターンの値を生成し、辞書にカウントする。
- valueの最大値を出力。
【イメージ】
0 ← X = 0
1 1 ← X = 1
2 2 2 ← X = 2
3 3 ← X = 3
4 ← X = 4
N = int(input())
A = list(map(int, input().split()))
dic = {}
for i in range(-1, 10**5+2):
dic[i] = 0
for a in A:
dic[a-1] += 1
dic[a] += 1
dic[a+1] += 1
print(max(list(dic.values())))ABC073 C – Write and Erase(偶奇の利用)
C – Write and Erase (atcoder.jp)
- 偶数回出現する値は最終的に消え、奇数回出現する値は残る。
- 出現回数をカウントし、最後に各値の偶奇を判定。
- aiの考えられる値10^9個すべてをキーとした辞書を生成してしまうと計算時間がかかるので、出現した数の分だけ、要素を生成する。
N = int(input())
dic = {}
for i in range(N):
a = int(input())
if a not in dic.keys():
dic[a] = 1
else:
dic[a] += 1
result = 0
for v in dic.values():
result += v%2
print(result)ABC074 C – Sugar Water(濃度の最大化)
- 物質の総量(砂糖と水の質量の和)x + y <= F
- 砂糖の総量 y < E * x // 100
- 濃度 c = 100 * y / (x + y) が最大値
という3つの条件を満たす値を更新していく。
# 074
A, B, C, D, E, F = map(int, input().split())
water = []
suger = []
for i in range(31):
for j in range(31):
x = 100*A*i + 100*B*j
if 100*A <= x <= F:
water.append(x)
for i in range(F):
for j in range(F):
y = C*i + D*j
if y <= F:
suger.append(y)
sw = A*100
s = 0
c_max = 0
for x in water:
for y in suger:
c = 100 * y / (x + y)
if x + y <= F and y <= E * x // 100 and c_max < c:
sw = x + y
s = y
c_max = c
print(sw, s)ABC075 C – Bridge(無向グラフ・深さ優先探索)
N, M = map(int, input().split())
# 隣接行列を生成
matrix = [[0] * N for _ in range(N)]
#visited = [0] * N
A = []
B = []
# 深さ優先探索ですべての頂点が連結されているか判定
def dfs(v):
# 頂点 v を訪問済みにする
visited[v] = 1
for v2 in range(N):
# 頂点 v と頂点 v2 との結合が無い場合
if matrix[v][v2] == 0:
continue
# v2 は訪問済みの場合
if visited[v2] == 1:
continue
dfs(v2)
# 隣接行列に辺の登録
for i in range(M):
a, b = map(int, input().split())
A.append(a-1)
B.append(b-1)
matrix[a-1][b-1] = 1
matrix[b-1][a-1] = 1
ans = 0
for i in range(M):
# 辺を消す
matrix[A[i]][B[i]] = matrix[B[i]][A[i]] = 0
# 訪問履歴を初期化
visited = [0] * N
# 頂点visited[0]を始点とし、各頂点を可能な限り訪問する
dfs(0)
bridge = 0
for j in range(N):
# (辺 i を消したことで)訪問できなかった頂点があれば i は橋である
if visited[j] == 0:
bridge = 1
break
# 辺 i が橋なら +1
if bridge:
ans += 1
# 辺を元に戻す
matrix[A[i]][B[i]] = matrix[B[i]][A[i]] = 1
print(ans)【参考】
公式解説(C++での実装方法)を参考にした。
ABC076 C – Dubious Document 2(分類無し)
C – Dubious Document 2 (atcoder.jp)
Sd = input()
T = input()
candidate = []
for i in range(len(Sd) - len(T)+1):
Sdd = list(Sd)
flag = False
for j in range(len(T)):
if Sd[i+j] == T[j] or Sd[i+j] == "?":
Sdd[i+j] = T[j]
else:
break
if j == len(T) - 1:
flag = True
if flag == False:
continue
Sdd = ''.join(Sdd)
Sdd = Sdd.replace("?","a")
candidate.append(Sdd)
print(sorted(candidate)[0] if len(candidate)>0 else "UNRESTORABLE")ABC077 C – Snuke Festival (二分探索)
C – Snuke Festival (atcoder.jp)
- A, B, C各数列をソートすれば、ある数列の各要素に対して、他の数列において、ペアとなりうるか否かの境界をbisectで絞ることができる。
- Aの要素a対して、Bにおける有効な値の範囲を求める→Bの有効な各要素bに対して、Cにおける境界を求める、と2重ループを組むことで解けるが、これではTLEになってしまう。
- しかし、Bの要素bを基準に、「Aにおいてbより小さな値の数×Cにおいてbより大きな値」の数を求めれば、O(N*2*logN)の計算量に収まる。
import bisect
N = int(input())
A = sorted(list(map(int, input().split())))
B = sorted(list(map(int, input().split())))
C = sorted(list(map(int, input().split())))
ans = 0
for b in B:
lower_num = bisect.bisect_left(A, b)
upper_num = N - bisect.bisect_right(C, b)
ans += lower_num * upper_num
print(ans)ABC078 C – HSI(無限等比級数)
期待値の定義
\begin{alingn*}
& X = \sum_i x_ip_i \\
X : 期待値\\
x_i : 事象 i が起きたときに得られる値\\
p_i : 事象 i が起きる確率
\end{align*}
これを踏まえて、今回の問題における期待値を考えてみる。愚直に考えれば、
$$X = t\cdot p + 2t\cdot p^2 + 3t\cdot p^3 + …$$
(\(t\) は1回の試行にかかる時間)。1項ずつ足していけば解を得られるが、そのループは無限に続くため、間違いなくTLEを引き起こしてしまう。そこで、期待値をシンプルな表現に変換する必要がある。
ここで、\(n\) 回目の試行で操作が終了する確率\(p_n\)を考える。\(n-1\) 回失敗した後、1回だけ成功する必要があるので、各試行において、成功する確率は \(p\), 失敗する確率は \(q = 1-p\) 。よって
$$p_n = pq^{n-1} $$
1回の試行にかかる時間を \(t\) とすると、求めるべき期待値を次のように表せる。
\begin{align*}
X &= \sum_{n=1}^{\infty} nt\cdot p_n\\
&= \sum_{n=1}^{\infty} nt\cdot pq^{n-1}
\end{align*}
あとは、これを無限等比級数の公式を用いて上手く整理することにより、
$$X = \frac{t}{p} = 2^Mt$$
が得られる。
n, m = map(int, input().split())
print((2 ** m) * (1900 * m + 100 * (n - m)))この問題は、アルゴリズムと言うより、もはや数学の問題だった。
【参考】
無限級数の部分の式変形に関しては、以下のサイトが分かりやすい。
[AtCoder] ABC 078 C – HSI | ヤマカサの競技プログラミング (yamakasa.net)
ABC079 C – Train Ticket(符号の全探索)
- 全探索しても8ループにしかならないので、3重ループを回す。
- 難易度は高くないが、最も内側のループでans==7を満たしたとき、外側の2つのループからも抜け出す必要がある。
S = input()
pm = ["-", "+"]
for i in range(2):
if i:
ii = 1
else:
ii = -1
for j in range(2):
if j:
jj = 1
else:
jj = -1
for k in range(2):
if k:
kk = 1
else:
kk = -1
ans = int(S[0]) + ii*int(S[1]) + jj*int(S[2]) + kk*int(S[3])
if ans == 7:
print(S[0]+pm[i]+S[1]+pm[j]+S[2]+pm[k]+S[3]+"=7")
break
else:
continue
break
else:
continue
break【参考】
多重ループからのbreakについて体系的に解説されている。
https://note.nkmk.me/python-break-nested-loops/
ABC080 C – Shopping Street(ビット全探索・論理演算)
C – Shopping Street (atcoder.jp)
- 0, 1で表されるデータを扱う→2進数を使うと良さげ。
- 文字列として受け取った2進数 f を数値に変換する。
- bit全探索で、10^10-1以下のすべての2進数に対して、各 f とのand演算をすればよい。
- ABC045 C – たくさんの数式と共通点がある。
N = int(input())
F = []
for _ in range(N):
f = input()
f = f.replace(' ','')
# 文字列として受け取った2進数を、10進数の数値型として扱う
F.append(int(f, 2))
P = [list(map(int, input().split())) for _ in range(N)]
# 0以外の、10桁の全ての2進数を用意する
ans = -10**9
for i in range(1,1<<10):
tmp = 0
for j, f in enumerate(F):
idx = bin(i&f).count("1")
tmp += P[j][idx]
ans = max(ans, tmp)
print(ans)ABC081 C – Not so Diverse(カウント・二分探索)
C – Not so Diverse (atcoder.jp)
- dict型またはCounterで数字の種類ごとにカウント。
- カウント結果のvaluesを昇順にソートする。
- valueの小さいほうから、他の数字に書き換えていけばよい。「書き換える」は、①数字の種類-1, ②ans += 数字の数で実装できる。
import collections
N, K = map(int, input().split())
A = list(map(int, input().split()))
counter = collections.Counter(A)
# 辞書型のメソッドkeys(), values(), items()も使える
nums = sorted(counter.values())
ans = 0
length = len(nums)
for n in nums:
if length <= K:
break
else:
ans += n
length -= 1
print(ans)ABC082 C – Good Sequence(カウント・ソート)
C – Good Sequence (atcoder.jp)
Counter()を使えばよい。それぞれの数字に対して
- 個数が過剰な時は過剰な文だけ取り除く。
- 個数が足りない時はすべて取り除く。
import collections
N = int(input())
A = list(map(int, input().split()))
counter = collections.Counter(A)
ans = 0
for key, value in counter.items():
# 個数が過剰な時
if key < value:
ans += value - key
# 個数が足りないとき
elif key > value:
ans += value
print(ans)ABC083 C – Multiple Gift(計算量)
C – Multiple Gift (atcoder.jp)
Xの初期値をAとし、何回2倍にできるかを数えればよい。
X, Y = map(int, input().split())
A = X
length = 1
while True:
A *= 2
if A <= Y:
length += 1
else:
break
print(length)ABC084C – Special Trains(分類無し)
C – Special Trains (atcoder.jp)
- 問題文が複雑だが、具体例を使って考えれば理解できる。
- 始発時刻と発車時刻を考慮して、それぞれの駅から終着駅まで行くのにかかる最短時間を求めるという問題。
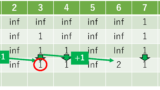
開通式開始を時刻0とする。駅 j に時刻 t に到着したとき、駅 j + 1へ向かう列車に乗れる(最も早い)時刻を求めるという問題に帰着する。
- t <= Sj の場合、駅 j の始発列車は未だ駅 j を出発できないので、乗車時刻はSj。
- t > Sj の場合、以下の2つの場合が考えられる。
- (1)駅 j での待ち時間が発生しない場合。すなわち t %Fj == 0
このとき、駅 j 到着後待ち時間0で乗車できるので、乗車時刻は t - (2)駅 j での待ち時間が発生する場合。すなわち t % Fj != 0
このとき、駅 j 到着後 t’ = Fj – t%Fj の待ち時間が発生し、乗車時刻は t + t’
ここまで場合分けができれば、あとはコードに落とし込むだけである。
N = int(input())
C = [0]*(N-1)
S = [0]*(N-1)
F = [0]*(N-1)
for i in range(N-1):
C[i], S[i], F[i] = map(int, input().split())
# 駅 i を出発する場合
for i in range(N):
if i == N-1:
print(0)
break
t = 0
# 駅 i で初乗車後、駅 j で乗り継ぐ
for j in range(i, N-1):
if t <= S[j]:
t = S[j] + C[j]
else:
if t%F[j] == 0:
t += C[j]
else:
t += F[j] - t%F[j] + C[j]
print(t)ABC085 C – Otoshidama(計算量)
- 紙幣の合計枚数の制約があるので、10000円札に関するループと、5000円札に関するループの2重r-プで十分。
- 1000円札の枚数を N – i – j で表すと、負になる可能性があるので、条件式 N >= i+j を付けたす必要があることに注意。
- 2重ループから抜け出す方法を知っておく必要がある。
N, Y = map(int, input().split())
flag = False
for i in range(Y//10000 + 1):
for j in range(Y//5000 + 1):
if i*10000 + j*5000 + (N-i-j)*1000 == Y and N >= i+j:
print(i, j, N-i-j)
flag = True
break
else:
continue
break
if not flag:
print("-1 -1 -1")ABC086 C – Traveling(4方向への移動)
- 時刻 \(t_i\) に \((x_i, y_i)\) に存在できるための条件を考える。
- \(t_{i-1}\) からの時刻の変化\(\Delta t = t_i – t_{i-1}\)が、\(x\) 座標の変位の大きさ・\(y\) 座標の変位の大きさの和 \(\Delta r = |x_i – x_{i-1}| + |y_i – y_{i-1}|\) より小さければ、どうやっても \((x_i, y_i)\) にたどり着くことはできない。
- \(\Delta r \le \Delta t\) を満たす場合、その場にとどまることができないため、\(\Delta r , \Delta t\)の差が2の倍数であれば \((x_i, y_i)\) にたどり着くことができ、そうでなければたどり着くことは不可能。
N = int(input())
def check(dt, dx, dy):
if dt < dx + dy:
return False
else:
if (dt - (dx + dy)) % 2 == 0:
return True
else:
return False
inputs = [list(map(int, input().split())) for _ in range(N)]
t_pre, x_pre, y_pre = 0, 0, 0
for i in range(N):
t, x, y = inputs[i][0], inputs[i][1], inputs[i][2]
dt = t - t_pre
dx = abs(x-x_pre)
dy = abs(y-y_pre)
# Trueなら更新
if check(dt, dx, dy):
t_pre = t
x_pre = x
y_pre = y
# Falseなら終了
else:
print("No")
break
if i == N-1:
print("Yes")ABC087 C – Candies(計算量)
どこで降りるかで和が決まることにさえ気づけば、O(N)で実装できる。
N = int(input())
A = [list(map(int, input().split())) for _ in range(2)]
ans = 0
# どこで下に降りるかはN通り
for j in range(N):
# j 列目で降りるときの和
tot = sum(A[0][:j+1]) + sum(A[1][j:])
ans = max(tot, ans)
print(ans)ABC088 C – Takahashi’s Information(計算量)
C – Takahashi’s Information (atcoder.jp)
- (1) 3*3行列Cの各要素の値は決まっているので、a1の考えられる範囲で全探索すれば、行列Cの(1, 1)より、b1が自動的に決定する。
- (2) a1, b1・行列Cの(1, 2), (2, 2), (2, 1)より、a2, b2が自動的に決定する。
- (3) a1, b1, a2, b2と行列Cの(1, 3), (2, 3), (3, 3), (3, 1), (3, 2)より、a3, b3が自動的に決定する。
- (1)~(3)において、自動的に決定する値が条件を満たしているかをチェックしていけばよい。
C = [list(map(int, input().split())) for _ in range(3)]
# a1 + b1 == C11を満たすa1, b1を全探索
flag = False
for i in range(C[0][0]+1):
a1 = i
b1 = C[0][0] - i
# b1を定義できなければ終了
if b1 < 0:
continue
# a2, b2に関する条件式
# a2 + b2 == C22
if (C[1][0] - b1) + (C[0][1] - a1) == C[1][1]:
a2 = C[1][0] - b1
b2 = C[0][1] - a1
# a2, b2のいづれかでも定義できなければ終了
else:
continue
# a3, b3に関する条件式
if (C[2][0] - b1) == (C[2][1] - b2) and \
(C[0][2] - a1) == (C[1][2] - a2) and \
(C[2][0] - b1) + (C[0][2] - a1) == C[2][2]:
print("Yes")
flag = True
break
if not flag:
print("No")ABC089 C – March(重複無しの組み合わせ)
- MARCHのうち1文字を先頭に持つ文字列の数をcollections.Counter()で取得。
- 解を得るのに重複無しの組み合わせが必要なので、itertools.combinations。
以下の使い方があることを覚えておきたい。
| 組み合わせor順列 | 重複の有無 | コード |
| 順列 | あり | itertools.product(iter, num) |
| 順列 | なし | itertools.permutations(iter, num) |
| 組み合わせ | あり | itertools.combinations_with_replacement(iter, num) |
| 組み合わせ | なし | itertools.combinations(iter, num) |
import collections
import itertools
N = int(input())
# 先頭の文字だけを使用する
S = [input()[0] for _ in range(N)]
counter = collections.Counter(S)
# 先頭文字の全組み合わせを取得
pairs = itertools.combinations("MARCH", 3)
ans = 0
for pair in pairs:
for i in range(3):
if i == 0:
tmp = counter[pair[i]]
else:
tmp *= counter[pair[i]]
ans += tmp
print(ans)ABC090 C – Flip,Flip, and Flip……(計算量)
C – Flip,Flip, and Flip…… (atcoder.jp)
- 周囲を囲むカードが奇数枚の場合、偶数回裏返される。よって、最終的に表になる。
- 周囲を囲むカードが偶数枚の場合、奇数回裏返される。よって、最終的に裏になる。
- “周囲を囲む”を扱うには、いくつかの場合分けが必要。
N, M= map(int, input().split())
if N == 1 and M == 1:
print(1)
elif N == 1:
print(M-2)
elif M == 1:
print(N-2)
else:
print((N-2)*(M-2))ABC091 C – 2D Plane 2N Points(多次元配列の複数キーでのソート)
C – 2D Plane 2N Points (atcoder.jp)
- x座標に対するソートと、y座標に対するソートの2重のソートを行いたい。
- 「多次元リストを複数キーでソートする」を行えばよい。
- ソート完了後、bisectも2重で行えばよい。
from bisect import bisect_left
N = int(input())
A = [list(map(int, input().split())) for _ in range(N)]
sorted_A = sorted(A, key=lambda x:(x[0], x[1]))
Ax = [0]*N
Ay = [0]*N
for i in range(N):
Ax[i], Ay[i] = sorted_A[i][0], sorted_A[i][1]
B = [list(map(int, input().split())) for _ in range(N)]
sorted_B = sorted(B, key=lambda x:(x[0], x[1]))
Bx = [0]*N
By = [0]*N
for i in range(N):
Bx[i], By[i] = sorted_B[i][0], sorted_B[i][1]
# 赤い点iの座標Aiより、x, yどちらも大きい青い点の数を求める
ans = 0
# x座標の最も小さいBの要素Bxi, Byiに対し
# 条件を満たす中で最もy座標の大きいAの要素をペアとする
for i in range(N):
# 条件を満たすAxの境界
idx = bisect_left(Ax, Bx[i])
# x座標の条件を満たすAy[:idx]の中で、y座標の条件を満たす最大のy座標を探す
if idx != 0:
Axy = [ay for ay in Ay[:idx] if ay < By[i]]
if len(Axy) != 0:
ay_max = max(Axy)
# BiとペアにするAの要素
idxy = Ay.index(ay_max)
ans += 1
del Ax[idxy]
del Ay[idxy]
print(ans)if idx != 0:
Axy = [ay for ay in Ay[:idx] if ay < By[i]]
if len(Axy) != 0:の部分に注意。1つ目のif文では、Bx[i]より小さいAxの要素の有無を判定している。それをクリアした場合、2つ目のif文で、By[i]より小さいAyの要素の有無を判定している。私は、特に2つ目の条件を忘れて、何度もREになってしまった。
【参考】
[Python] 多次元リストを複数キーでソートする – Qiita
ABC092 C – Traveling Plan(移動距離)
C – Traveling Plan (atcoder.jp)
- まずは移動に掛かる距離を全区間で求め、その総和を求めておく。
- 各地点に立ち寄らない場合に、変化する移動距離を求める関数changeを作成。
- 各地点jについて、立ち寄らない場合の総移動距離を出力していく。
N = int(input())
A = list(map(int, input().split()))
# 各地点間の距離を記録していく
dist = []
for i in range(N+1):
if i == 0:
dist.append(abs(A[0]))
elif i < N:
dist.append(abs(A[i] - A[i-1]))
else:
dist.append(abs(A[N-1]))
# a, b, cの順の時、bに行かない場合にかかる距離の変化
def change(a, b, c):
if min(a, c) <= b <= max(a, c):
return 0
else:
return - (abs(b - a) + abs(c - b)) + abs(c - a)
tot = sum(dist)
# 地点jを訪れない場合
for j in range(N):
if j == 0:
print(tot + change(0, A[j], A[j+1]))
elif j < N - 1:
print(tot + change(A[j-1], A[j], A[j+1]))
else:
print(tot + change(A[j-1], A[j], 0))ABC093 C – Same Integers(偶奇の利用)
AtCoder Beginner Contest 093 – AtCoder
- A, B, Cが同じになる最小の値Mは、sum(A, B, C)と3*max(A, B, C)の偶奇が等しいとき、M = max(A, B, C)となる。偶奇が異なる時、M = max(A, B, C) + 1となる。
- 目標のMが分かれば、あとは、必要な操作の回数を求めればよい。
- 3つの数の内、Mと偶奇が等しいものの個数で操作方法が変わる。
(1)3つの数の偶奇がMと等しいとき、それぞれに2を足していけばよい。
(2)2つの数n偶奇がMと等しいことはあり得ない。
(3)1つの数の偶奇がMと等しいとき、1回だけ残りの数に1を足し、その後(1)を行う。
abc = list(map(int, input().split()))
if max(abc) % 2 == sum(abc) % 2:
M = max(abc)
else:
M = max(abc) + 1
# 必要な回数を求める
ans = 0
for i in abc:
ans += (M-i)//2
if all([i%2 == M%2 for i in abc]):
print(ans)
else:
print(ans + 1)ABC094 C – Many Medians(ソート)
- キーを選択してソートする。
N = int(input())
X = list(map(int, input().split()))
sorted_X = sorted(X)
iX = [[i, x] for i, x in enumerate(X)]
iX = sorted(iX, key=lambda x:(x[1]))
for i in range(N):
if i < N//2:
iX[i].append(sorted_X[N//2])
else:
iX[i].append(sorted_X[N//2-1])
iXB = sorted(iX)
for i in range(N):
print(iXB[i][2])ABC095 C – Half and Half(計算量)
C – Half and Half (atcoder.jp)
- まず、A, Bを1つずつ購入するよりもA, Bセットで買った方がお得な時、min(X, Y)個のセットを購入する。
- 残りの必要なA, Bの個数X, Yを更新する。セットで買った場合、A, Bの内少ない方が0となる。セットで買う方が高い場合、X, Yは変化しない。
- A, Bの片方だけが欲しいとき、セットで買った方が安いかどうかを考える。
- 残りの必要なA, Bの個数X, Yを更新する。
- 最後に単品で買うべき分を総額に足して出力。
A, B, C, X, Y = map(int, input().split())
tot = 0
if A + B > 2*C:
XY = min(X, Y)
tot += 2*C*XY
X -= XY
Y -= XY
if A > 2*C and X > 0:
tot += X*2*C
X = 0
elif B > 2*C and Y > 0:
tot += Y*2*C
Y = 0
print(tot + A*X + B*Y)ABC096 C – Grid Repainting 2(グリッド)
C – Grid Repainting 2 (atcoder.jp)
- マス目上に並んだ各#が、上下左右少なくとも1つの#と隣接しているかを判定すればよい。
H, W = map(int, input().split())
grid = [input() for _ in range(H)]
def check(h, w):
cnt = 0
# 黒の時
if grid[h][w] == "#":
# 上から時計回りにチェック
if h >= 1 and grid[h-1][w] == "#":
cnt += 1
if w <= W-2 and grid[h][w+1] == "#":
cnt += 1
if h <= H-2 and grid[h+1][w] == "#":
cnt += 1
if w >= 1 and grid[h][w-1] == "#":
cnt += 1
if cnt:
return True
else:
return False
# 白の時
else:
return True
ans = 0
for h in range(H):
for w in range(W):
ans += check(h, w)
print("Yes" if ans==H*W else "No")ABC097 C – K-th Substring(ソート)
C – K-th Substring (atcoder.jp)
S = input()
K = int(input())
strings = []
for s in range(len(S)):
for k in range(1,K+1):
sub = S[s:s+k]
if sub not in strings:
strings.append(sub)
print(sorted(strings)[K-1])ABC098 C – Attention(総和の利用)
- 答えをn_preとすると、初期値は最も左にいる人に注目した場合に方向転換する人、すなわち左から2番目以降にある”E”の数とする。
- 注目する人を左から順に1人ずつずらしていく。
- 注目する人の向きと、注目する人より一つ左の人の向きを考慮し、答えを更新していく。
N = int(input())
S = input()
n_pre = S[1:].count("E")
num = n_pre
for i in range(N-1):
# 現在地
if S[i+1] == "E":
num -= 1
if S[i] == "W":
num += 1
# 1つ前の値と現在の値を比較
n_pre = min(n_pre, num)
print(n_pre)ABC099 C – Strange Bank(個数制限なし部分和問題)
- DPで解くことのできる個数制限なし部分和問題に落とし込める。
- 何回かの操作によって、0, 1, 2, … N-1, N円までの各金額を実現することができるかを更新していけばよい。
DP(動的計画法)とは?部分和問題とは?という場合は、以下の記事で徹底解説しています。
N = int(input())
A = []
# 操作で足しうるすべての数を列挙
for n in [6, 9]:
n0 = n
while n <= N:
A.append(n)
n *= n0
dp = [[0]*(N+1) for _ in range(len(A)+1)]
for i in range(N+1):
dp[0][i] = i
for i in range(1, len(A)+1):
for j in range(N+1):
ref = dp[i-1][j]
if A[i-1] > j:
dp[i][j] = ref
else:
ref_back = dp[i-1][j - A[i-1]]
ref_back_curr = dp[i][j - A[i-1]]
dp[i][j] = min(ref, ref_back+1, ref_back_curr+1)
print(dp[len(A)][N])次の記事




コメント