【動的計画法】DPで最安値問題を解く（Python）

最安値問題 アルゴリズム
2022.05.26
スポンサーリンク

動的計画法（DP）の練習として、最安値問題は適切な難易度の問題だ。本記事では、例題を通してDPアルゴリズムの基礎を理解していく。

スポンサーリンク

最安値を達成するには：単品とセットどちらをいくつ買えばよいか

問題

八百屋にて、りんご1個が a 円で、りんご2個が b 円で売られています。りんごの買い方を工夫したとき、n 個のりんごを手に入れるために必要な金額の最小値はいくらでしょうか。なお、買い方を工夫した結果、買ったりんごが n+1 個以上になってもよいものとします。

引用元：https://paiza.jp/works/mondai/dp_primer/dp_primer_apples_step0

部分和問題としての考え方

リンゴ i 個（1 ≦ i ≦ n-1）を買う時の最安値が、すべての i について判明しているとする。
すなわち、

・リンゴ１個を買う時の最安値 = dp[1]
・リンゴ２個を買う時の最安値 = dp[2]
…
・リンゴ i 個を買う時の最安値 = dp[i]
…
・リンゴ n-1 個を買う時の最安値 = dp[n-1]

が全て分かっているとする。この時、n 個のリンゴを最安値で買う方法の候補は２通りある。

  • n – 1 個のリンゴを最安値で買ってから、1個をa円で購入する。
  • n – 2 個のリンゴを最安値で買ってから、2個をb円で購入する。
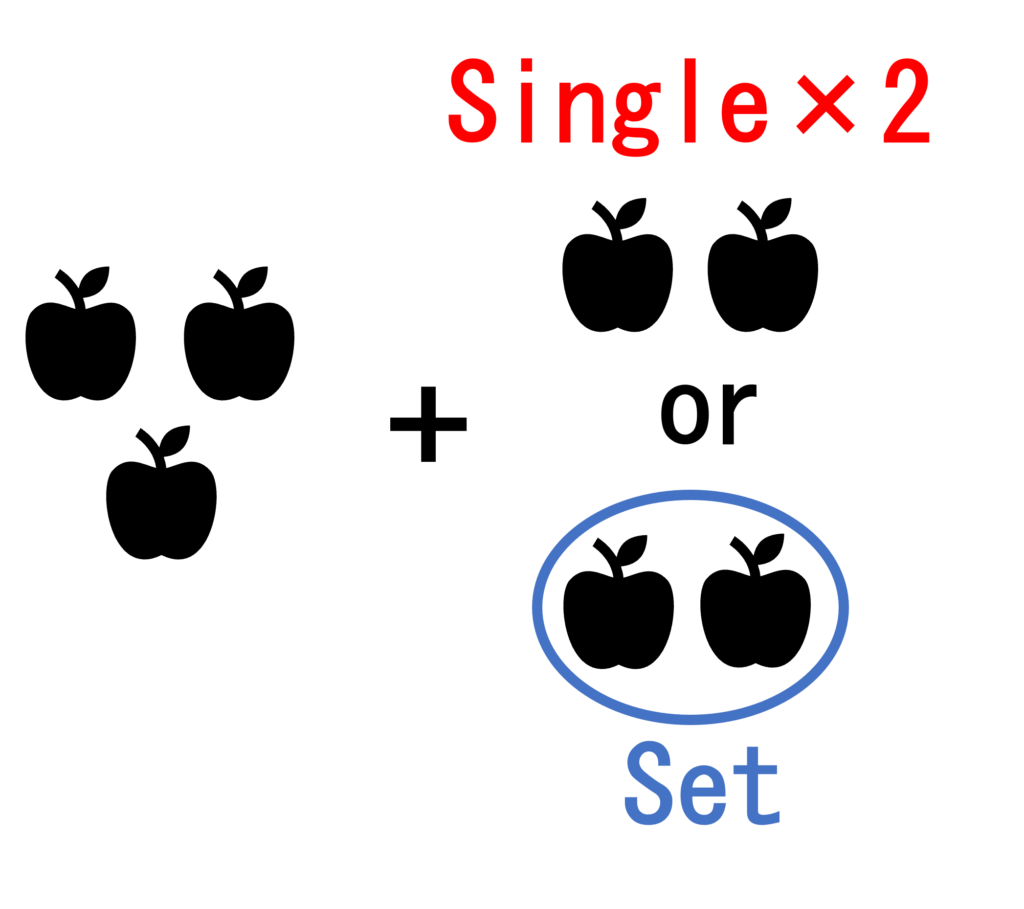
りんごで最安値問題をイメージする
５個のリンゴを最安値で買いたいとき、３個は最安値で手に入れているとする。後の２個は、どのように買えばよいだろうか。

上記の内、安くなる方が、n 個を買う際の最安値である。これらのアイデアを漸化式に落とし込む。

漸化式で考える

  • n – 1 個のリンゴを最安値 dp[n-1] 円で買ってから、1個をa円で購入する場合
    金額は dp[n-1] + a 円となる。
  • n – 2 個のリンゴを最安値で買ってから、2個をb円で購入する場合
    金額は dp[n-2] + b 円となる。

これらの内、最終的な値段が安くなる方が採用されるので、漸化式は次のように書ける。

$$dp[n] = min(dp[n-1] + a , \ dp[n-2] + b)$$

また、初期値は\(dp[0]=0, \ dp[1] = a\)であることは明らかである。０個買う際の最安値は当然 0 円であるし、１個買う際の最安値は a 円しかありえない。２個買う際は、買い方が２通り存在するが、この先は dp に任せておけばよい。では、コードを書いてみよう。

コード例

n, a, b = map(int, input().split())
dp = [0]*(n+1)
dp[0] = 0
dp[1] = a

for i in range(2, n+1):
    dp[i] = min(dp[i-1]+a, dp[i-2]+b)

print(dp[n])
スポンサーリンク

最安値を達成するには：ちょうど n 個を買う方法が無いとき

問題

八百屋にて、りんご2個が a 円で、りんご5個が b 円で売られています。
りんごの買い方を工夫したとき、n 個のりんごを手に入れるために必要な金額の最小値はいくらでしょうか。なお、買い方を工夫した結果、買ったりんごが n+1 個以上になってもよいものとします。

引用元：https://paiza.jp/works/mondai/dp_primer/dp_primer_apples_step1

部分和問題としての考え方

ぱっと見、全問と同じ解き方を採用できそうである。しかし、１つの難点がある。
リンゴをちょうど１個、３個買う方法が無いことである。（この問題では、４個以上をちょうどの個数買うことが可能である。しかし、次の問題では２個セットor５個セットとは限らないため、本問よりもちょうどの個数で買うことができないケースが多い）

i 個買う時の最安値は、

  • ちょうど i 個買う時の最安値
  • i 個より多く買う時の最安値

のうち安い方である。ここで、２つに分けるのは面倒なので、次のようにまとめてしまおう。

i 個買う時の最安値は、i 個以上買うときの最安値である。

引用元のヒントでも述べているように、dp は dp[n] までではなく、余裕をもって dp[n+4] 程度まで計算しておく必要があることに注意する。ちょうど n 個を買う組み合わせが無く、「n -1 個買う時の最安値 + 5 個の値段」が最安値になる可能性が無いとも言えないからである。

漸化式で考える

ちょうどの個数を買うことができないパターンは取り合えず置いておき、まずは、ちょうど買える個数についてだけ、最安値を求める。

  • n – 2 個のリンゴを最安値 dp[n-2] 円で買ってから、2個をa円で購入する場合
    金額は dp[n-2] + a 円となる。
  • n – 5 個のリンゴを最安値で買ってから、5個をb円で購入する場合
    金額は dp[n-5] + b 円となる。

これらの内、最終的な値段が安くなる方が採用されるので、漸化式は次のように書ける。

$$dp[n] = min(dp[n-2] + a , \ dp[n-5] + b)$$

ちょうど買えない個数についての最安値の補完は、下のコード例で解説する。

コード例

n, a, b = map(int, input().split())
dp = [10000001]*(n+5)
dp[0] = 0

for i in range(2,n+5):
    dp[i] = min(dp[i-2] + a, dp[i-5] + b)
for i in range(1,n+1):
    dp[i] = min(dp[i:i+5])

print(dp[n])

ここで、比較min()を正しく処理するために、適当に大きな数でdpの中身を初期化しておく。

ちょうど買えない個数についての補完は、

for i in range(1,n+1):
    dp[i] = min(dp[i:i+5])

で行う。dp[i]が漸化式で求まっていれば（ちょうど買える個数なら）、値はそのままであるし、求まっていなければ（ちょうど買うことができない個数なら）、i 個より多く買う中での最安値が採用される。

別解

すべての i についてdp[i]を求めなくても良いので、以下のコードも正解である。
こちらの方が無駄がない。

n, a, b = map(int, input().split())
dp = [10000001] * (n + 5)
dp[0] = 0

for i in range(2, n + 5):
    if i >= 2:
        dp[i] = min(dp[i], dp[i - 2] + a)
    if i >= 5:
        dp[i] = min(dp[i], dp[i - 5] + b)

print(min(dp[n:]))
スポンサーリンク

ちょうど n 個を買う方法が無いとき（３通りの分岐がある）

問題

八百屋にて、りんご x 個が a 円で、りんご y 個が b 円で、りんご z 個が c 円で売られています。
りんごの買い方を工夫したとき、n 個のりんごを手に入れるために必要な金額の最小値はいくらでしょうか。なお、買い方を工夫した結果、買ったりんごが n+1 個以上になってもよいものとします。

引用元：https://paiza.jp/works/mondai/dp_primer/dp_primer_apples_boss

これは、全問と全く同じ問題なので、全問のコード内にて、３つ目のz個のセットについての記述を加え、適切な箇所をx, y, zに書き換えればよい。

コード例

n, x, a, y, b, z, c = map(int, input().split())

dp = [1000*10000]*(n+z)
dp[0] = 0

for i in range(x, n+z):
    if i >= x:
        dp[i] = min(dp[i], dp[i-x] + a)
    if i >= y:
        dp[i] = min(dp[i], dp[i-y] + b)
    if i >= z:
        dp[i] = min(dp[i], dp[i-z] + c)

print(min(dp[n:]))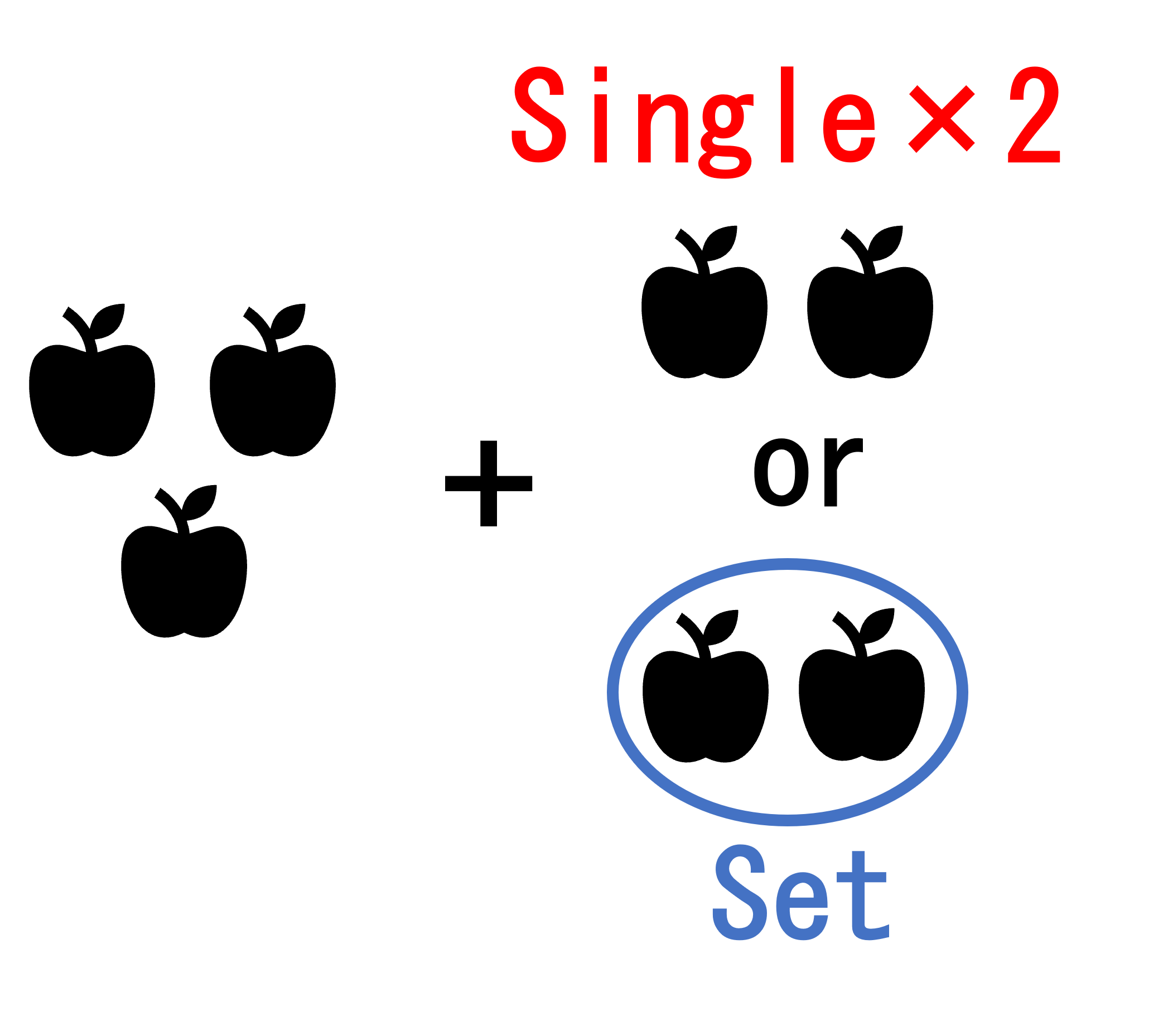

コメント