本記事では、グラフの連結性の判定について、Pythonでの実装例を紹介します。数学的要素をやや含む問題ですので、もう少しシンプルなABC075 C-Bridge の解説もご覧ください。
問題は→D – Circumferences (atcoder.jp)
N個の円(中心の座標・半径)と、2つの点(始点・終点)が与えられたとき始点から円周に沿って移動し、終点にたどり着くことができるかを判定する問題。
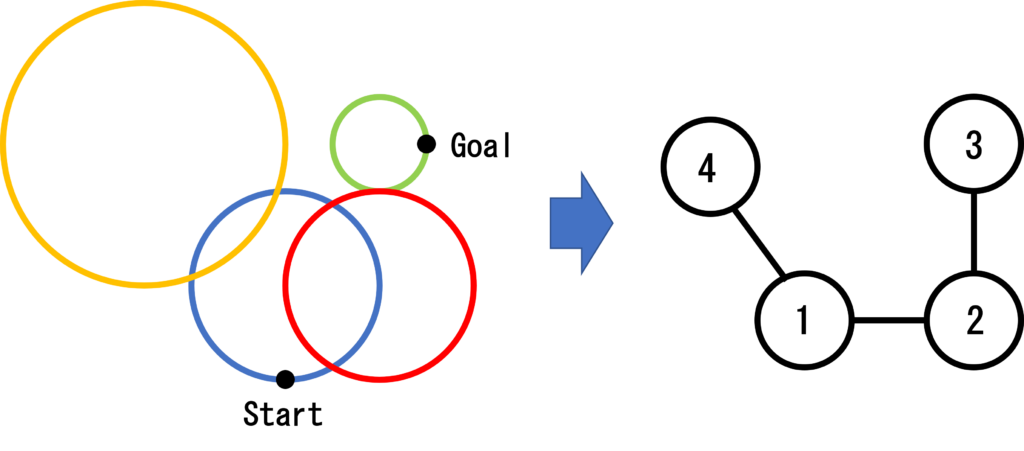
- 円群の交わりの関係をグラフの連結性に変換。
→円周が交わる条件を判定する。また、始点と終点はどの円周に属するか? - グラフを隣接行列で表現する。
- 始点から終点まで行くためには、始点の属する円と、終点の属する円が無向グラフによって連結されている必要がある。
- 深さ優先探索(DFS)でグラフの連結性を判定する。
【円が交わる条件】
2つの円のそれぞれの半径を \(r_1, r_2\) とします。2つの円の中心間の距離を \(d\) とすると、2つの円が少なくとも1点で交わるための条件は、
$$r_2-r_1 \le d \le r_1 + r_2 \ \ (r_1 < r_2)$$
です。しかし、2つの問題があります。
・直接距離を用いる場合、√を使うため誤差が生じてしまう。
・また、\(r_1, r_2\) の大小関係を考慮する必要がある。
ここで、距離の2乗で比較を行えば、どちらも解決できます。すなわち、
$$(r_2-r_1)^2 \le d \le (r_1 + r_2)^2 $$
これで、\(r_1, r_2\) の大小関係も気にせずに実装することができます。
【連結性の判定】
(無向)グラフ上で、ある頂点(ノード)sから、辺(エッジ)をたどり、目的とする頂点Tに行き着くことは可能かを判定します。例えば、「N個の島と、それらにまたがるM個の橋が存在するとき、島Sから橋を渡って島Tにたどり着けるか?」という問題は、グラフの連結性判定で解くことができます。
- 始点や終点が複数の円にまたがる場合、どの円に属すると判断するか?
→DFSで、結局そのようなすべての円を訪問するので、適当に選んでよい(最後に点が属すると判定された円など) - 一部のテストケースでWAやREになった。
→Python3で提出するとWAになった。PyPy3で提出すべし。
→デフォルトの再帰回数上限(10^3程度)ではREになってしまうテストケースが8つ程あったので、sys.setrecursionlimit()で増やしておく。
# 再帰回数の上限を設定する
import sys
sys.setrecursionlimit(10**6)
N = int(input())
sx, sy, tx, ty = map(int, input().split())
# 隣接行列の生成
matrix = [[0]*N for _ in range(N)]
# 入力された座標を格納するリスト
c = []
start = -1
goal = -1
# 連結判定とグラフ(隣接行列)への変換
for i in range(N):
x, y, r = map(int, input().split())
if i > 0:
for j in range(len(c)):
if (r-c[j][2])**2 <= (x-c[j][0])**2 + (y-c[j][1])**2 <= (r+c[j][2])**2:
matrix[i][j] = 1
matrix[j][i] = 1
if (x-sx)**2+(y-sy)**2==r**2:
start = i
if (x-tx)**2+(y-ty)**2==r**2:
goal = i
c.append([x,y,r])
# 深さ優先探索ですべての頂点が連結されているか判定
def dfs(v):
# 頂点 v を訪問済みにする
visited[v] = 1
for v2 in range(N):
# 頂点 v と頂点 v2 との結合が無い場合
if matrix[v][v2] == 0:
continue
# v2 は訪問済みの場合
if visited[v2] == 1:
continue
dfs(v2)
# 訪問履歴
visited = [0] * N
# 頂点visited[start]を始点とし、各頂点を可能な限り訪問する
dfs(start)
# 終点に訪問したかどうか判定
if visited[goal]==1:
print("Yes")
else:
print("No")【参考】
公式解説動画
ABC075 C-Bridge 公式解説(当サイトではPythonでの解説記事を掲載しています(下))



コメント