【電気双極子】1. 電場中で電気双極子に働く力

1. 電機双極子と電気双極子モーメントの定義

電気双極子とは, 同じ大きさで負号が異なる２つの電荷の対である.

また, 電機双極子の特徴を表した, 次のベクトル量を電気双極子モーメントと呼ぶ. ベクトル$\mathbf{d}$の意味については, 2. の冒頭で説明する.

電気双極子モーメント
$$\mathbf{p} \equiv q\mathbf{d}$$

２つの電荷の電荷量と, 距離さえあれば, 電機双極子の特徴を表せる. しかし, なぜ, わざわざこのような物理量を定義するのか？以下では, 電場中に置いた電機双極子に働く力と, 電気双極子モーメントとの関係について考える.

2. 一様な電場中で電気双極子に働く力

長さ$d$で質量を無視できる棒の両端に, 大きさの等しい正負の電荷$\pm q$が付いているとする. この系が一様な電場$\mathbf{E}$の中にある時, 棒に働く力を考える.

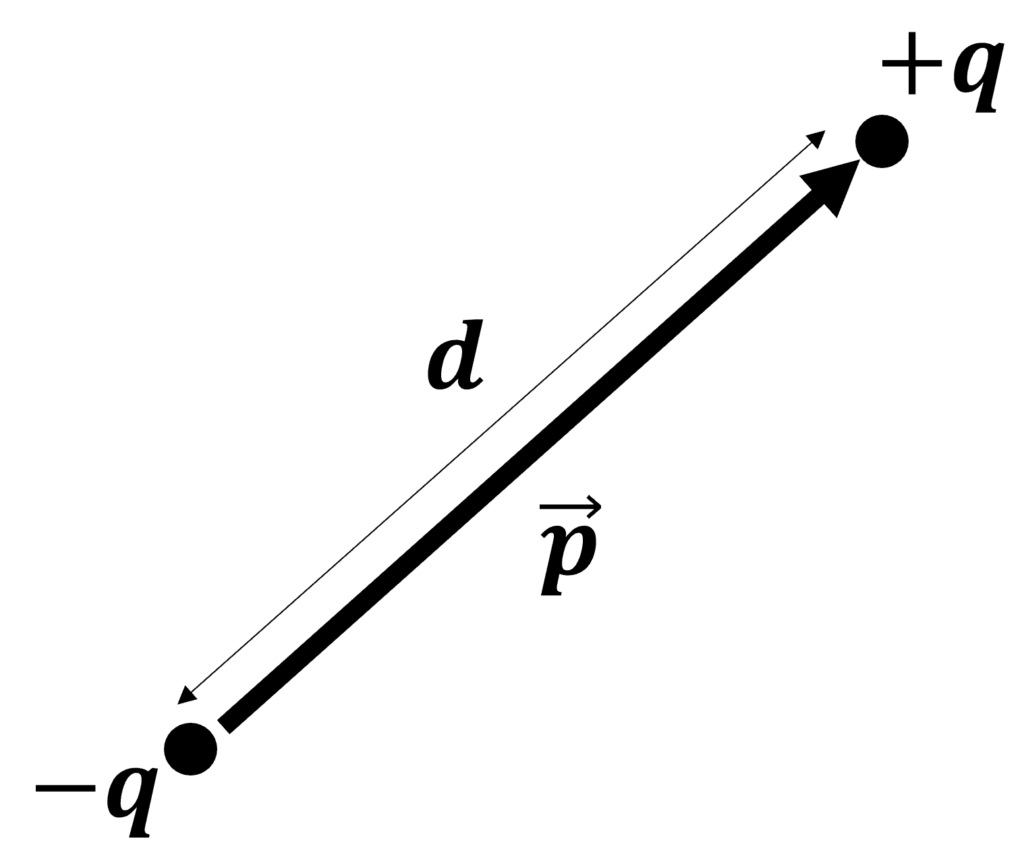
電場は空間的に一様であるから, 棒の両端の電荷に対し, 大きさの等しい逆向きの力が働く. これは, すなわち, 棒を回転させる偶力に他ならない.

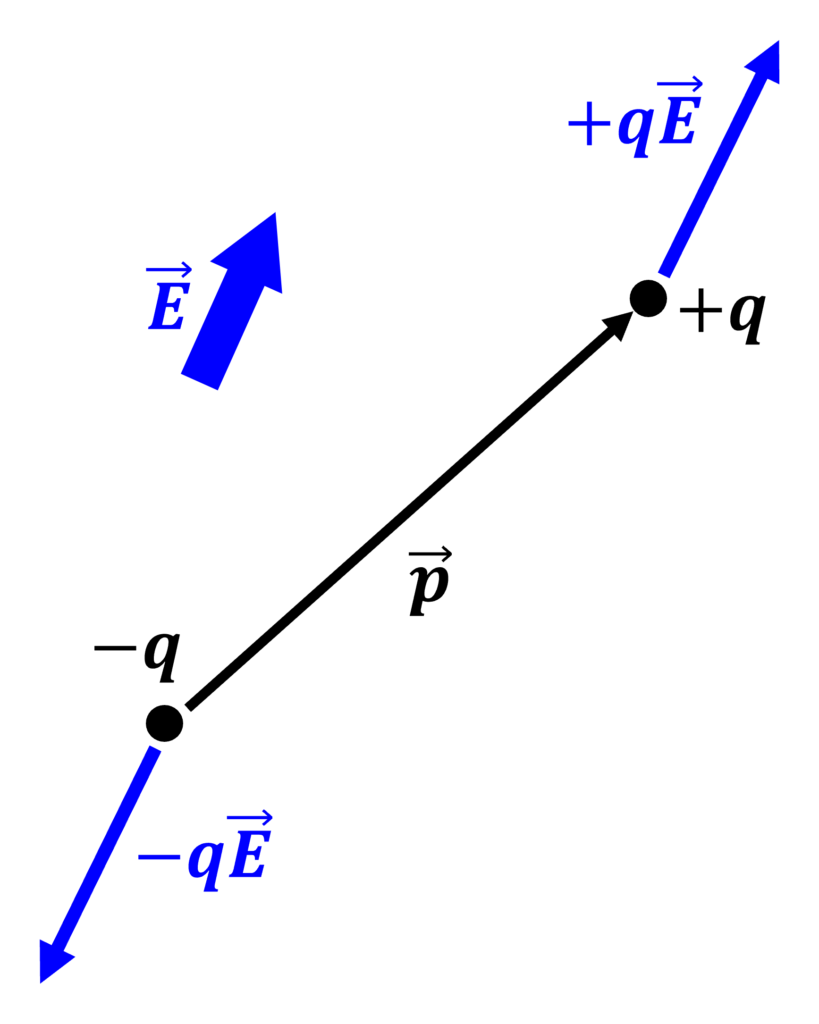
ここで, 負の電荷 ⇒ 正の電荷の向きで, 大きさが$d$のベクトル$\mathbf{d}$を定義すると, 棒に働く偶力のモーメント（トルク）は,

$$\mathbf{N} = \mathbf{d} \times q\mathbf{E}$$

となる. ここで, 電気双極子モーメントの定義を用いれば,

$$\mathbf{N} = \mathbf{p} \times \mathbf{E}$$

と, 双極子に働く力を, より簡潔に表現することができる.

3. 非一様の任意の電場中で電気双極子に働く力

現実の電場は, 必ずしも, 空間的に一様ではない. それはちょうど, 川の流れのようである. 川岸, 川の中央や川底といった異なる場所では, 流速（ベクトル）も異なる. 偶然同じ大きさの流速でも, 流れが同じ向きを向いている確率は極めて低いと思われる. このように, 空間的に非一様な電場の中に置かれた双極子に働く力を考えよう.

上図のように, 系の中心を$\mathbf{r}$とし,

$\mathbf{r} + \mathbf{d}$に位置する点電荷$q$
$\mathbf{r} – \mathbf{d}$に位置する点電荷$-q$

によって電気双極子モーメント$\mathbf{p}$が作られるとする.

今, 電場$\mathbf{E}(\mathbf{r})$は, 場所に依存するので,

電荷$+q$が受ける力は, $\mathbf{F}_+ = q\mathbf{E}(\mathbf{r} + \mathbf{d})$

電荷$-q$が受ける力は, $\mathbf{F}_- = – q\mathbf{E}(\mathbf{r} – \mathbf{d})$

したがって, 電機双極子が受ける力は,

\begin{align*}
\mathbf{F} &= \mathbf{F}_+ + \mathbf{F}_-\\
&= q\left\{\mathbf{E}(\mathbf{r} + \mathbf{d}) – \mathbf{E}(\mathbf{r} – \mathbf{d})\right\}
\end{align*}

ここで, 各点電荷の位置での電場を, 系の中心における電場を用いて表せる.

$$\mathbf{E}(\mathbf{r} + \mathbf{d}) = \mathbf{E}(\mathbf{r}) + (\mathbf{d}\cdot \nabla)\mathbf{E}(\mathbf{r})$$

$$\mathbf{E}(\mathbf{r} \ – \ \mathbf{d}) = \mathbf{E}(\mathbf{r}) \ – \ (\mathbf{d}\cdot \nabla)\mathbf{E}(\mathbf{r})$$

理由
位置$\mathbf{r}$から微小距離$\mathbf{dr}$だけ離れた場所における電場の各成分は, $\mathbf{r}$周りのテイラー展開を用いて, 次のように表せる.
\begin{align*}
E_x(\mathbf{r} + \mathbf{dr}) &= E_x(x + dx, y + dy, z + dz)\\
&= \displaystyle \sum_{n = 0}^{\infty} \frac{1}{n!}\left(dx\partial_x+ dy\partial_y+ dz\partial_z\right)^n E_x(x, y, z)\\
&\cong E_x(x, y, z) + \left(dx\partial_x+ dy\partial_y+ dz\partial_z\right) E_x(x, y, z)
\end{align*}
同様に
$$E_y(\mathbf{r} + \mathbf{dr}) = E_y(x, y, z) + \left(dx\partial_x+dy\partial_y+dz\partial_z\right) E_y(x, y, z)$$
$$E_y(\mathbf{r} + \mathbf{dr}) = E_y(x, y, z) + \left(dx\partial_x+dy\partial_y+dz\partial_z\right) E_y(x, y, z)$$
ここで, 偏微分は$\partial_x = \frac{\partial}{\partial x}$のように省略した.

３成分を１つの式にまとめて書くと
\begin{align*}
\mathbf{E}(\mathbf{r} + \mathbf{dr}) &= \mathbf{E}(\mathbf{r}) + \left(dx\partial_x+dy\partial_y+dz\partial_z\right)\mathbf{E}(\mathbf{r})\\
&= \mathbf{E}(\mathbf{r}) + (\mathbf{dr}\cdot\nabla) \mathbf{E}(\mathbf{r})
\end{align*}
が成り立つ.

したがって, $\mathbf{dr} \rightarrow \mathbf{d}$と書き換えれば,
$$\mathbf{E}(\mathbf{r} + \mathbf{d}) = \mathbf{E}(\mathbf{r}) + (\mathbf{d}\cdot \nabla) \mathbf{E}(\mathbf{r})$$
と表すことができる.