電気双極子モーメント\(\mathbf{p}\)がz軸の正の向きを向いて, 原点Oに置かれているとき, 点P\((x, y, z)\)における電位\(\phi (x, y, z)\)および, 電場\(\mathbf{E}(x, y, z)\)を求めよ.
[解]
1. 電気双極子による電位
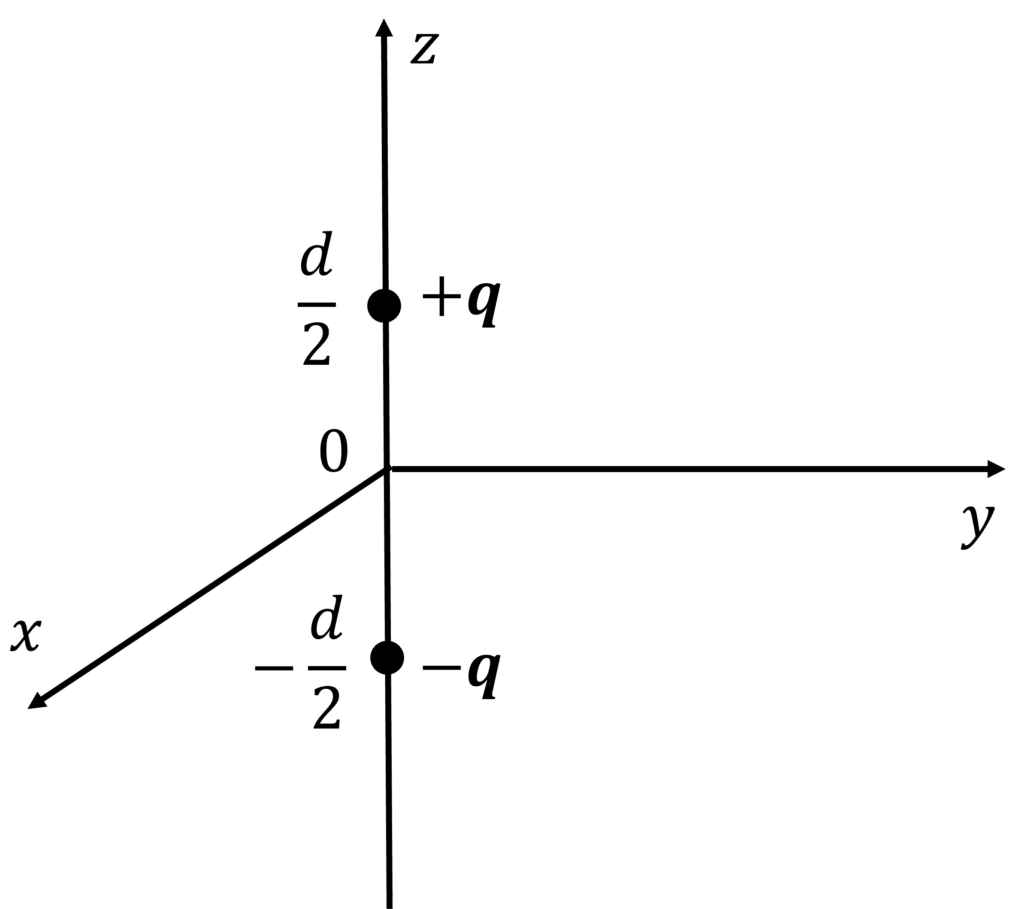
上図のように電荷を配置したとき, \(d \ll r\)を満たす, 系から十分離れた任意の場所\(\mathbf{r} = (x, y, z)\)における電位は
で求めたように,
$$\phi (\mathbf{r}) = \frac{p}{4\pi\varepsilon_0}\frac{z}{r^2} \ …(1)$$
である.
電気双極子モーメントが任意の方向を向いている場合
ここで, 電気双極子モーメント\(\mathbf{p} = q\mathbf{d}\)が, 任意の方向を向きうるベクトルであると考えると
\begin{align*}
\phi (\mathbf{r}) &= \frac{1}{4\pi\varepsilon_0}\frac{(0, 0, qd)\cdot (0, 0, z)}{r^3}\\
&= \frac{1}{4\pi\varepsilon_0}\frac{q\mathbf{d}\cdot\mathbf{r}}{r^3}\\
&= \frac{1}{4\pi\varepsilon_0}\frac{\mathbf{p}\cdot\mathbf{r}}{r^3}
\end{align*}
これにより, 次の公式を得ることができる.
一般の方向を向いた電気双極子モーメント\(\mathbf{p}\)による電位(ポテンシャル)
$$\phi (\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\frac{\mathbf{p}\cdot\mathbf{r}}{|\mathbf{r}|^3}$$
今回は直交座標(デカルト座標)系を用いて計算したが, 極座標を用いても, 電位について同様の結果を得ることができる. これについては, 次の記事を参照されたい.
2. 電気双極子モーメントのつくる電場
電気双極子から十分に離れた場所では, 電位を簡単な式で書けた.
ここで, 静電場と電位の関係式
$$\mathbf{E} = – \nabla \phi (\mathbf{r}) \ …(2)$$
に, 上で求めた(1)式の電位を代入すると
\begin{align*}
E_x &= – \frac{\partial \phi}{\partial x}\\
&= \frac{p}{4\pi \varepsilon_0}\frac{3xz}{r^5}
\end{align*}
\begin{align*}
E_y &= – \frac{\partial \phi}{\partial y}\\
&= \frac{p}{4\pi \varepsilon_0}\frac{3yz}{r^5}
\end{align*}
\begin{align*}
E_z &= – \frac{\partial \phi}{\partial z}\\
&= -\frac{p}{4\pi \varepsilon_0}\frac{1}{r^3} + \frac{p}{4\pi \varepsilon_0}\frac{z^2}{r^5}\\
&= \frac{p}{4\pi \varepsilon_0}\frac{3z^2 – r^2}{r^5}\\
&= \frac{p}{4\pi \varepsilon_0}\frac{2z^2 – x^2 – y^2}{r^5}
\end{align*}
ここで, 連鎖律を使い, 各偏微分を次のように計算した.
\begin{align*}
\frac{\partial}{\partial x}\left(\frac{1}{r^3}\right) &= – \frac{3}{2}\cdot \frac{2x}{(x^2 + y^2 + z^2)^{5/2}}\\
&= -\frac{3x}{r^5}
\end{align*}
同様に
$$\frac{\partial}{\partial y}\left(\frac{1}{r^3}\right) = – \frac{3y}{r^5}$$
$$\frac{\partial}{\partial z}\left(\frac{1}{r^3}\right) = – \frac{3z}{r^5}$$
電気双極子モーメントが任意の方向を向いている場合
z軸方向に限らず, 一般の方向を向いた, 原点を中心に配置された電気双極子モーメント\(\mathbf{p}\)による電位は,
$$\phi (\mathbf{r} = \frac{1}{4\pi\varepsilon_0})\frac{\mathbf{p}\cdot\mathbf{r}}{|\mathbf{r}|^3} \ …(3)$$
と表せるのであった. では, \(\mathbf{p}\)のx, y成分が0とは限らないときの電場の表式を求めてみよう. 以下の計算過程では, ベクトルの内積が重要となる.
(3)を, (2)に代入し, 電場の各成分を計算する.
\begin{align*}
E_x &= -\frac{\partial \phi}{\partial x}\\
&= – \frac{1}{4\pi \varepsilon_0}\left\{\frac{1}{r^3}\frac{\partial (\mathbf{p}\cdot\mathbf{r})}{\partial x} + (\mathbf{p}\cdot\mathbf{r})\frac{\partial}{\partial x}\left(\frac{1}{r^3}\right)\right\}\\
&= – \frac{1}{4\pi \varepsilon_0}\left\{\frac{1}{r^3}\left(\mathbf{r}\cdot\frac{\partial \mathbf{p}}{\partial x} + \mathbf{p}\cdot\frac{\partial \mathbf{r}}{\partial x}\right) + (\mathbf{p}\cdot\mathbf{r})\frac{-3x}{r^5}\right\}\\
&= – \frac{1}{4\pi \varepsilon_0}\frac{1}{r^3}\left\{(p_x, p_y, p_z)\cdot (1, 0, 0) – \frac{3(\mathbf{p}\cdot\mathbf{r})x}{r^2}\right\}\\
&= – \frac{1}{4\pi \varepsilon_0}\frac{1}{r^3}\left\{p_x – \frac{3(\mathbf{p}\cdot\mathbf{r})x}{r^2}\right\}
\end{align*}
同様に
\begin{align*}
E_y &= – \frac{\partial \phi}{\partial y}\\
&= – \frac{1}{4\pi \varepsilon_0}\frac{1}{r^3}\left\{p_x – \frac{3(\mathbf{p}\cdot\mathbf{r})y}{r^2}\right\}
\end{align*}
\begin{align*}
E_y &= – \frac{\partial \phi}{\partial z}\\
&= – \frac{1}{4\pi \varepsilon_0}\frac{1}{r^3}\left\{p_x – \frac{3(\mathbf{p}\cdot\mathbf{r})z}{r^2}\right\}
\end{align*}
以上の各成分の結果をまとめると, 次のように整理できる.
電気双極子(モーメント)のつくる電場
$$\mathbf{E}(\mathbf{r}) = – \frac{1}{4\pi \varepsilon_0}\frac{1}{r^3}\left\{\mathbf{p} – \frac{3(\mathbf{p}\cdot\mathbf{r})\cdot\mathbf{r}}{r^2}\right\}$$





コメント