k最近傍法の概要
k最近傍法(k-Nearest Neighbor algorithm, k-NN)は、教師あり学習に分類される機械学習アルゴリズムである。分類問題に用いられる、非常にシンプルな手法である。
既にクラスが判明しているデータ点(訓練データ)が分布しているとき、新たなデータ点(テストデータ)が与えられることを考える。k最近傍法では、新たなデータ点から、最も近いk個の点を見て、それらの多数決によって、新たなデータ点のクラスを予測する。
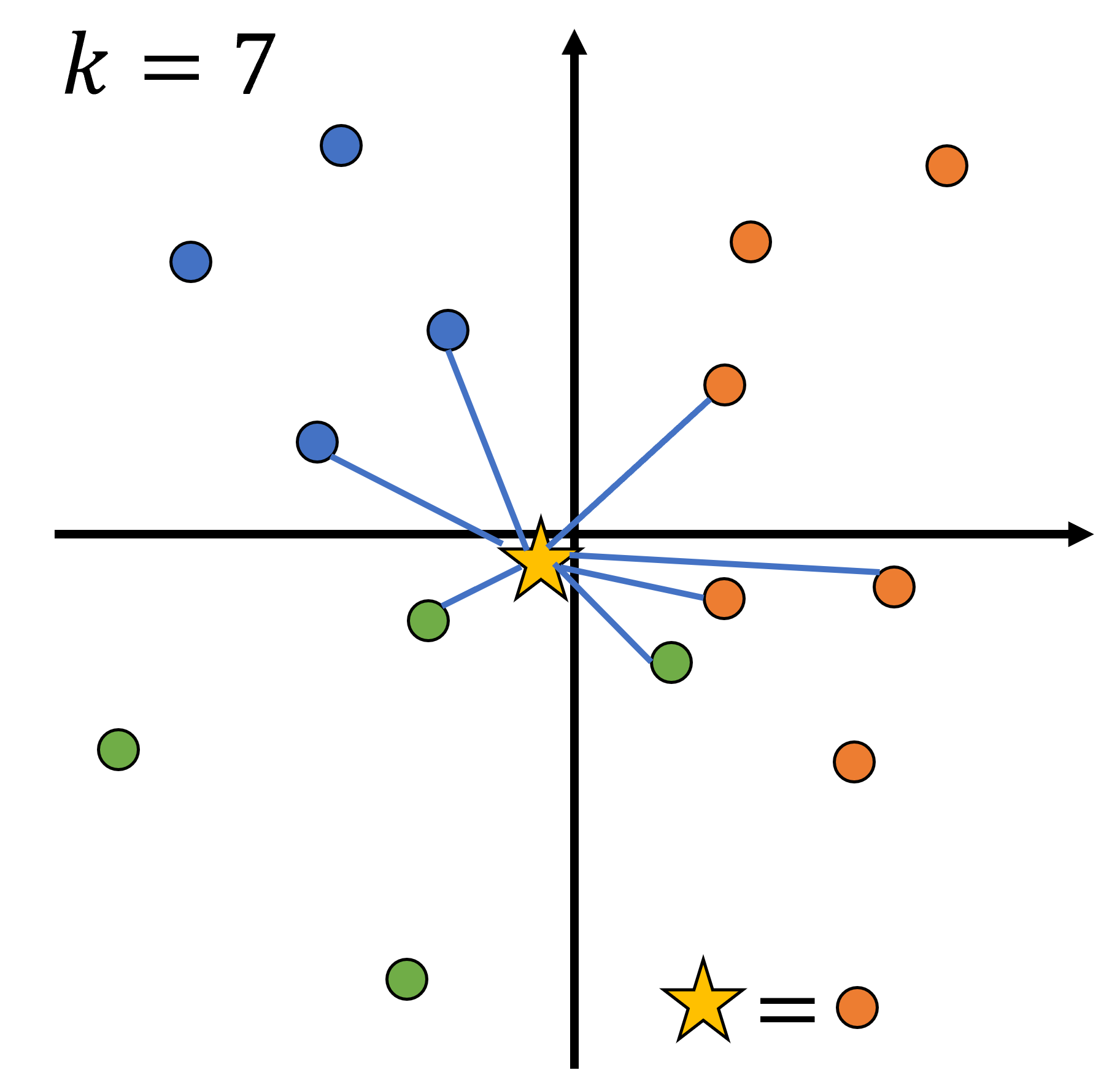
簡単な例を用いてk最近傍法を理解しよう。まず、下図のように、青、橙、緑というクラスを持つ点が存在する。各点には、2次元空間上の座標が与えられている。そこに、クラスが分からない点(☆)が与えられる。この点は、どのクラスに分類されるだろうか。
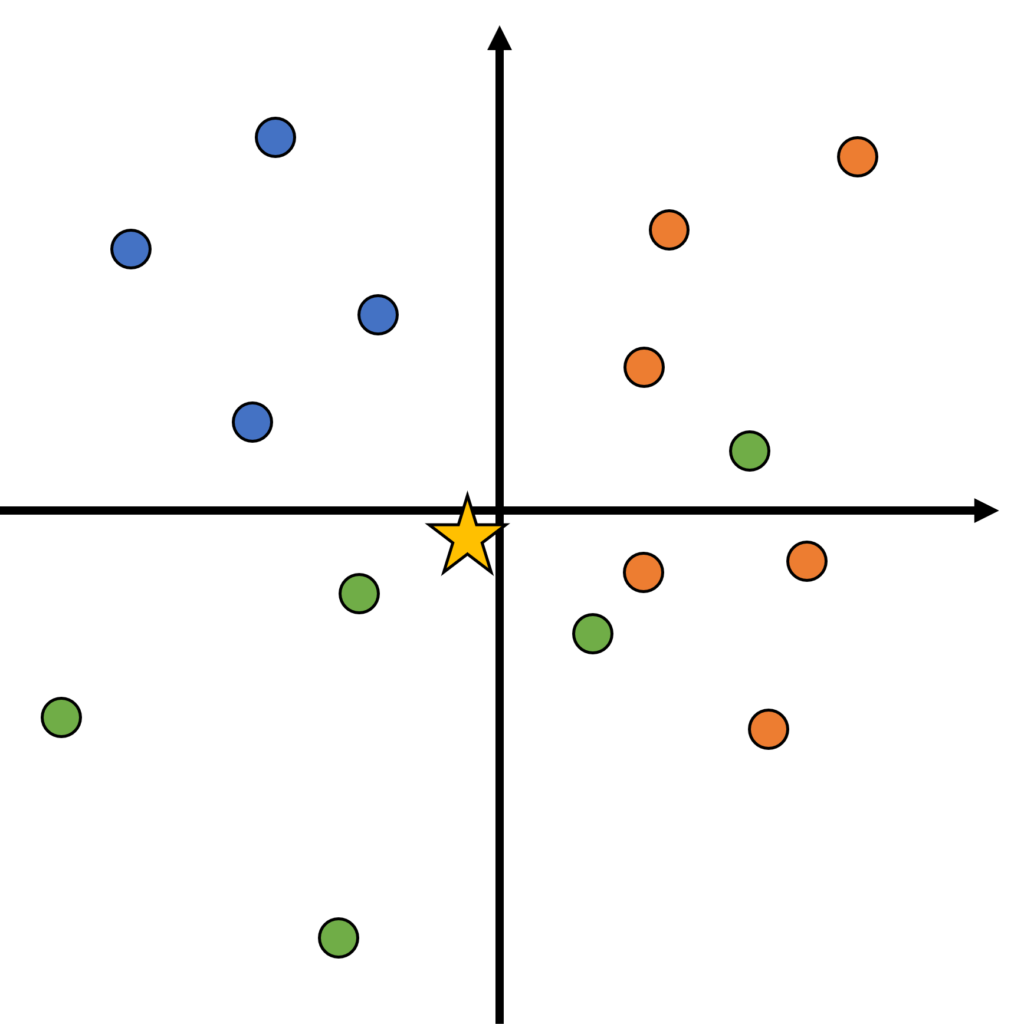
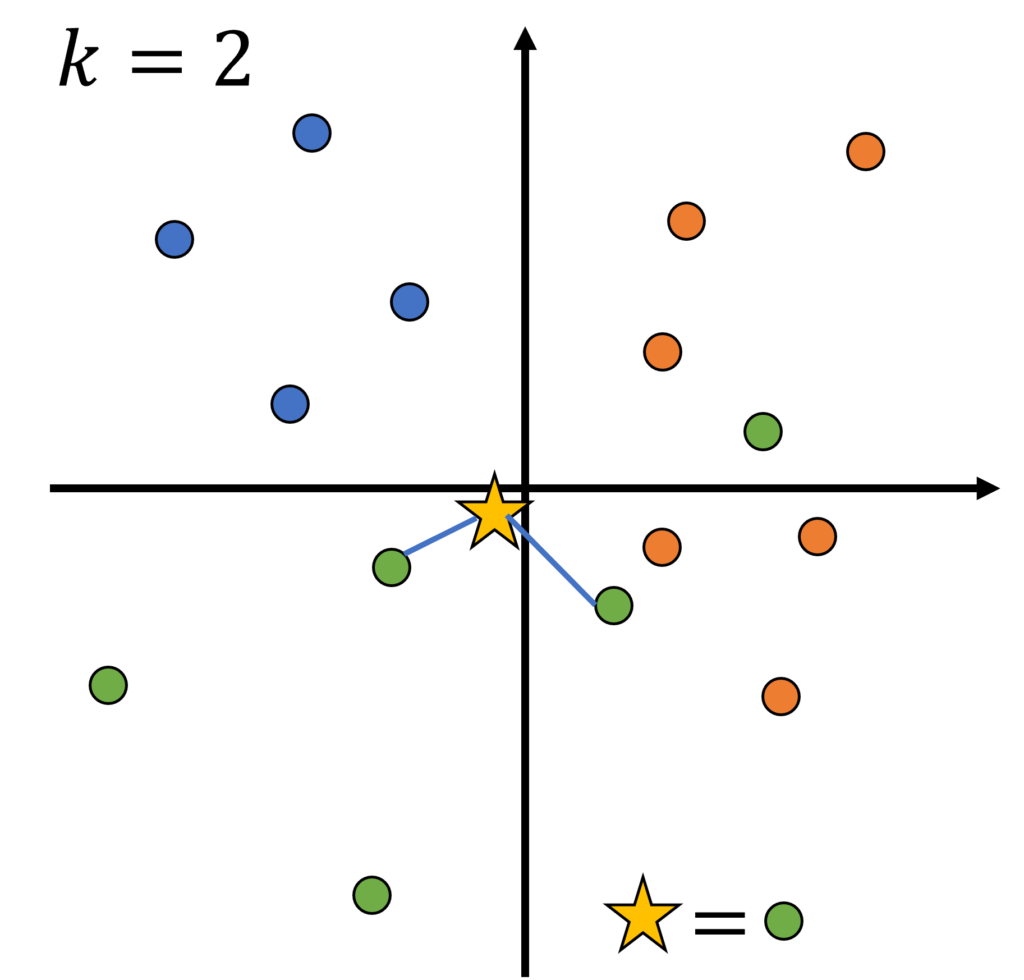
まず、k=2、すなわち新たなデータ点から、最も近い2個の点を見て、それらの多数決によって、新たなデータ点のクラスを予測する。最も近い2点は緑であるから、テストデータは緑だと予測される。
次に、k=7、すなわち新たなデータ点から、最も近い7個の点を見て、それらの多数決によって、新たなデータ点のクラスを予測する。最も近い7点は青×2、橙×3、緑×2であるから、テストデータは橙だと予測される。
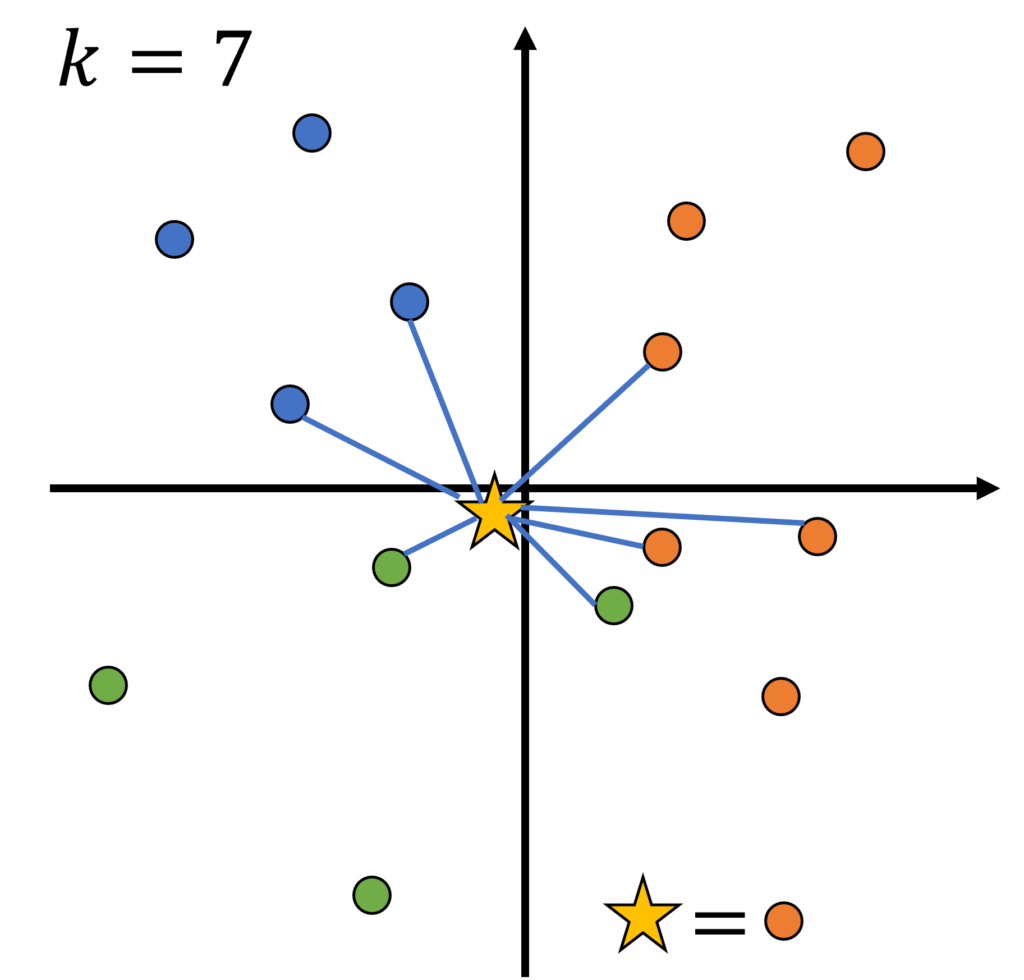
kをどのように設定するかは任意である。今回の場合、橙の数が最も多いので、kを大きくすれば橙にクラス分けされやすくなってしまう。逆にkが小さすぎても、テストデータのクラスの推定結果は座標に強く依存してしまう。
コードを書いて実装する
ここでは、過去6日分の気温・湿度と、その日の私の体調(good or bad)を訓練データとして与え、とある4日間の気温と湿度から、それらの日の体調を予測することを行ってみる。
※以下でのコメントでは目的変数を「ラベル」と呼んでいるが、上記の「クラス」と同じ意味である。
import scipy.spatial.distance as distance
import scipy.stats as stats
import numpy as np
# k-NNクラスを実装
class knn:
def __init__(self, k, metric):
self.k = k
self.metric = metric
# テストデータと訓練データ間の距離を計算し、近いk点を求めるメソッド
def neighbors(self, X_test, X_train):
"""
Parameters
----------
X_test : array-like
ラベルを推定したいテストデータ.
X_train : array-like
ラベルが判明している訓練用データ.
k : int
最近傍のk個のラベルを用いて多数決を行う.
metric : string
距離関数の種類.ユークリッド距離は、通常の2点間の距離を与える.
Returns
-------
neighbors_index : array-like
列方向について、0-k-1番目に距離が小さい点のインデックスを抽出した配列
行方向はX_test, 列方向はX_trainに対応
"""
metric = self.metric
k = self.k
# len(X_test)行 len(X_test)列 の配列を出力.
dist = distance.cdist(X_test, X_train, metric)
neighbors_index = np.argpartition(dist, k)[:,:k]
return neighbors_index
# 予測するためのメソッド
def predict(self, X_test, X_train, y):
"""
Parameters
----------
X_test : array-like
ラベルを推定したいテストデータ.
X_train : array-like
ラベルが判明している訓練用データ.
y : array-like
X_trainの各点に対応するラベル.
Returns
-------
pred : array-like
推定されたX_testのラベル.
"""
# 最も近いk点のインデックスを抽出
neighbors_index = self.neighbors(X_test, X_train)
# ユニークなラベルの配列unique arrayと, 各データのラベルをunique arrayのインデックスに変換した配列
labels, y_labels = np.unique(y, return_inverse=True)
# stats.modeで最頻値を求める(多数決). _は最頻値のカウント数
label_index, _ = stats.mode(y_labels[neighbors_index], axis=1)
# 軸を指定して要素を取り出す
# ravel()でndarrayを一次元化
pred = labels.take(label_index).ravel()
return pred
# データを生成(各点は[気温、湿度」の組にした)
X_train = np.array([[23.5,44.0],[24.0,40.5],[26.0,25.5],[26.5,42.5],[28.0,50.5],[30.0,43.0]])
X_test = np.array([[22.0,24.5],[25.5,30.0],[27.5,35.0],[29.0, 55.5]])
y = ["good","good","good","good","bad","bad"]
# クラスを呼び出してオブジェクトを生成
kNN = knn(k=2, metric="euclidean")
# 予測を実行
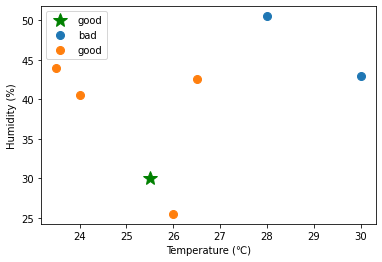
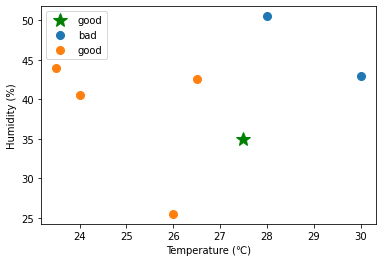
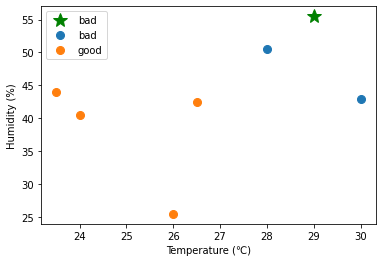
pred = kNN.predict(X_test, X_train, y)予測結果
pred
>> array(['good', 'good', 'good', 'bad'], dtype='<U4')- distance.cdist()を用いて、テストデータの各点\(Xtest_i\)について、\(Xtest_i\)と訓練データのすべての点との距離を求めることができる。
- numpy関数のargsort()等、argが付くと、配置後のインデックスを返すという特徴がある。
- np.argpartition(dist, k)
配列distのなかで、k+1番目に小さい値を持つ要素を基準にし、それより小さい値を持つ要素(1~k番目に小さい要素)は基準の左に、大きい要素は基準より右側に配置される。 - np.unique()
ユニークな要素が格納された配列uが渡される。return_inverse=Trueを指定すると、第二引数として、元の配列に対して、「元の配列の各要素は、uの何番目のインデックスにあたるか」を示した配列が渡される。
予測結果の可視化
# ラベル別に点の座標群を格納するための関数
def group(X, labels):
groups = {}
u, index = np.unique(labels, return_inverse=True)
for i in u:
# ユニークなラベルiに一致するインデックスを取得
members_idx = [j for j, e in enumerate(labels) if e == i]
groups[i] = X[members_idx]
return groups
import matplotlib.pyplot as plt
# グラフ描画
for (s,t) in zip(X_test, pred):
fig, ax = plt.subplots()
ax.plot(s[0] , s[1], marker='*', color="g", linestyle='',ms=15, label=t)
#ax.scatter(x[0] , x[1])
for key, value in group(X_train, y).items():
ax.plot(value[:, 0] , value[:, 1], marker='o', linestyle='', ms=8, label=key)
#ax.scatter(value[:, 0] , value[:, 1])
ax.set_xlabel("Temperature (℃)")
ax.set_ylabel("Humidity (%)")
ax.legend()
plt.show()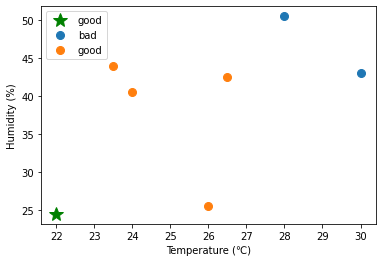

コメント