量子力学や電磁気学で、球対称な形を持つポテンシャルにおける運動を考えるとき、直交座標よりも球座標(極座標)を用いる方が、都合よく計算できる場合が多い。この際、運動方程式に含まれる演算子を球座標(極座標)に変換する必要がある。
そして、その変換はしばしば膨大な計算量を伴う。
量子力学におけるシュレーディンガー方程式に含まれるラプラシアン\(\Delta = \nabla^2\)演算子の球座標表示の導出は、大学の課題として課されることも多い。また、導出過程を通して、座標変換の仕組みを身をもって知ることができるので、一生に一度は取り組んでおくのも悪くない。
ラプラシアン:
(\(\Delta = \nabla^2\ = \frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\))
一般的な変換方法は、直交座標(x, y, z)→球座標(極座標)と直接的である。しかし、たかが偏微分、されど偏微分。真面目に手を動かして計算するには、その量は膨大なものである。学部時代に計算した際は、レポート用紙を20枚以上使用した。よって、苦行を乗り越えたい方には是非上記の座標変換を試してほしい。
しかしここでは、かなり楽な方法を紹介する。
- ステップ1:直交座標(x, y, z)→円筒座標
- ステップ2:円筒座標→球座標(極座標)
一見手間が多いように感じるが、各ステップにおける計算量が少ないため、結果として、全体の計算量は直交座標(x, y, z)→球座標(極座標)の半分くらいになる。また、「円筒座標」という使い慣れない座標系にも触れておくことで、直交座標系以外に、2つの座標系を扱うことになる。よって、座標変換とは何か?を学ぶ機会は2倍になる。結果として、計算量は半分、でも2倍勉強になるというお得な手法なのである(と信じている)。
直交座標から円筒座標表示に変換する
直交座標と円筒座標の関係は、下の図のようになっている。
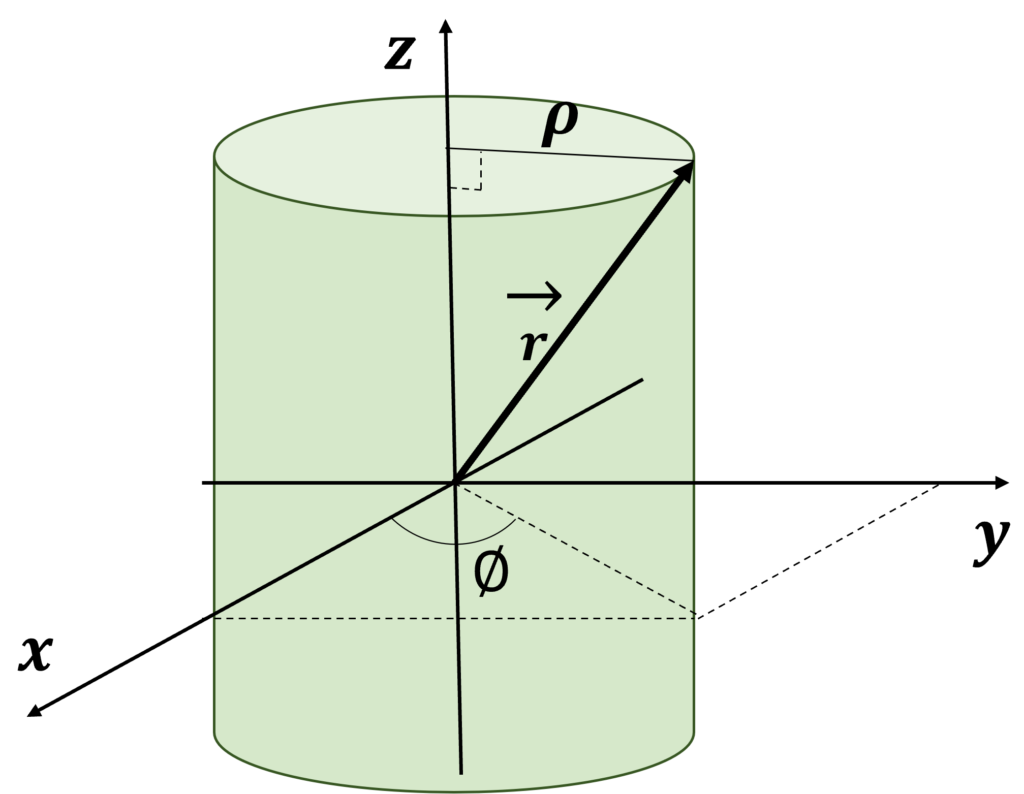
また、数式で表すと、次のような座標の対応関係がある。
\[
\begin{cases}
x &= \rho \mathrm{cos}\phi\\
y &= \rho \mathrm{sin}\phi\\
z &= z
\end{cases}
\]
と変換される。\(\rho = \sqrt{x^2 + y^2}\)であるから
\begin{align*}
\frac{\partial \rho}{\partial x} &= \frac{1}{2}\frac{2x}{\sqrt{x^2 + y^2}}\\
&= \frac{x}{\rho}\\
&= \mathrm{cos}\phi
\end{align*}
\begin{align*}
\frac{\partial \rho}{\partial x} &= \frac{1}{2}\frac{2y}{\sqrt{x^2 + y^2}}\\
&= \frac{y}{\rho}\\
&= \mathrm{sin}\phi
\end{align*}
\(\phi = tan^{-1}\frac{y}{x}\)であるから
\begin{align*}
\frac{\partial \rho}{\partial x} &= \frac{\partial \left(\frac{y}{x}\right)}{\partial x}\frac{\partial}{\partial \left(\frac{y}{x}\right)}\mathrm{tan}^{-1} \left(\frac{y}{x}\right)\\
&= -\frac{y}{x^2}\frac{1}{1+\left(\frac{y}{x}\right)^2}\\
&= -\frac{y}{\rho^2}\\
&= -\frac{\mathrm{sin}\phi}{\rho}
\end{align*}
\begin{align*}
\frac{\partial \rho}{\partial y} &= \frac{\partial \left(\frac{y}{x}\right)}{\partial y}\frac{\partial}{\partial \left(\frac{y}{x}\right)}\mathrm{tan}^{-1} \left(\frac{y}{x}\right)\\
&= \frac{1}{x}\frac{1}{1+\left(\frac{y}{x}\right)^2}\\
&= \frac{x}{\rho^2}\\
&= \frac{\mathrm{cos}\phi}{\rho}
\end{align*}
以上より
\begin{align*}
\frac{\partial}{\partial x} &= \frac{\partial\rho}{\partial x}\frac{\partial}{\partial \rho} + \frac{\partial\phi}{\partial x}\frac{\partial}{\partial \phi}\\
&= \mathrm{cos}\phi\frac{\partial}{\partial \rho} – \frac{\mathrm{sin}\phi}{\rho}\frac{\partial}{\partial \phi}
\end{align*}
\begin{align*}
\frac{\partial}{\partial y} &= \frac{\partial\rho}{\partial y}\frac{\partial}{\partial \rho} + \frac{\partial\phi}{\partial y}\frac{\partial}{\partial \phi}\\
&= \mathrm{sin}\phi\frac{\partial}{\partial \rho} + \frac{\mathrm{cos}\phi}{\rho}\frac{\partial}{\partial \phi}
\end{align*}
これらを用いて
\begin{align*}
\frac{\partial^2}{\partial x^2}&=\frac{\partial\rho}{\partial x}\frac{\partial}{\partial \rho}\left(\mathrm{cos}\phi\frac{\partial}{\partial \rho} – \frac{\mathrm{sin}\phi}{\rho}\frac{\partial}{\partial \phi}\right)\\
& \ \ +\frac{\partial\phi}{\partial x}\frac{\partial}{\partial \phi}\left(\mathrm{cos}\phi\frac{\partial}{\partial \rho} – \frac{\mathrm{sin}\phi}{\rho}\frac{\partial}{\partial \phi}\right)\\
&= \mathrm{cos}\phi\left(\mathrm{cos}\phi\frac{\partial^2}{\partial\rho^2}+\frac{\mathrm{sin}\phi}{\rho^2}\frac{\partial}{\partial \phi} – \frac{\mathrm{sin}\phi}{\rho}\frac{\partial^2}{\partial \phi\partial\rho}\right)\\
& \ \ – \frac{\mathrm{sin}\phi}{\rho}\left(-\mathrm{sin}\phi\frac{\partial}{\partial \rho}+\mathrm{cos}\phi\frac{\partial^2}{\partial\phi\partial\rho}-\frac{\mathrm{cos}\phi}{\rho}\frac{\partial}{\partial\phi} – \frac{\mathrm{sin}\phi}{\rho}\frac{\partial^2}{\partial\phi^2}\right)
\end{align*}
\begin{align*}
\frac{\partial^2}{\partial y^2}&=\frac{\partial\rho}{\partial y}\frac{\partial}{\partial \rho}\left(\mathrm{sin}\phi\frac{\partial}{\partial \rho} + \frac{\mathrm{cos}\phi}{\rho}\frac{\partial}{\partial \phi}\right)\\
& \ \ + \frac{\partial\phi}{\partial x}\frac{\partial}{\partial \phi}\left(\mathrm{sin}\phi\frac{\partial}{\partial \rho} + \frac{\mathrm{cos}\phi}{\rho}\frac{\partial}{\partial \phi}\right)\\
&= \mathrm{sin}\phi\left(\mathrm{sin}\phi\frac{\partial^2}{\partial\rho^2}-\frac{\mathrm{cos}\phi}{\rho^2}\frac{\partial}{\partial \phi} + \frac{\mathrm{cos}\phi}{\rho}\frac{\partial^2}{\partial \phi\partial\rho}\right)\\
& \ \ + \frac{\mathrm{cos}\phi}{\rho}\left(\mathrm{cos}\phi\frac{\partial}{\partial \rho}+\mathrm{sin}\phi\frac{\partial^2}{\partial\phi\partial\rho}-\frac{\mathrm{sin}\phi}{\rho}\frac{\partial}{\partial\phi} + \frac{\mathrm{cos}\phi}{\rho}\frac{\partial^2}{\partial\phi^2}\right)
\end{align*}
よって
$$\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}=\frac{\partial^2}{\partial \rho^2}+\frac{1}{\rho}\frac{\partial}{\partial\rho} + \frac{1}{\rho^2}\frac{\partial^2}{\partial \phi^2}$$
すなわち、円筒座標におけるラプラシアンは
$$\Delta = \frac{\partial^2}{\partial \rho^2}+\frac{1}{\rho}\frac{\partial}{\partial\rho} + \frac{1}{\rho^2}\frac{\partial^2}{\partial \phi^2}+\frac{\partial^2}{\partial z^2}$$
と表される。
円筒座標から球座標表示に変換する
直交座標・円筒座標と球座標の関係は、下の図のようになっている。
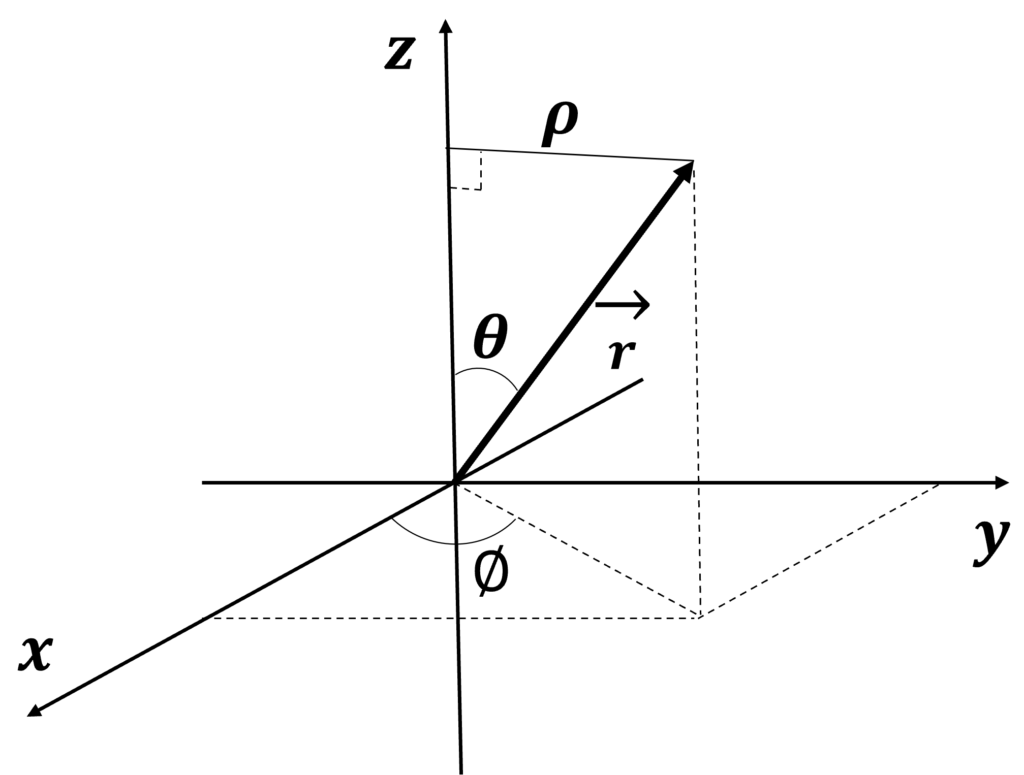
また、数式で表すと、次のような座標の対応関係がある。
\[
\begin{cases}
\rho &= \mathrm{sin}\theta\\
z &= r\mathrm{cos}\theta
\end{cases}
\]
と書ける。すると
\begin{align*}
\frac{\partial r}{\partial \rho} &= \frac{\partial \sqrt{\rho^2+z^2}}{\partial \rho}\\
&= \frac{\rho}{\sqrt{\rho^2+z^2}}\\
&= \mathrm{sin}\theta
\end{align*}
\(\mathrm{tan}\theta = \frac{\rho}{z}\), \(\mathrm{tan}^{-1}\left(\frac{\rho}{z}\right)\)より
\begin{align*}
\frac{\partial \theta}{\partial \rho}&=\frac{\partial\left(\frac{\rho}{z}\right)}{\partial\rho}\frac{\partial}{\partial\left(\frac{\rho}{z}\right)}\mathrm{tan}^{-1}\left(\frac{\rho}{z}\right)\\
&= \frac{1}{z}\frac{1}{1+\left(\frac{\rho}{z}\right)^2}\\
&= \frac{\mathrm{cos}\theta}{r}
\end{align*}
したがって
\begin{align*}
\frac{\partial}{\partial \rho} &= \frac{\partial r}{\partial \rho}\frac{\partial}{\partial r}+\frac{\partial\theta}{\partial \rho}\frac{\partial}{\partial \theta}\\
&= \mathrm{sin}\theta\frac{\partial}{\partial r} + \frac{\mathrm{cos}\theta}{r}\frac{\partial}{\partial \theta}
\end{align*}
\begin{align*}
\frac{\partial^2}{\partial \rho^2} &= \frac{\partial r}{\partial \rho}\frac{\partial}{\partial r}\left(\mathrm{sin}\theta\frac{\partial}{\partial r} + \frac{\mathrm{cos}\theta}{r}\frac{\partial}{\partial \theta}\right)\\
& \ \ + \frac{\partial \theta}{\partial \rho}\frac{\partial}{\partial \theta}\left(\mathrm{sin}\theta\frac{\partial}{\partial r} + \frac{\mathrm{cos}\theta}{r}\frac{\partial}{\partial \theta}\right)\\
&= \mathrm{sin}\theta\left(\mathrm{sin}\theta\frac{\partial^2}{\partial r^2}-\frac{ \mathrm{cos}\theta}{r^2}\frac{\partial}{\partial\theta}+\frac{\mathrm{cos}\theta}{r}\frac{\partial^2}{\partial\theta\partial r}\right)\\
& \ \ + \frac{\mathrm{cos}\theta}{r}\left(-\mathrm{cos}\theta\frac{\partial}{\partial r}+\mathrm{sin}\frac{\partial^2}{\partial r\partial\theta}-\frac{\mathrm{sin}\theta}{r}\frac{\partial}{\partial\theta}+\frac{\mathrm{cos}\theta}{r}\frac{\partial^2}{\partial\theta^2}\right)
\end{align*}
$$\frac{1}{\rho}{\partial}{\partial\rho} = \frac{1}{r\mathrm{sin}\theta}\left(\mathrm{sin}\theta\frac{\partial}{\partial r}+\frac{\mathrm{cos}\theta}{r}\frac{\partial}{\partial\theta}\right)$$
また、zに関する微分は
\begin{align*}
\frac{\partial r}{\partial z}&=\frac{\partial \sqrt{\rho^2+z^2}}{\partial z}\\
&= \frac{z}{\sqrt{\rho^2+z^2}}\\
&= \mathrm{cos}\theta
\end{align*}
\begin{align*}
\frac{\partial \theta}{\partial z}&=\frac{\partial\left(\frac{\rho}{z}\right)}{\partial z}\frac{\partial}{\partial\left(\frac{\rho}{z}\right)}\mathrm{tan}^{-1}\left(\frac{\rho}{z}\right)\\
&= -\frac{\rho}{z^2}\frac{1}{1+\left(\frac{\rho}{z}\right)^2}\\
&= -\frac{\mathrm{sin}\theta}{r}
\end{align*}
$$\frac{\partial}{\partial z} = \mathrm{cos}\theta\frac{\partial}{\partial r}-\frac{\mathrm{sin}\theta}{r}\frac{\partial}{\partial \theta}$$
\begin{align*}
\frac{\partial^2}{\partial z^2}&= \frac{\partial r}{\partial z}\frac{\partial}{\partial r}\left(\mathrm{cos}\theta\frac{\partial}{\partial r}-\frac{\mathrm{sin}\theta}{r}\frac{\partial}{\partial \theta}\right)\\
& \ \ + \frac{\partial\theta}{\partial z}\frac{\partial}{\partial \theta}\left(\mathrm{cos}\theta\frac{\partial}{\partial r}-\frac{\mathrm{sin}\theta}{r}\frac{\partial}{\partial \theta}\right)\\
&= \mathrm{cos}\left(\mathrm{cos}\frac{\partial^2}{\partial r^2}+\frac{\mathrm{sin}\theta}{r^2}\frac{\partial}{\partial \theta}-\frac{\mathrm{sin}\theta}{r}\frac{\partial}{\partial \theta\partial r}\right)\\
& \ \ -\frac{\mathrm{sin}\theta}{r}\left(-\mathrm{sin}\theta\frac{\partial}{\partial r}+\mathrm{cos}\frac{\partial^2}{\partial r\partial\theta}-\frac{\mathrm{cos}\theta}{r}\frac{\partial}{\partial \theta}–\frac{\mathrm{sin}\theta}{r}\frac{\partial^2}{\partial\theta^2}\right)
\end{align*}
以上より
\begin{align*}
\frac{\partial^2}{\partial \rho^2}+\frac{1}{\rho}\frac{\partial}{\partial \rho}+\frac{\partial^2}{\partial z^2}&=\frac{\partial^2}{\partial r^2}+\frac{1}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}\\
& \ \ + \left(\frac{1}{r}\frac{\partial}{\partial r}+\frac{\mathrm{cos}\theta}{r^2\mathrm{sin}\theta}\frac{\partial}{\partial \theta}\right)\\
&= \frac{\partial^2}{\partial r^2}+\frac{2}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}+\frac{\mathrm{cos}\theta}{r^2\mathrm{sin}\theta}\frac{\partial}{\partial \theta}
\end{align*}
ここで、第1式の()の部分は\(\frac{1}{\rho}\frac{\partial}{\partial \rho}\)である。
また
$$\frac{1}{\rho^2}\frac{\partial^2}{\partial\phi^2} = \frac{1}{(r\mathrm{sin}\theta)^2}\frac{\partial^2}{\partial\phi^2}$$
であるから
$$\Delta=\frac{\partial^2}{\partial r^2}+\frac{2}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\frac{\partial^2}{\partial \theta^2}+\frac{\mathrm{cos}\theta}{r^2\mathrm{sin}\theta}\frac{\partial}{\partial \theta}+\frac{1}{(r\mathrm{sin}\theta)^2}\frac{\partial^2}{\partial\phi^2}$$
得られる。すなわち
$$\Delta=\frac{\partial^2}{\partial r^2}+\frac{2}{r}\frac{\partial}{\partial r}+\frac{1}{r^2}\hat{\Lambda}(\theta, \phi)$$
ここで
$$\hat{\Lambda}(\theta, \phi)=\frac{\partial^2}{\partial \theta^2}+\frac{\mathrm{cos}\theta}{\mathrm{sin}\theta}\frac{\partial}{\partial \theta}+\frac{1}{\mathrm{sin}^2\theta}\frac{\partial^2}{\partial\phi^2}$$


コメント