はじめに
先日データ解析をしていて,移動方向に対して直交するベクトルってどうやって求めれば良いんだろう?という疑問が生まれました.
本記事の解説は,「進行方向に直交するベクトルを求める」というタスクへの応用が利く内容となっています.応用例としては,自転する地球上を移動する物体に働く,「コリオリ力」の方向を計算すること等が挙げられます.また,磁場中を移動する電荷に働く「ローレンツ力」も,電荷の進行方向に対して垂直に働く力です.
2次元平面上のベクトルを回転させるには,回転行列という,2×2行列を使います.なお,3次元空間内のベクトルの回転についても回転行列を使うのは同じです.
1. ベクトルの復習
さて,早速本題に入りましょう.
まず,xy平面上に,ベクトル\(\vec{v} = (v_x, v_y)\)が存在するとします.ベクトルの意味をあえて言語化するなら,「x軸方向に距離\(v_x\),y軸方向には距離\(v_y\)進むような,向きと長さを示す矢印」です.速度ベクトルの場合,「単位時間に」という前置きが付き,「単位時間(1秒間)に,x軸方向に距離\(v_x\),y軸方向には距離\(v_y\)進むような,向きと長さを示す矢印」であると言えます.
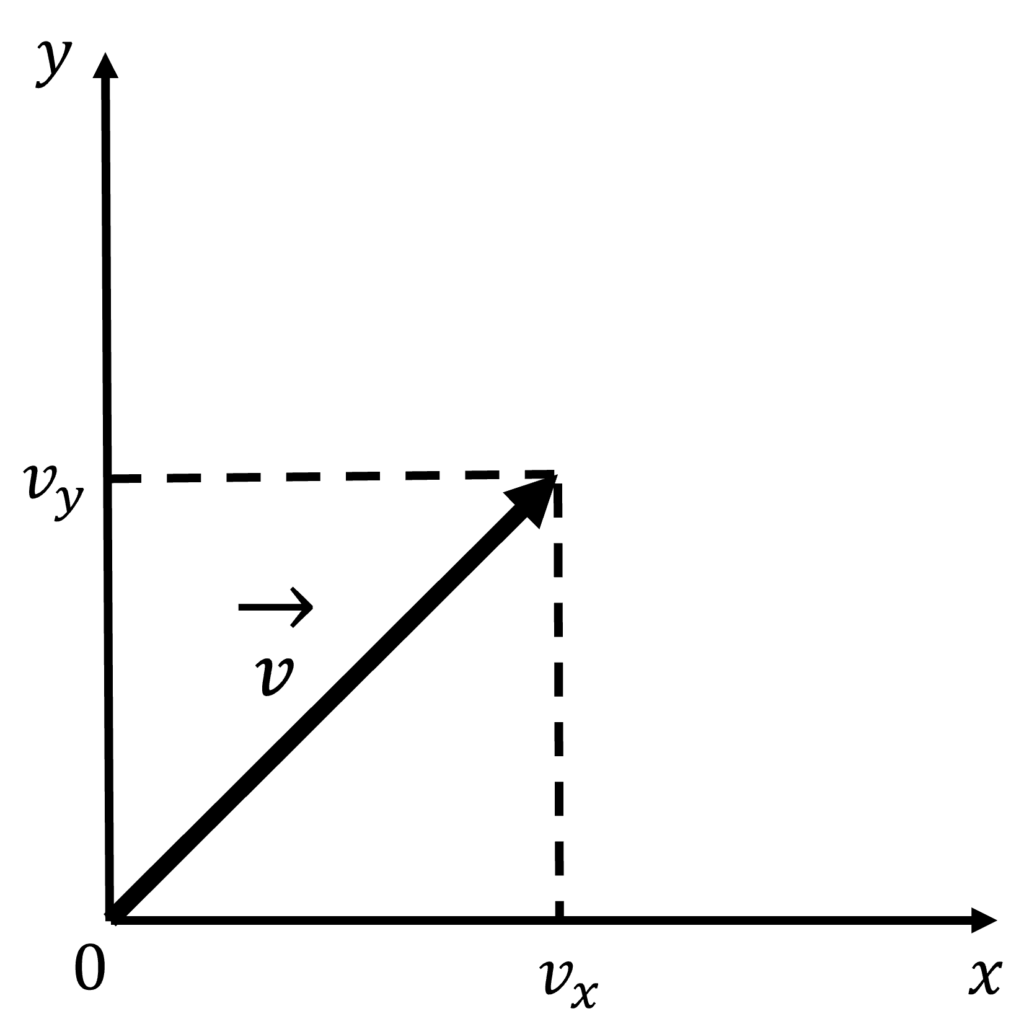
速度ベクトル
$$\vec{v} = (v_x, v_y)$$
単位時間(1秒間)に,x軸方向に距離\(v_x\),y軸方向には距離\(v_y\)進むような,向きと長さを示す矢印.
2. ベクトルを任意の角度だけ回転させる
\(\vec{v} = (v_x, v_y)\)を,角度\(\theta\)回転させてみましょう.ここで,回転後のベクトルを\(\vec{w}\)とします(下図).この時,\(\vec{w}=(w_x, w_y)\)は,元々のベクトルの各要素\(v_x, v_y\)と回転角度\(\theta\)を用いて,どのように表せるでしょうか?
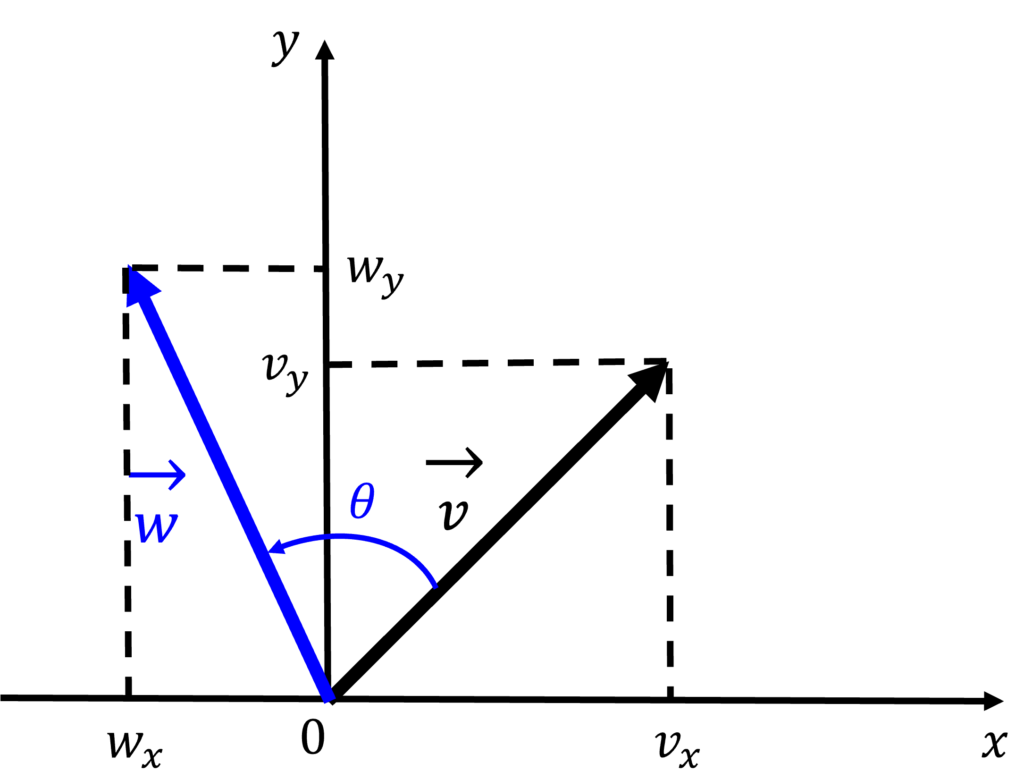
ベクトルをある角度だけ回転させるには,「回転行列\(R(\theta)\)」を,回転させたいベクトルにかける方法が便利です.行列と聞くと,「線形代数なんて忘れちゃったよ」という方も多いでしょう.しかし,「行列の掛け算」さえ復習すれば問題ありません.
ここで,ベクトルの表し方は,次の2通りあります.
\begin{align*}
\vec{v} = (v_x, v_y)\\
\vec{v} =
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}
\end{align*}
どちらにしても,ベクトルの要素(x成分,y成分)を左から右に向かって横に並べても,上から下の順で並べても同じベクトルを意味します.前者は文章の中に入れて書きやすいメリットがありますが,今回のように,行列をかけるときは後者が便利です.
そして,ベクトルを回転させる計算方法は,次のようになります.
ベクトル\(\vec{v} = (v_x, v_y)\)を,角度\(\theta\)だけ回転させる.
\begin{align*}
\vec{w} &= R(\theta)\vec{v} \\
&= \begin{pmatrix}
\mathrm{cos}\theta & -\mathrm{sin}\theta \\
\mathrm{sin}\theta & \mathrm{cos}\theta
\end{pmatrix}
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}\\
&= \begin{pmatrix}
v_x\mathrm{cos}\theta -v_y\mathrm{sin}\theta \\
v_x\mathrm{sin}\theta + v_y\mathrm{cos}\theta
\end{pmatrix}
\end{align*}
3. 注目するベクトルと同じ向き(進行方向)の単位ベクトル
\(\vec{v}\)と同じ向きをもつベクトルを求める場合,\(\theta = 0^{ \circ }\)であるため,回転行列をかけても,ベクトルは変化しません.よって,今は,回転行列をかける必要は無いです.
そして,所望の単位ベクトルは,\(\vec{v} = (v_x, v_y)\)の各成分を,ベクトルの大きさ\(|\vec{v}| = \sqrt{v_x^2 + v_y^2})\)で割ることで求まります.ベクトルを定数倍するとき,大きさは定数倍されるものの,その向きは変わりません.そして,長さ1,\(\vec{v}\)と同じ向きを持ったベクトル\(\vec{s}\)は,次式のように得られます.
\begin{align*}
\vec{s} &= \frac{\vec{v}}{|\vec{v}|}\\
&= \frac{1}{\sqrt{v_x^2 + v_y^2}}\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}
\end{align*}

ベクトル\(\vec{s}\)の大きさ\(|\vec{s}| = \sqrt{s_x^2 + s_y^2}\)を計算すると,1になることは,容易に確認することができます.
4. 注目するベクトルに直行する向きの単位ベクトル
一般に,回転角度は,左回転(反時計回り)を正とします.よって,本記事でも,回転角度の正の方向は反時計回りの向きとします.
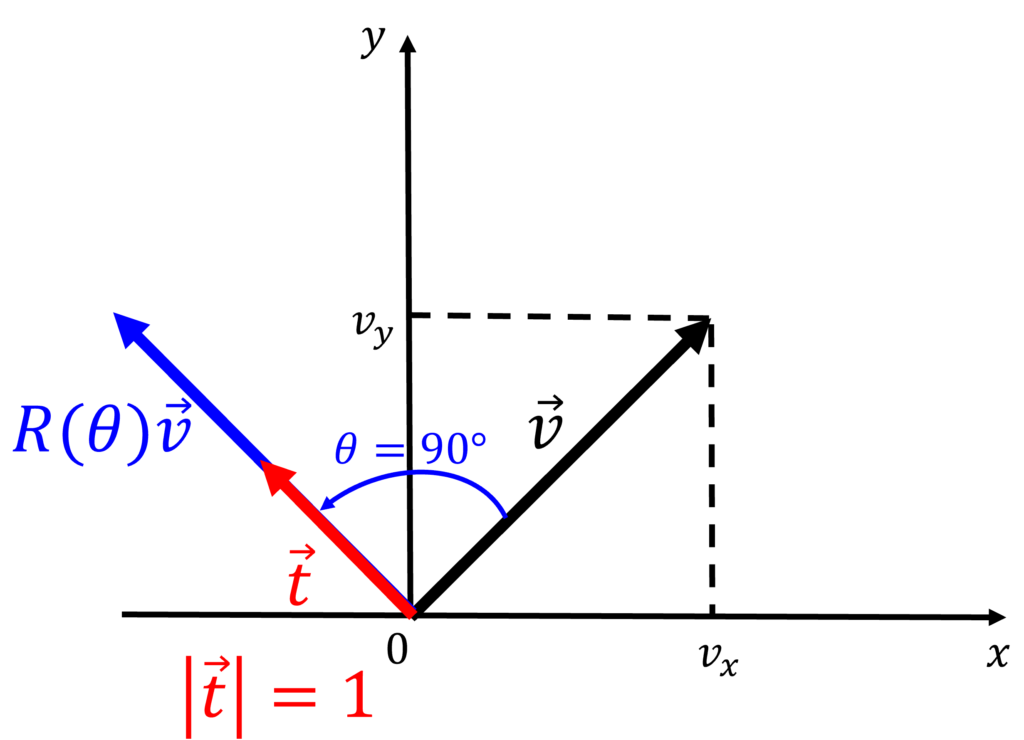
左に90度回転させるときは,\(\theta = 90^{ \circ }\)とします.すなわち,\(\vec{v}\)の方向を向いたとき,左に90度回転した方向で,長さ1を持つ単位ベクトルは,次式のように求めることができます.
\begin{align*}
\vec{t} & = R(90^{ \circ })
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}\frac{1}{\sqrt{v_x^2 + v_y^2}}\\
&= \frac{1}{\sqrt{v_x^2 + v_y^2}}
\begin{pmatrix}
0 & -1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}\\
&= \frac{1}{\sqrt{v_x^2 + v_y^2}}
\begin{pmatrix}
-v_y \\
v_x
\end{pmatrix}
\end{align*}
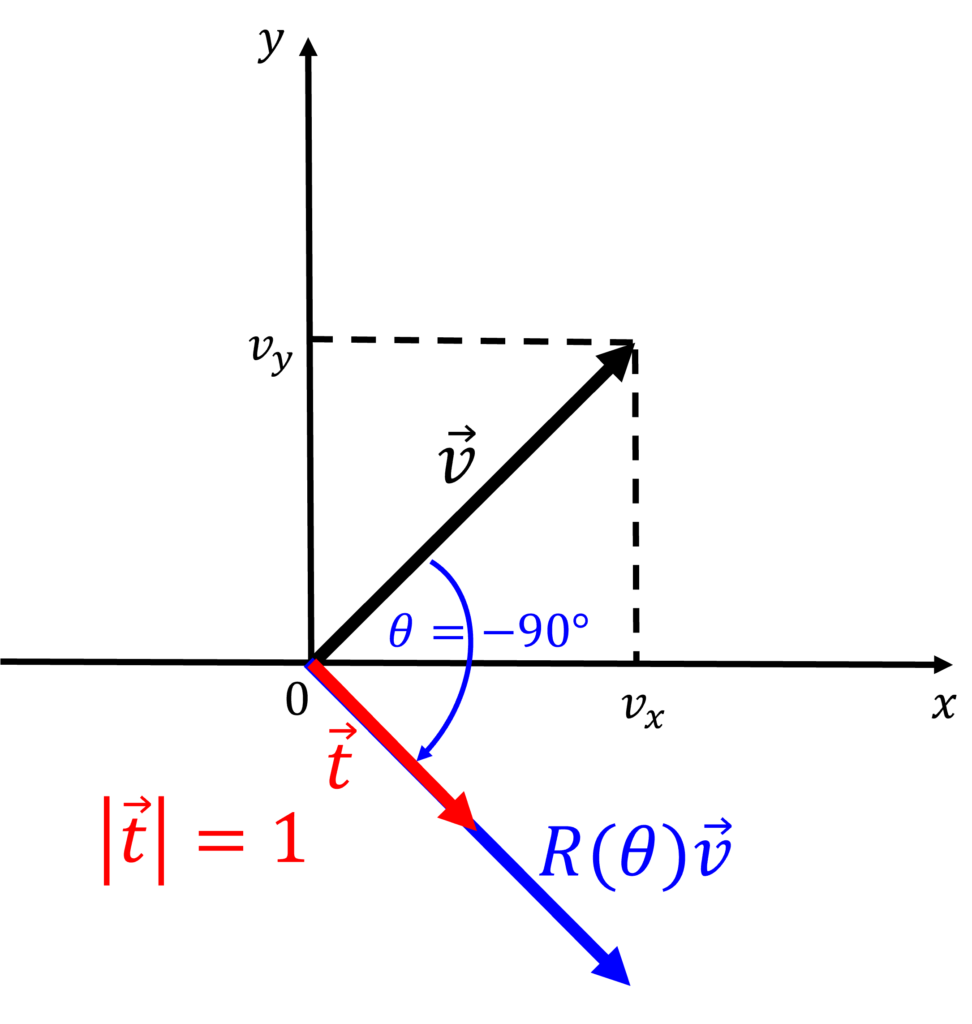
右に90度回転させたいときは,\(\theta = -90^{ \circ }\)とします.すなわち,\(\vec{v}\)の方向を向いたとき,右に90度回転した方向で,長さ1を持つ単位ベクトルは,次式のように求めることができます.
\begin{align*}
\vec{t’} &= R( – 90^{ \circ })
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}\frac{1}{\sqrt{v_x^2 + v_y^2}}\\
&=\frac{1}{\sqrt{v_x^2 + v_y^2}}
\begin{pmatrix}
0 & 1 \\
-1 & 0
\end{pmatrix}
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}\\
&= \frac{1}{\sqrt{v_x^2 + v_y^2}}
\begin{pmatrix}
v_y \\
-v_x
\end{pmatrix}
\end{align*}
さいごに
本記事では,回転行列を用いて,ベクトルに対してある角度だけ回転した方向を持ったベクトルを求める方法を解説してきました.回転行列やベクトルに慣れない方も多いと思います.しかし,ベクトルに具体的な値を入れてみたり,角度に値を代入したりして,実際に計算してみると,理解が直感的なものになっていくでしょう.
雑談
移動体(車や飛行機,衛星等)や,走っている人間の移動速度を矢印で表すのは,非常に直感的です.長い矢印を描けば「速く」移動している様子を表現できますし,矢印の向きで,「移動方向」も表現できます.そして,数学的にも,速度とは,大きさと向きを持った「ベクトル」です.ここで,「ベクトル」は,英語ではVectorです.また,「速度」は英語でVelocityです.このような事情から,ベクトルを\(\vec{v}\)という記号で表すことは,VectorやVelocityという単語と親和性が高いので,直感的な理解を助けてくれるなあと思います.



コメント