今回は、私が学部・大学院での研究データの解析でよく用いていた
Pythonを用いた
カーブフィッティング(曲線近似)と、それによるパラメータの最適化手法を解説します。
分野によって用いる近似曲線は異なると思いますが、
- 直線近似
- ガウス分布に近似する
この2つは多くの分野で出会うのではないでしょうか。例えば化学系の実験では、吸光係数を決定するために直線近似を用いますが、これはExcelでできてしまいます。しかし、
- 非線形の複雑な関数でのフィッティング
- フィッティングした後の、パラメータの誤差(標準誤差)を求める
となると、グラフソフトなどを用いないと難しいと思います。
そこで、
パラメータの初期値を適当に設定しさえすれば、
任意の関数・複数のパラメータが含まれている関数に対して、曲線近似ができ、パラメータのフィッティング誤差まで求めることができる手法
を紹介します。
なお、本記事では1変数関数のフィッティングについて解説していますが、多変数関数のフィッティングを行うことも可能です。↓の記事では、変数x, yの2変数に依存する2次元ガウス関数のフィッティングを例に、多変数関数の場合について解説しています。
1. 使用するライブラリと関数の準備
Scipyのcurve_fit関数が、本記事で最も重要な役割を果たしています。
<curve_fitの基本的な使い方>
curve_fit(近似したい関数, x軸のデータ, y軸のデータ, 関数のパラメータの初期値)
また、今回は代表として5つの関数を用意してみました。
# ライブラリのインポート
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np
# モデル関数の定義
def proportion(x, a):
"""原点を通る直線"""
return a * x
def line(x, a, b):
"""原点を通らない直線"""
return a * x + b
def tanh(x ,a , b):
"""増加量が頭打ちになる関数"""
return a * np.tanh(b * x)
def parabola(x, a):
"""二次関数(放物線)"""
return a * x**2
def gauss_func(x,a,mu,sigma):
"""ガウシアン(正規分布)"""
return a*np.exp(-(x-mu)**2/(2*sigma**2))2. データの用意
次に、曲線近似したいデータを用意します。研究や実験でいうと、
これが何らかの測定値の生データに相当します。
上記の5つの関数のそれぞれに対応したデータを用意します。
# データの用意
data_proportion = np.array([
[1, 2, 3, 4, 5],
[2, 4.2, 5.3, 8, 10.1],
])
data_line = np.array([
[0, 1, 2, 3, 4, 5],
[2, 4, 6.2, 7.3, 10, 12.1],
])
data_tanh = np.array([
[1, 2, 3, 4, 5],
[1, 2, 2.5, 3, 3],
])
data_parabola = np.array([
[1, 2, 3, 4, 5],
[1, 4.1, 8.8, 15, 24.6],
])
data_gauss_func = np.array([
[0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5],
[0, 0.5, 2.5, 4.5, 6, 7, 6.5, 4.5, 2.4, 0.5, 0],
])3. パラメータの初期値を設定
次に、パラメータの初期値を設定します。適当な値でいいのですが、それっぽい値を設定することが、
正確にフィッティングするポイントです。
例えば、原点を通る直線に近似させるために用意したデータdata_proportionを見ると、大体傾きが2になりそうなことが分かります。つまり、パラメータ a (傾き)の初期値として、2に近い値を設定しておくのが吉です。
もう一つ例を挙げます。原点を通らない直線に近似させるために用意したデータdata_lineを見ると、大体傾きが2、切片が2になりそうなことが分かります。つまり、パラメータ a, b (傾き, 切片)の初期値として、[2, 2]のような値を設定しておくとよいのです。
※ここで、パラメータの初期値はあくまで「初期値」です。
よって、最初の例でいえば、a の初期値は2.1でも1.7でも(おそらく1くらいでも)、curve_fitによって最適化されれば、a≒2となり、最終的には同じ値が求まります。
# パラメータの初期値の設定
param_init_dict = {
"proportion":[2],
"line":[2, 2],
"tanh":[3, 0.6],
"parabola":[1],
"gauss_func":[7, 2.5, 1]
}
# グラフ描画用のサンプルデータ
sample_x = np.arange(0, 5, 0.01)4. カーブフィッティングを実行
いよいよ、フィッティングを行います。
ここで注意したいのは、curve_fit関数を実行すると、結果としてpopt, pocvが出力される点です。
poptは各パラメータの最適化推定値であり、pocvはパラメータの分散共分散行列です。
perr = np.sqrt(np.diag(pocv))によってpocvの対角成分を抽出し、np.sqrtで平方根をとれば各パラメータの標準誤差が求まります。
(例)gauss_funcに近似させた場合
popt = [7.18073987, 2.51385529, 0.98171401] (= [a, mu, sigma])
peer = [0.21115349, 0.03331323, 0.03343835] (= [Δa, Δmu, Δsigma])
つまりは、
a = 7.18 ± 0.21, mu = 2.51 ± 0.03, sigma = 0.98 ± 0.03
がフィッティングの結果となります。
# フィッティングを行うための関数
def fit(func, x, param_init):
"""
func:データxに近似したい任意の関数
x:データ
param_init:パラメータの初期値
popt:最適化されたパラメータ
pocv:パラメータの共分散
"""
X = x[0]
Y = x[1]
popt,pocv=curve_fit(func, X, Y, p0=param_init)
perr = np.sqrt(np.diag(pocv)) #対角成分が各パラメータの標準誤差に相当
y=func(sample_x, *popt)
return y, popt, perr5. フィッティングの実行結果を可視化する
result = fit(proportion, data_proportion, param_init_dict["proportion"])
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(data_proportion[0], data_proportion[1])
ax.plot(sample_x, result[0])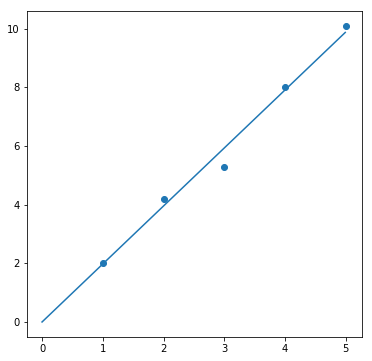
result = fit(line, data_line, param_init_dict["line"])
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(data_line[0], data_line[1])
ax.plot(sample_x, result[0]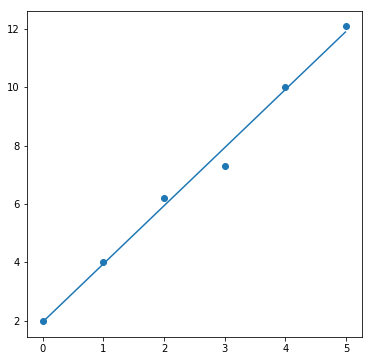
result = fit(tanh, data_tanh, param_init_dict["tanh"])
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(data_tanh[0], data_tanh[1])
ax.plot(sample_x, result[0])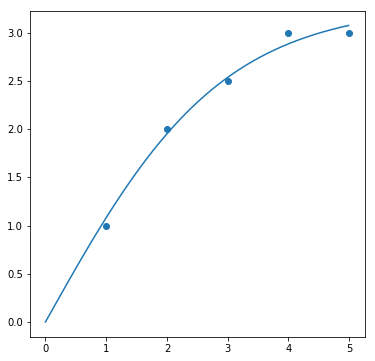
result = fit(parabola, data_parabola, param_init_dict["parabola"])
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(data_parabola[0], data_parabola[1])
ax.plot(sample_x, result[0])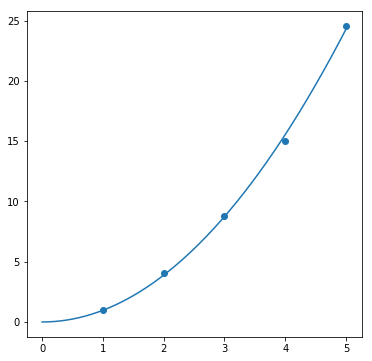
result = fit(gauss_func, data_gauss_func, param_init_dict["gauss_func"])
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(data_gauss_func[0], data_gauss_func[1])
ax.plot(sample_x, result[0])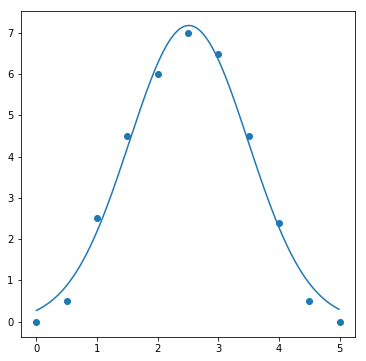
また、ガウス関数によるフィッティング(ガウスフィッティング)は、統計的にデータを解析する際に極めて重要です.詳しくは、以下の記事で解説しています.
さいごに
今回は、Pythonを用いたカーブフィッティングの手法を紹介してきました。
適切なパラメータの初期値さえ与えれば、任意の関数に対応できる方法なので、
三角関数や指数関数、3次関数、4次関数…と様々な使い道があります。
今後も使用する機会がありそうです。
なお、本記事では1変数関数でのフィッティングを解説しましたが、多変数関数の場合(ガウス関数のフィッティング)については次の記事で紹介しております。


コメント