【多変数関数】Scipyのcurve_fitで２次元ガウスフィッティング（Python）

１変数関数の曲線近似（カーブフィッティング）についてはこちらの記事で解説しています。１次元ガウスフィッティングの方法も紹介しております。

【曲線近似】Scipyのcurve_fitを用いて、任意の関数でカーブフィッティング（Python）

大学の研究などで、取得したデータを直線近似したり、非線形関数やガウス関数といった複雑な関数で近似する必要のある場面は多いと思います。そこで、機械学習ライブラリを使って、簡単に、しかも任意の関数に対してカーブフィッティング（曲線近似）を行い、パラメータの誤差まで算出できる便利な方法を紹介したいと思います。

１次元ガウス関数の復習

$$f(x) = A\mathrm{exp}\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$$

変数は$x$、パラメータはピーク値$A$、中央値$\mu$、標準偏差$\sigma$の３つとなります。確率密度関数は$A=\frac{1}{\sqrt{2\pi}\sigma}$の場合に相当します。確率密度関数では、$A$は全領域での積分値が１になるように規格化してあります。

２次元ガウス関数と具体例

天体（星）の画像データを例に

光の強度は、天体の中心をピークに、球状に分布します。天体と言われてもピンと来ない方もいらっしゃるでしょう。電球や、夜に前から向かってくる車のヘッドライトをイメージしてもらえばわかりやすいかと思います。その光の強度分布を、２次元平面に落とし込んだのが天体画像（カメラで撮った電球の写真）です。２次元画像において、光の強度は、星の中心をピークに、おおよそガウス関数の形で広がりを持ちます。

細かい話
※天体は３次元的な物体ですから、球の中心から放射状に光を発し、その強度は中心からの距離の２乗に反比例します。また、天文学の研究においては、コンティニューム（連続光）といって、観測されたすべての周波数領域の光の強度（フラックス）を足し合わせたデータにガウスフィッティングを適用して、天体の中心を推定することがよくあります。

さて、上のような画像データが与えられ、星の中心を厳密に推定したいとします。光の強度分布はおおよそガウス分布に従うことを仮定すれば、星の中心は、光の強度分布を２次元ガウス関数でフィッティングし、ガウス関数のピークを与える座標に存在すると考えられます。

光の強度は、x, y方向それぞれについて、ガウス分布に近い形で広がっていると考えらます。すなわち、各方向への広がり方は、次のように表すことができます。

$$f(x) = A_x\mathrm{exp}\left(-\frac{(x-\mu_x)^2}{2\sigma_x^2}\right)$$

$$f(y) = A_y\mathrm{exp}\left(-\frac{(x-\mu_y)^2}{2\sigma_y^2}\right)$$

X, Yが独立な変数であれば、上の２つを掛け合わせて、２次元ガウス関数を次のように表すことができます。

\begin{align*}
f(x, y) &= f(x)f(y)\\
&= A\mathrm{exp}\left(-\frac{(x-\mu_x)^2}{2\sigma_x^2}\right)\mathrm{exp}\left(-\frac{(x-\mu_y)^2}{2\sigma_y^2}\right)
\end{align*}

ここで、光の強度分布画像では、ピーク（最も明るい場所）の値が$A$に相当します。

Pythonにおけるガウス関数の実装は次のようになります。

def gauss_2d(X , A, sigma_x, sigma_y, mu_x, mu_y):
    x, y = X
    z = A * np.exp(-(x-mu_x)**2/(2*sigma_x**2)) * np.exp(-(y-mu_y)**2/(2*sigma_y**2))
    return z

カーブフィッティングを実行

今回の記事で、最も注目すべき点は機械学習ライブラリScipyのcurve_fit関数を使えば、私たちの持っているデータを、あらゆる関数でフィッティングできるということです。基本的には、次のことを押さえておけばOKです。

<curve_fitの基本的な使い方>
curve_fit(近似したい関数, x軸のデータ, y軸のデータ, 関数のパラメータの初期値)

今回は２変数関数を用いているため、議論がやや複雑になっています。イメージしにくい場合は、こちらの記事で紹介する１変数関数への適用例を先にご覧いただくことをお勧めします。

【曲線近似】Scipyのcurve_fitを用いて、任意の関数でカーブフィッティング（Python）

では、一気にフィッティングを行っていきます。

import numpy as np
from scipy.optimize import curve_fit
from matplotlib import pyplot as plt

def gauss_2d(X , A, sigma_x, sigma_y, mu_x, mu_y):
    x, y = X
    z = A * np.exp(-(x-mu_x)**2/(2*sigma_x**2)) * np.exp(-(y-mu_y)**2/(2*sigma_y**2))
    return z.ravel()
# データを生成
x_data, y_data = np.meshgrid(np.linspace(-5, 5, 100), np.linspace(-5, 5, 100))
z_data = gauss_2d((x_data, y_data), 8, 2.0, 2.0, 1.0, -1.5)
# データを現実っぽくするために、ばらつきを持たせた
observed_data = z_data + np.random.normal(scale=0.2, size=z_data.shape)

#param_init = [8, 2, 2, 1, -1.5]
X = np.array([x_data, y_data])
popt, pcov = curve_fit(gauss_2d, X, observed_data) #param_initを指定することもできる
perr = np.sqrt(np.diag(pcov)) 
# 求まった最適値
A, sigma_x, sigma_y, mu_x, mu_y = popt

fig, ax = plt.subplots(1 , 2, figsize=(16, 6))
# Left figure
im = ax[0].pcolormesh(x_data, y_data, observed_data.reshape(x_data.shape), cmap="plasma")
fig.colorbar(im, ax=ax)

# Right figure
theta = np.linspace(0, 2*np.pi, 100)
a = sigma_x*np.cos(theta) + mu_x
b = sigma_y*np.sin(theta) + mu_y
ax[1].pcolormesh(x_data, y_data, observed_data.reshape(x_data.shape), cmap="plasma")
ax[1].plot(a, b)
ax[1].set_aspect(1)
ax[1].plot(mu_x, mu_y, marker="*", ms=20, color="black")

フィッティングの結果、推定されたパラメータ(poptに格納される)は次のようになります。また、各パラメータの推定誤差はperrに格納されます。

print(popt)
>> [ 7.99919598,  1.99897742,  2.00251662,  1.00072304, -1.49963915]
# それぞれA, sigma_x, sigma_y, mu_x, mu_yに対応

フィッティング結果を図示します。左側の図には、$(\mu_x, \mu_y)$を中心（黒い星）とし、長軸（短軸）の長さを$\sigma_x, \sigma_y$とする楕円を描きました。すなわち、観測された光の強度の総量の内、約68%は円の内側の領域に存在することを意味しています。

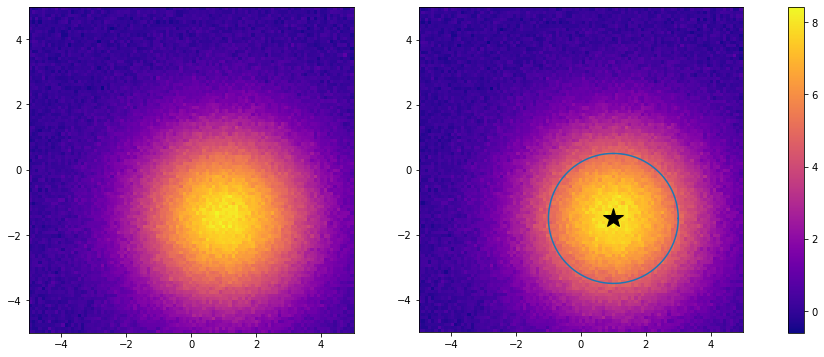
これで、星の光の強度分布から、星の中心を推定することができました！

注意点と躓きポイント

多変数関数の扱に関する注意点

curve_fitにおいて、説明変数は多変数、多次元でもよいですが、１つの変数Xとしてまとめて入力あるいは(x, y)としないといけないらしい。また、機械学習ライブラリであるが、基本的には予測値$\hat{z}$と$z$の差によってパラメータの推定値を評価することになるため、関数の出力結果$z$と予測値$\hat{z}$はベクトルの形式でなければいけません。よって、

def gauss_2d(X , A, sigma_x, sigma_y, mu_x, mu_y):
    x, y = X
    z = A * np.exp(-(x-mu_x)**2/(2*sigma_x**2)) * np.exp(-(y-mu_y)**2/(2*sigma_y**2))
    return z

のようにzを出力した場合、x, yが多次元になるので、zも多次元となる。すると、次のようなエラーが返されてしまいます。

Result from function call is not a proper array of floats.

これを避けるため、出力は１次元配列としましょう。

def gauss_2d(X , A, sigma_x, sigma_y, mu_x, mu_y):
    x, y = X
    z = A * np.exp(-(x-mu_x)**2/(2*sigma_x**2)) * np.exp(-(y-mu_y)**2/(2*sigma_y**2))
    return z.ravel()