前回の記事
で比熱の表式を求めるのに用いた「アインシュタインモデル」の問題点を解決するべく、本記事では、デバイモデルにおける3次元結晶の比熱を調べていく。
1. 準備:調和振動子のエネルギーの期待値を求める
調和振動子のエネルギー固有値は
$$E_n = \left(n+\frac{1}{2}\right)\hbar\omega \ (n=0, 1, 2…)$$
しかし、これはミクロな系でのエネルギー固有値を表しているため、統計力学の対象にすることができない。よって、カノニカル分布を適用し、エネルギーの期待値を求めておく必要がある。
分配関数は
\begin{align*}
Z &= \sum_{n_i=0}^{\infty}e^{-\beta\hbar\omega\left(n_i+\frac{1}{2}\right)}\\
&= e^{-\frac{\beta\hbar\omega}{2}}\sum_{n_i=0}^{\infty}\left(e^{-\beta\hbar\omega}\right)^{n_i}\\
&= e^{-\frac{\beta\hbar\omega}{2}}\cdot\frac{1}{1-e^{-\beta\hbar\omega}}\\
&= \left(2sinh\frac{\beta\hbar\omega}{2}\right)^{-1}
\end{align*}
エネルギー固有値の期待値は
\begin{align*}
\langle \hat{H} \rangle &= -\frac{\partial}{\partial \beta}lnZ\\
&= \frac{\hbar\omega}{2}tanh^{-1}\frac{\beta\hbar\omega}{2}\\
&= \frac{\hbar\omega}{2} + \frac{\hbar\omega}{e^{\beta\hbar\omega}-1}
\end{align*}
ここで
\begin{align*}
tanh^{-1}x &= \frac{coshx}{sinhx}\\
&= \frac{e^x+e^{-x}}{e^x-e^{-x}}\\
&= \frac{(e^x-e^{-x})+2e^{-x}}{e^x-e^{-x}}\\
&= 1 + \frac{2}{e^{2x}-1}
\end{align*}
であることを用いた。
さて、ここまで
- 調和振動子の分配関数を求める。
- 分配関数をもとに調和振動子のエネルギーの期待値を求める。
アインシュタインモデルと全く同じ議論である。
2-1. 調和振動子の”集合”としての連成振動を考える(1次元系)
まず、1次元の
各粒子の安定な配置は、各格子点の座標であるから
$$\chi = {a, 2a, … Na}$$
である。この時、粒子\(i\)の安定な配置からのズレを\(q_i\)とすると、全粒子のハミルトニアンは次のように表される。
$$H(q_a, q_{2a}, … q_{Na}) = \sum_{x \in \chi}\frac{p_x^2}{2m} + \frac{\kappa}{2}\sum_{x=0, a, … Na}(q_{x+a}-q_x)^2$$
ここで、\(q_0 = q_{(N+1)a} = 0\) である。粒子の安定点からのズレは、1つ右の粒子の安定点からのズレを含む。よって、\(q_{x+a}-q_x)で1つ右の粒子からの寄与を差し引くことで、正確なポテンシャルを表現することができる。
さて、今考えている系において粒子の運動は周囲の他の粒子の伝播するため、各粒子の振動は独立ではない。しかし、各粒子の振動を、安定な配置からの位置のズレではなく、
$$k = \frac{\pi}{(N+1)a}, \frac{2\pi}{(N+1)a}, … \frac{N\pi}{(N+1)a}$$
の値をとる波数で指定することで、N個の独立な調和振動子とみなすことができる。そして、波数\(k\)に対応する振動子の角振動数は次のように表される。
$$\omega (k) = 2\sqrt{\frac{\kappa}{m}}sin\frac{ak}{2}$$
\(k, \omega (k)\)の導出には、運動方程式の解を固有振動の重ね合わせで書けることを示したうえで、フーリエ展開を用いて、調和振動子とみなせる各固有振動に対応した固有値、固有振動数を具体的に計算する必要がある。しかし、本記事ではそこには触れていない。
ニュートン力学における連成振動の固有振動への分解、そして解析力学・量子力学における同様の議論は複雑なので、今回はそれらから得られる結果を天下り的に利用した。振動・波動分野も含め、本格的に勉強してみたい。
2-2. 調和振動子の”集合”としての連成振動を考える(3次元系)
3次元の連成振動モデルでは、縦・横・奥行方向にL個ずつ粒子が並んでいる状況を考える。
1つの粒子の安定な配置は
$$\mathbf{r} = (an_1, an_2, an_3)$$
で表すことができる。よって、\(N = L^3\)の各粒子の安定な配置の集合
$$\Lambda = {(an_1, an_2, an_3) | n_1, n_2, n_3 = 1, 2, … L}$$
系全体のハミルトニアンは
$$H= \sum_{\mathbf{r} \in \Lambda}\frac{\mathbf{p}_{\mathbf{r}}^2}{2m} + \frac{\kappa}{2}\sum_{\mathbf{r} \in \Lambda}\sum_{\nu = 1}^3\sum_{\nu ‘ = 1}^3(q_{\mathbf{r}+a\mathbf{e}(\nu ‘)}^{(\nu)}-q_{\mathbf{r}}^{(\nu)})^2$$
固有振動を指定する波数ベクトル\(\mathbf{k} = (k_x, k_y, k_z)\)は、
$$K = {\left(\frac{m_x\pi}{(N+1)a}, \frac{m_y\pi}{(N+1)a}, \frac{m_z\pi}{(N+1)a}\right)|n_x, m_y, m_z = 1, 2, … L}$$
という集合の要素で指定される。そして、各\(\mathbf{k}\)に、振動数
$$\omega (\mathbf{k}) = 2\sqrt{\frac{\kappa}{m}}\sqrt{\sum_{\nu = 1}^3\left(sin\frac{ak_{\nu}}{2}\right)^2}$$
を持つ調和振動子が対応する。x, y, zの3つの成分が含まれることを表している。
では、系のエネルギーの期待値を求める。N個の粒子の振動を\(3N = 3L^3\)個の調和振動子の重ね合わせで表すことができると分かったので、系全体のエネルギーの期待値は、各調和振動子のエネルギーの期待値の和で表される。すなわち
$$\langle \hat{H} \rangle = 3\sum_{\mathbf{k} \in K}\left\{\frac{\hbar\omega (\mathbf{k})}{2} + \frac{\hbar\omega (\mathbf{k})}{e^{\beta\hbar\omega (\mathbf{k})}-1}\right\}$$
3. 高温での比熱の振る舞い
\(\omega\)の最大値は、
$$\omega_{max} = 2\sqrt{\frac{3\kappa}{m}}$$
であることから、十分高温(\(\beta\hbar\omega_{max} << 1\))のときのエネルギーの期待値は
$$\langle \hat{H} \rangle \cong 3Nk_BT = 3nRT$$
よって、熱容量は
$$\frac{\partial \hat{H}}{\partial T} = 3nR$$
となり、デュロン・プティの法則を満たす。
他の温度帯での比熱の振る舞いを調べるための準備
まず、途中計算をシンプルにするために、温度に依存しない(\(beta\) を含まない)部分を1つの定数にまとめる。
$$E_0 = \sum_{\mathbf{k} \in K}\frac{\hbar\omega (\mathbf{k})}{2}$$
$$\langle \hat{H} \rangle = E_0 + 3\sum_{\mathbf{k} \in K}\frac{\hbar\omega (\mathbf{k})}{e^{\beta\hbar\omega (\mathbf{k})}-1}$$
ここで、和\(\sum_{\mathbf{k} \in K}\)を\(\mathbf{k}\)の積分(\(k_x, k_y, k_z\))の三重積分)に直す。
\begin{align*}
\langle \hat{H} \rangle &= E_0 + 3\left(\frac{(L+1)a}{\pi}\right)^3\sum_{\mathbf{k} \in K}\left(\frac{\pi}{(L+1)a}\right)^3\frac{\hbar\omega (\mathbf{k})}{e^{\beta\hbar\omega (\mathbf{k})}-1}\\
& \cong E_0 + 3\left(\frac{(L+1)a}{\pi}\right)^3\int_0^{\pi /a}\int_0^{\pi /a}\int_0^{\pi /a}dk_xdk_ydk_y\frac{\hbar\omega (\mathbf{k})}{e^{\beta\hbar\omega (\mathbf{k})}-1}
\end{align*}
【\(\mathbf{k}\)の和を積分に直すには】
$$\mathbf{k} = \left(\frac{m_x\pi}{(N+1)a}, \frac{m_y\pi}{(N+1)a}, \frac{m_z\pi}{(N+1)a}\right)$$
$$dk = \frac{\pi}{(L+1)a}dm = \frac{\pi}{(L+1)a} = \Delta$$
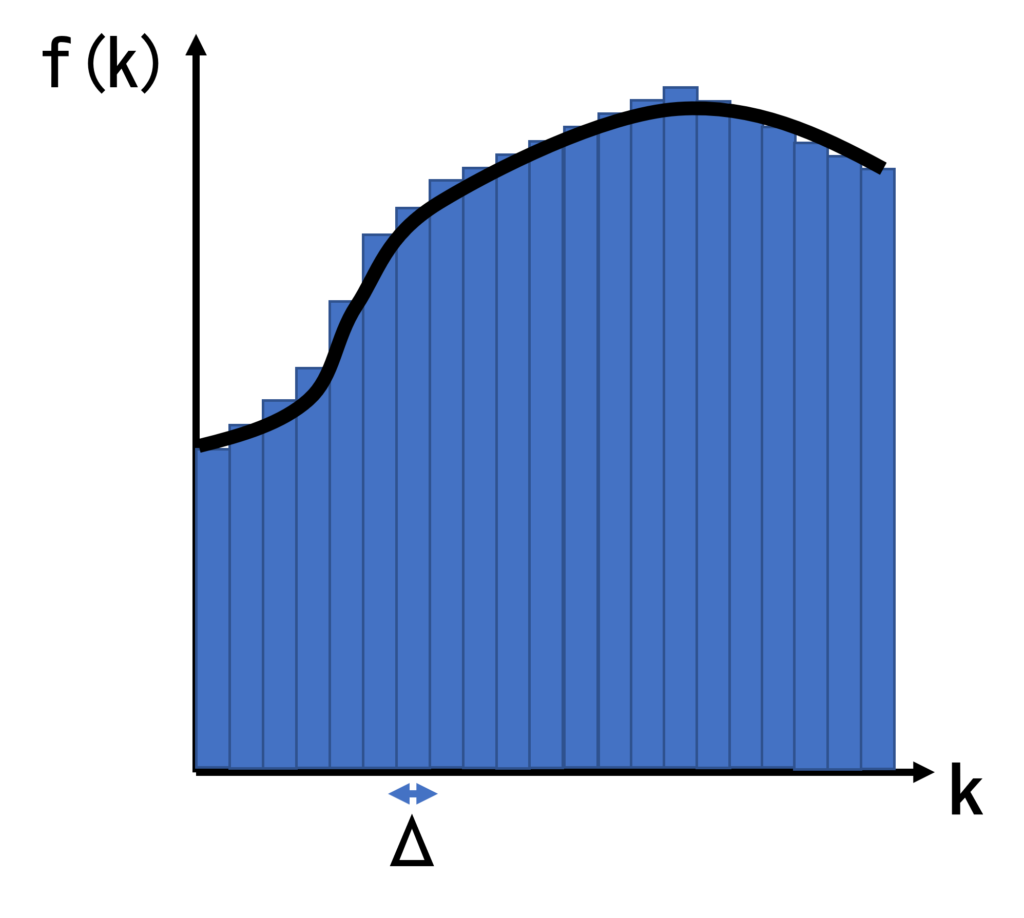
図のように、\(k\)の関数\(f(k)\)があるとき、\(\sum_k f(k)\Delta\)は短冊の面積を足し上げることに相当する。もし、\(f(k)\)の変化高に対して\(\Delta\)が十分に小さければ、次式のように和を積分に直すことができる。
$$\sum_k f(k)\Delta = \int f(k)dk$$
よって、
$$\sum_k f(k) = \frac{1}{\Delta}\sum_k f(k)\Delta \cong \frac{1}{\Delta}\int f(k)dk$$
モル比熱は、\(\varepsilon_0 = \frac{E_0}{n}\)を持ちいて
\begin{align*}
\frac{\langle \hat{H} \rangle}{n}&= \varepsilon_0 + \frac{3V_0}{\pi^3}\int_0^{\pi /a}\int_0^{\pi /a}\int_0^{\pi /a}dk_xdk_ydk_z\frac{\hbar\omega (\mathbf{k})}{e^{\beta\hbar\omega (\mathbf{k})}-1}\\
&= \varepsilon_0 + \frac{3V_0}{(2\pi)^3}\int_{-\pi /a}^{\pi /a}\int_{-\pi /a}^{\pi /a}\int_{-\pi /a}^{\pi /a}dk_xdk_ydk_z\frac{\hbar\omega (\mathbf{k})}{e^{\beta\hbar\omega (\mathbf{k})}-1}
\end{align*}
2行目では、各方向につき、積分区間を2倍にし、その分全体を2で割った。
\begin{align*}
C(T) &= \frac{d}{dT}\left(\frac{\langle \hat{H} \rangle}{n}\right)\\
&= \frac{3V_0}{(2\pi)^3}\int_{-\pi /a}^{\pi /a}\int_{-\pi /a}^{\pi /a}\int_{-\pi /a}^{\pi /a}dk_xdk_ydk_z\frac{(\hbar\omega (\mathbf{k}))^2}{k_BT^2}\left\{2sinh\frac{\hbar\omega (\mathbf{k})}{2k_BT}\right\}^{-2}
\end{align*}
\(\mathbf{k}\)の積分の被積分関数は複雑であるため、正確に計算することはできない。よって、低温での比熱を解析的に評価するためには、近似を用いる必要がある。
4. 低温での比熱の振る舞い
十分低温(\(\beta\hbar\omega_{max} << 1\))の場合を考える。
\(\frac{\langle \hat{H} \rangle}{n}\)の被積分関数は、\(\beta\hbar\omega(\mathbf{k})\)が極めて大きいとき、分母は極めて大きくなる。よって、十分低温の領域では、0に近い値をとるため積分への寄与が極めて小さくなる。一方、この効果を打ち消しうる要素は\(\omega(\mathbf{k})\)の大きさである。\(\omega(\mathbf{k})\)が極めて小さければ、被積分関数は一定の大きさを持つことができる。これを上手く使えば、積分を近似によって単純化できる。ここで
$$\omega (\mathbf{k}) = 2\sqrt{\frac{\kappa}{m}}\sqrt{\sum_{\nu = 1}^3\left(sin\frac{ak_{\nu}}{2}\right)^2}$$
この表式を見ると、\(\omega(\mathbf{k})\)が極めて小さくなるためには、sin関数が極めて0に近い必要がある。すなわち、\(a|\mathbf{k}| \cong 0\)であればよい。
まとめると、十分低温(\(\beta\hbar\omega_{max} << 1\))の場合、積分に寄与する\(\mathbf{k}\)は、\(a|\mathbf{k}| \cong 0\)を満たす領域だけである。
したがって、\(sin\theta \cong \theta \ (\theta << 1)\)を用いて
\begin{align*}
\omega (\mathbf{k}) &\cong 2\sqrt{\frac{\kappa}{m}}\sqrt{\sum_{\nu = 1}^3\left(\frac{ak_{\nu}}{2}\right)^2}\\
&= \sqrt{\frac{\kappa}{m}}a|\mathbf{k}|\\
&= v_0|\mathbf{k}|
\end{align*}
ここで、結晶中の音速\(v_0 = \sqrt{\frac{\kappa}{m}}a\)を用いた。
前述したように、積分には、\(a|\mathbf{k}|\)が極めて小さい領域以外の寄与はほとんどないと考えるので、積分区間を拡張し、全空間における積分としてよい。よって、
\begin{align*}
\frac{\langle \hat{H} \rangle}{n} &\cong \varepsilon_0 + \frac{3V_0}{(2\pi)^3)}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}dk_xdk_ydk_z\frac{\hbar\omega v_0|\mathbf{k}|}{e^{\beta\hbar v_0|\mathbf{k}|}-1}\\
&= \varepsilon_0 + \frac{3V_0}{(2\pi)^3}\int_{0}^{\infty}4\pi k^2dk\frac{\hbar\omega v_0k}{e^{\beta\hbar v_0k}-1}\\
&= \varepsilon_0 + \frac{3V_0}{2\pi\hbar^3v_0^3}\frac{1}{\beta^4}\int_{0}^{\infty}dx\frac{x^3}{e^x-1}\\
&= \varepsilon_0 + \frac{pi^2V_0}{10\hbar^3v_0^3}(k_BT)^4
\end{align*}
1行目から2行目への式変形では、被積分関数が\(|\mathbf{k}|\)の関数になっていることを用いて、積分を動径方向の積分に直した。ベクトル\(\mathbf{k}\)の集合が張る3次元空間において、\(|\mathbf{k}|\)原点からの距離を表す。3行目から4行目への式変形では、\(x=\beta\hbar v_0k\)とおき、積分の公式\(\int_0^{\infty}\frac{x^3}{e^x-1} = \frac{\pi^4}{15}\)を用いた。
これを温度で微分すれば、モル比熱が求まる。
\begin{align*}
C(T) &= \frac{d}{dT}\left(\frac{\langle \hat{H} \rangle}{n}\right)\\
&= \frac{2\pi^2k_B^4V_0}{5\hbar^3v_0^3}T^3
\end{align*}
以上より、デバイモデルにおいて、低温での比熱は\(T^3\)に比例することが分かった。
5. デバイによる補完式:”デバイの比熱の式”
デバイモデルでは、高温・低温での比熱の振る舞いを良く再現することができた。しかし、「十分高温」「十分低温」とは言えない、すなわち\(\beta\hbar\omega_{max}\)が1と比較してそれほど小さくなく、かと言って1よりもずっと大きいわけでもないような「中温」での比熱の振る舞いは、結晶構造や物質の種類に大きく依存する。よって、これらを統一的に1つの数式で表すことはできない。
しかし、中温領域も含む補完式として、シンプルな1変数の積分で表される、デバイの比熱の式がある。特に、高温・低温では、デバイモデルの比熱の振る舞いと一致するため、上の議論で扱った3重積分と比べればずっと扱いやすい。
デバイの比熱の式
$$C_D(T) =\frac{3V_0}{(2\pi)^3}\int_{0}^{k_{max}}4\pi k^2dk\frac{(\hbar v_0k)^2}{k_BT}\left\{2sinh\frac{\hbar v_0k}{2k_BT}\right\}^{-2}$$
ここで、\(|\mathbf{k}|\)の上限\(k_{max}\)は、積分する領域の体積が変わらないという条件
$$\int_{-\pi /a}^{\pi /a}\int_{-\pi /a}^{\pi /a}\int_{-\pi /a}^{\pi /a}d^3\mathbf{k} = \int_0^{k_{max}}dk4\pi k^2$$
が成り立つように決定される。立方体の体積\(\frac{8\pi^3}{a^3}\)と球の体積\(\frac{4\pi k_{max}^3}{3}\)が等しいとき、
$$k_{max} = \frac{(6\pi^2)^{1/3}}{a}$$
である。また、デバイ温度
$$T_D \equiv \frac{\hbar v_0k_{max}}{k_B}$$
を定義すれば、デバイの比熱の式は
$$C_D(T) = 9R\left(\frac{T}{T_D}\right)\int_0^{\frac{T_D}{T}}dx x^4\left(2sinh\frac{x}{2}\right)^{-2}$$
とシンプルに表現することができる。また、高温・低温それぞれの極限において
\[
C_D(T)=
\begin{cases}
\frac{12\pi^4R}{5}\left(\frac{T}{T_D}\right)^3 & (T \ll T_D)\\
3R & (T \gg T_D)
\end{cases}
\]
6. 比熱に関する議論のまとめ
- 古典統計力学を用いると、温度や物質に依らず、高温での固体結晶の比熱は3Rであるというデュロン=プティの法則を導出することができた。
- 量子力学を導入したアインシュタインモデルを用いることで、低温で急激に比熱が減少することが分かった。しかし、実験的な結果を完全に再現することはできなかった。
- そこで、結晶を構成する粒子たちの集団的な振動を加味したデバイモデルを導入した。
- デバイの比熱の式\(C_D(T)\)で、デバイ温度\(T_D\)に比べて十分に高温・低温における比熱の振る舞いを正確に表現することができた。
【参考】
「統計力学I」田崎晴明 著
コメント