1. UnionFindクラスの実装
UnionFindの概要及び,Pythonにおけるクラスの実装については,次の記事を参考にしました.

実装例
# No0
from collections import defaultdict
class UnionFind():
"""
Union Find木クラス
Attributes
--------------------
n : int
要素数
patents : list
指定した要素の親(1つ上の)要素を格納
指定した要素が根の場合は,
-(グループの要素数) を格納
=> sizeメソッドに反映
"""
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
"""
ノードxの根を見つける
"""
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
"""
木に新たな要素を併合(マージ)
Parameters
---------------------
x, y : int
併合するノード
"""
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x):
"""
xの属する木のサイズ
"""
return -self.parents[self.find(x)]
def same(self, x, y):
"""
x, yが同じ木に属するか判定
"""
return self.find(x) == self.find(y)
def members(self, x):
"""
xの属する木に属する要素をリストで返す
"""
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
"""
全ての根をリストで返す
"""
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
"""
グループの数を返す
"""
return len(self.roots())
def all_group_members(self):
"""
全てのグループの要素情報を辞書で返す
"""
group_members = defaultdict(list)
for member in range(self.n):
group_members[self.find(member)].append(member)
return group_members
def __str__(self):
"""
print(uf)で全てのグループの要素情報を簡単に出力する
"""
return '\n'.join(f'{r}: {m}' for r, m in self.all_group_members().items())2. ATC001 B – Union Find
問題
\(N\) 頂点の、単純とは限らない無向グラフを考えます。 初期状態では、頂点のみが存在し、辺は全く存在せず、全ての頂点が孤立しているとします。 以下の2種類のクエリが、\(Q\)回与えられます。
引用元:B – Union Find (atcoder.jp)
連結クエリ: 頂点Aと、頂点Bを繋ぐ辺を追加します。
判定クエリ: 頂点Aと、頂点Bが、連結であるかどうか判定します。連結であれば Yes 、そうでなければ No を出力します。
クエリを順番に処理し、判定クエリへの回答を出力して下さい。
UnionFindクラスの基本的なメソッドである
- unionメソッド…新たな辺をグラフに追加
- sameメソッド…入力値であるa, bノードが同じグループに属するかを判定
の練習問題です.これらの機能をそのまま使います.
解答例
n, q = map(int, input().split())
uf = UnionFind(n)
for _ in range(q):
p, a, b = map(int, input().split())
if p == 0:
uf.union(a, b)
else:
print("Yes" if uf.same(a, b) else "No")3. ABC177 D – Friends
問題
人1から人Nまでの \(N\) 人の人がいます。
「人\(A_i\)と人\(B_i\)は友達である」という情報が \(M\) 個与えられます。同じ情報が複数回与えられることもあります。
XとYが友達、かつ、YとZが友達ならば、XとZも友達です。また、\(M\) 個の情報から導くことができない友達関係は存在しません。
悪の高橋君は、この \(N\) 人をいくつかのグループに分け、全ての人について「同じグループの中に友達がいない」という状況を作ろうとしています。
最小でいくつのグループに分ければ良いでしょうか?
引用元:D – Friends (atcoder.jp)
- グループ(連結成分)の大きさの,最大値を求めるだけ.
UnionFindを知っていればこんなに簡単です.
解答例
n, m = map(int, input().split())
uf = UnionFind(n)
for i in range(m):
a, b = map(int, input().split())
a -= 1
b -= 1
uf.union(a, b)
print(max([uf.size(i) for i in uf.roots()]))4. ABC206 D – KAIBUNsyo
問題
\(N\) 項からなる正整数列 \(A=(A_1,A_2, \cdots A_N)\) が与えられます。
以下の操作を 0 回以上何度でも行える時、操作を最小何回行えば、\(A\) を回文にすることができますか?
- ある正整数の組 \((x, y)\) を選ぶ。その後、現在 \(A\) に含まれる \(x\) をすべて \(y\) に置き換える。
なお、この問題では、全ての整数 \(i \ (1\le i \le N) \)について、\(A_i=A_{N+1-i}\) が成り立つとき、またその時に限って、\(A\) が回文であると言います。
引用元:D – KAIBUNsyo (atcoder.jp)
- 数列の中で,両端,両端から2番目,両端から3番目…というように,対称な位置にある要素同士を比較する.
- 怪文書を作るために,比較した値が同じならそのままでよいが,異なる場合は,どちらかに合わせる必要がある.
以下の入力例の場合,
8
1 5 3 2 5 2 3 1外側から比較した場合,比較する値が異なるものは,(5, 3), (3, 2), (2, 5)です.この場合,これらを辺の情報とするグラフを書いてみれば,外側のノードの値を内側のノードの値に統一(青矢印の方向)していけばいいことが一目瞭然となります.なお,赤矢印の方向に値を変更してしまうと,余計な変更手順が増えてしまいます.

もう一つ例を見てみましょう.以下の入力例の場合
11
5 1 5 3 2 5 2 3 1 7 2先ほどと同様に,対称な位置の数値を比較すると,左右で値が異なる組は,(5, 2), (1, 7), (5, 1)です.
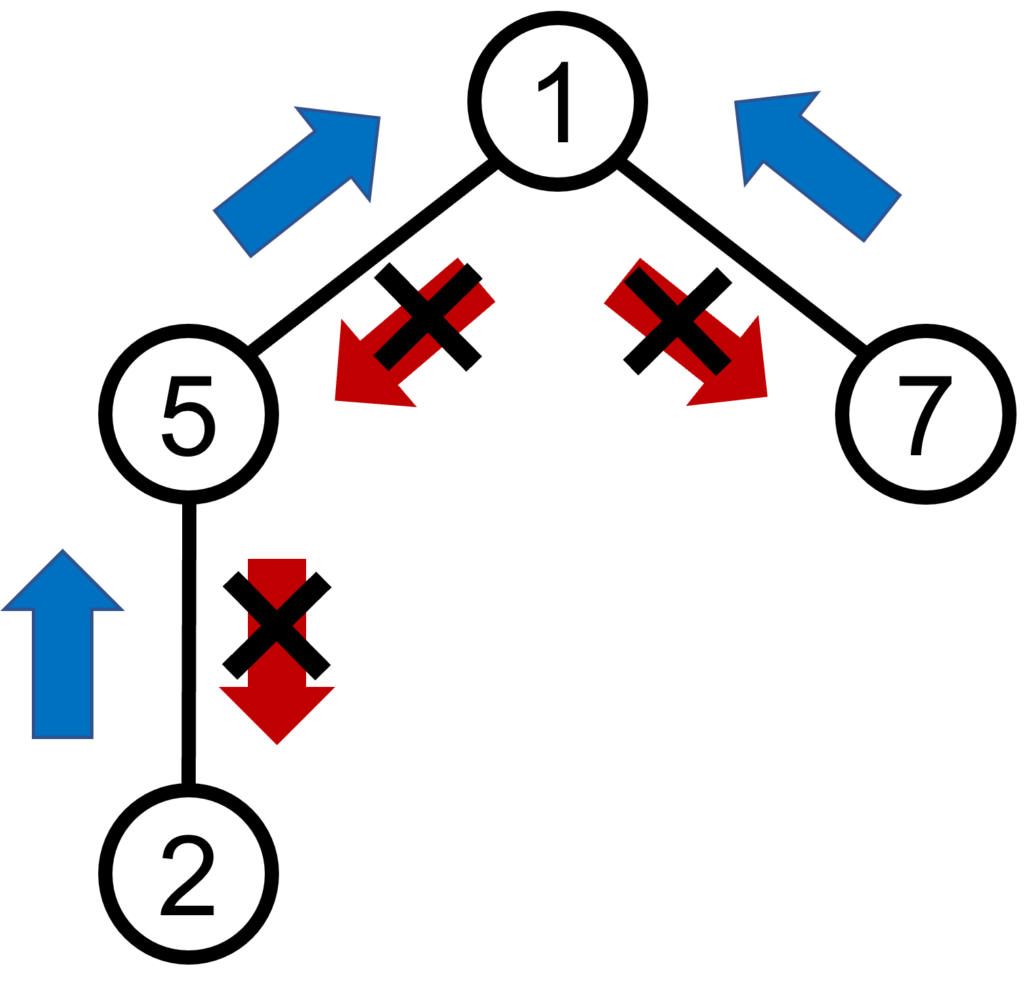
上記のようなグラフを作成し,UnionFindを用いて,次の操作を実現すればよいです.
- 各グループ(連結成分)の大きさを求める.
- 最小の変更回数は,各連結成分の大きさ(ノード数)- 1で求まる.
- 各連結成分における変更回数の総和をとる.
解答例
n = int(input())
a = list(map(int, input().split()))
es = set()
uf = UnionFind(2 * 10 ** 5) ###※(n)だと9ケースでエラーが発生
for i in range(n // 2):
if a[i] != a[n - 1 - i]:
uf.union(a[i] - 1, a[n - 1 - i] - 1)
ans = 0
for r in uf.roots():
if uf.size(r) >= 2:
ans += uf.size(r) - 1
print(ans)他の問題と違い,UnionFindオブジェクトの生成時,引数の指定に注意する必要があります.詳細はこちらの記事にて解説しています.
5. ARC106 B – Values
問題
\(N\) 頂点 \(M\) 辺の単純無向グラフが与えられます。 \(i\) 番目の辺は頂点 \(c_i\) と頂点 \(d_i\) を結んでいます。
はじめ、頂点 \(i\) には値 \(a_i\) が書かれています。あなたは次の操作を 0 回以上行うことで、操作後の各頂点の値をそれぞれ \(b_1,\cdots⋯,b_N\) にしたいと思っています。
- 辺を 1 つ選ぶ。選んだ辺が頂点 \(x\) と頂点 \(y\) を結んでいるとしたとき、次のいずれかを選んで行う。
- 値 \(a_x\) を -1 し、値 \(a_y\) を +1 する
- 値 \(a_x\) を +1 し、値 \(a_y\) を -1 する
適切に操作を行うことで目的を達成することが可能かどうかを判定してください。
引用元:B – Values (atcoder.jp)
- 操作を行っても,連結成分内の総和は不変.
- そして,あるパスを考えたとき,パスの両端の値を+1, -1にしつつパスの内部の値を変えないことが可能.つまり,隣り合う・合わないに限らず,任意の2頂点の間に操作をするのと同等のことができる.
- したがって,各連結成分について,始状態と終状態の,「ノードの持つ値の総和」さえ等しければ,目的を達成できる
上の,2つめのポイントに気づくのが難しいですが,きっと一度経験しておけば,他の問題で必要になったときにも,似たような発想ができるようになると思います.
解答例
n, m = map(int, input().split())
a = list(map(int, input().split()))
b = list(map(int, input().split()))
uf = UnionFind(n)
for i in range(m):
c, d = map(int, input().split())
c -= 1
d -= 1
uf.union(c, d)
flag = True
for c in uf.all_group_members().values():
if sum(a[i] for i in c) != sum(b[i] for i in c):
flag = False
break
print("Yes" if flag else "No")6. ABC049 D – 連結
問題
\(N\) 個の都市があり、\(K\) 本の道路と \(L\) 本の鉄道が都市の間に伸びています。 \(i\) 番目の道路は \(p_i\) 番目と \(q_i\) 番目の都市を双方向に結び、 \(i\) 番目の鉄道は \(r_i\) 番目と \(s_i\) 番目の都市を双方向に結びます。 異なる道路が同じ 2 つの都市を結ぶことはありません。同様に、異なる鉄道が同じ 2 つの都市を結ぶことはありません。
ある都市から別の都市に何本かの道路を通って到達できるとき、それらの都市は道路で連結しているとします。また、すべての都市はそれ自身と道路で連結しているとみなします。
鉄道についても同様に定めます。全ての都市について、その都市と道路・鉄道のどちらでも連結している都市の数を求めてください。
引用元:D – 連結 (atcoder.jp)
- UnionFindを用いると,道路網において,都市間の連結の有無を表現することができる.
- 同様に,鉄道網についても,都市間の連結をデータとして保持できる.
- 道路網あるいは鉄道網だけに着目したとき,ある連結成分の大きさ(要素数)を\(k\)とすると,sその連結成分(グループ)内で,各都市と連結している都市の数は,全ての都市について\(k\)となる.※本問では,ある都市について,自分自身とも連結していると考えるため.
解答例
from collections import defaultdict
n, k, l = map(int, input().split())
uf1 = UnionFind(n)
for i in range(k):
p, q = map(int, input().split())
uf1.union(p - 1, q - 1)
uf2 = UnionFind(n)
for i in range(l):
r, s = map(int, input().split())
uf2.union(r - 1, s - 1)
pairs = defaultdict(int)
# 各都市iについて,道路網および鉄道網において
# どの根のグループに属するかを調べる
for i in range(n):
pairs[(uf1.find(i), uf2.find(i))] += 1
for i in range(n):
print(pairs[(uf1.find(i), uf2.find(i))], end=" ")7. AtCoder ABC270 D – Unicyclic Components
問題
頂点に 1 から N の番号が、辺に 1 から M の番号がついた \(N\) 頂点 \(M\) 辺の無向グラフが与えられます。辺 \(i\) は頂点 \(u_i\) と頂点 \(v_i\)を結んでいます。
このグラフのすべての連結成分が次の条件を満たすかどうかを判定してください。
引用元:D – Unicyclic Components (atcoder.jp)
- その連結成分に含まれる頂点の個数と辺の本数が等しい。
詳しくはこちらの記事で解説しています.
解答例
n, m = map(int, input().split())
# 辺(エッジの全データを格納)
ed = []
# インスタンスを生成
uf = UnionFind(n)
for _ in range(m):
# 0-indexed
x, y = map(int, input().split())
x, y = x - 1, y - 1
# 新たなノードとエッジを追加
uf.union(x, y)
ed.append((x, y))
# 根をrとする連結成分(グループ)の辺の数を格納
es = {r: 0 for r in uf.roots()}
for x, y in ed:
# ノードx(yでも良い)の根を見つける
r = uf.find(x)
# 根rのグループに辺の数を+1
es[r] += 1
cond = all(uf.size(l) == es[l] for l in uf.roots())
print("Yes" if cond else "No")最後に
本記事では,ネットで調べたり,自分が過去に解いて印象に残ったUnionFind関連の問題を,ひとつのUnionFindクラスだけを使って解いてきました.今後も競技プログラミングを続けていく中で,本記事を補足・補強しうる問題に出会い次第,記事の内容を更新していく予定です.





コメント