木構造を扱う際、頂点間の距離や根からの距離を求めたり、木の直径を求めたりする場面があります。本記事では幅優先探索(BFS)の考え方を図で直感的にイメージした後、グラフ(木構造)の頂点間の距離に関する具体的な問題を解説しています。
幅優先探索のイメージをつかむ
- dequeに調べるべき頂点(ノード)を格納する。
- dequeの先頭nowをdeque.popleft()で取り出す。popの取り出しにより、dequeの2番目の要素が先頭に繰り上がる。
- nowに隣接する頂点群g[now]の要素nxtをすべて訪問し、訪問完了後dequeの末尾に加えていく。
- nowに関する調査は終わり。
- dequeの先頭(さっきは2番目の要素だったもの)を新たなnowとし、nowに隣接する頂点群g[now]の要素nxtをすべて訪問し、訪問完了後dequeの末尾に加えていく。
言葉だけでは分かりにくいので、図を使って考えてみます。
まず、根をnowとしてスタートし、根に隣接する頂点をg[now]=nextとします。

次に、next[0]を訪問し、根からの距離=1をリストdistに格納します。現在のnow(next[0])に隣接する未訪問の頂点が存在しないので、これ以上深くは進むことができません。

次にnext[1]を訪問します。根からの距離=1をリストdistに格納します。現在のnow(next[1])に隣接する未訪問の頂点が2つ存在するので、それら2つは訪問予定となります。


以後、上で行った操作を繰り返していけば、「根からの距離」=深さの小さい順に訪問し、根からの距離を求めることができます。



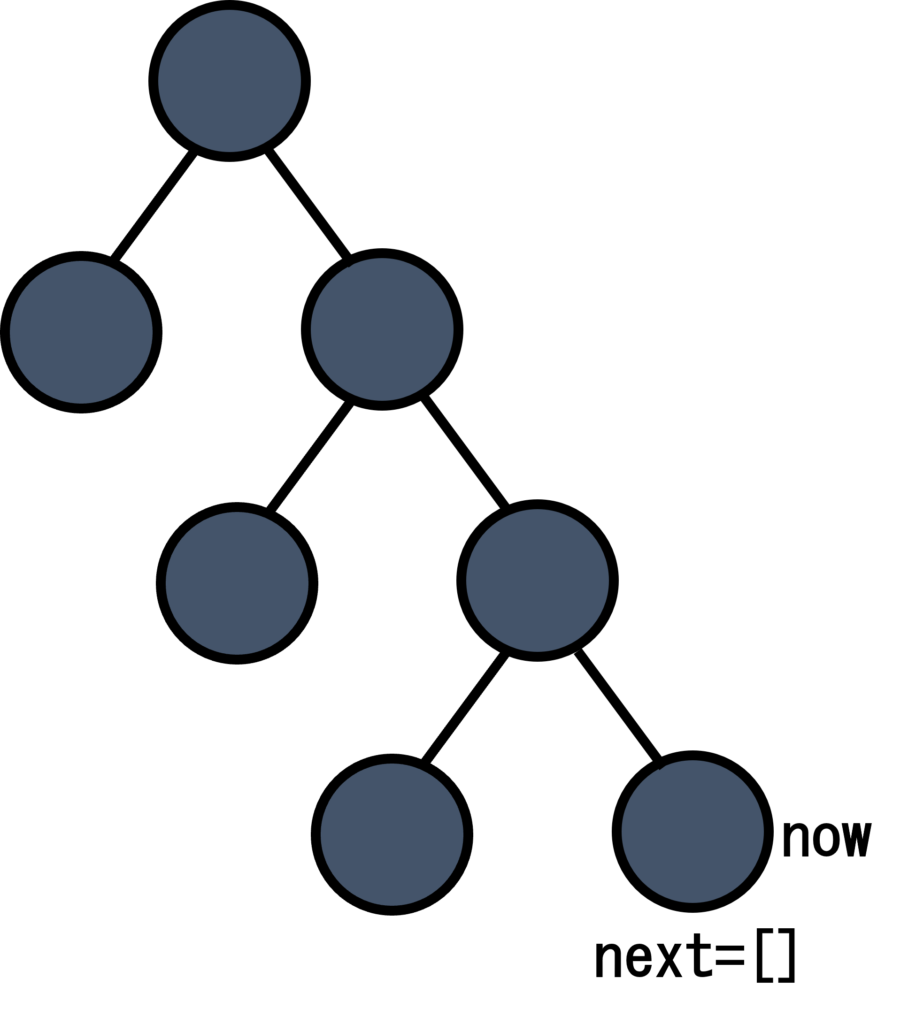
以上、幅優先探索で各頂点を訪問していく流れです。
1. 頂点間の距離を求める(根からの距離を求める)
木についての情報と頂点番号 A と整数 X が与えられるので、A から距離が X の全ての頂点の番号を昇順で出力してください。
引用元:https://paiza.jp/works/mondai/tree_primer/tree_primer__path
とある木構造についての情報(隣接する頂点番号の組a_i, b_i)と、根の頂点番号Aが与えられます。この時、頂点(根)Aからの距離がXである頂点をすべて出力せよという問題です。
ポイント
- グラフ(木構造)gを2次元リストで表現する。
- 各頂点の根からの距離を格納するリストdistを作成する。
- BFSで各頂点を訪問しながら根からの距離を求め、結果をdistに格納していく。
コード例
# 木構造において、根からの距離を求めたい
# 全ての頂点について A からの距離を求めるには A から幅優先探索を行えば良い
from collections import deque #幅優先探索のためのキュー
N, A, X = map(int, input().split())
# 木を表現する
g = [[] for _ in range(N)]
for _ in range(N - 1):
a, b = map(int, input().split())
a -= 1
b -= 1
g[a].append(b)
g[b].append(a)
q = deque()
q.append(A - 1)
# 各点の深さを格納するためのリスト(メモ: 全頂点が1列に並んでいたとしても絶対に超えない深さにする)
dist = [101] * N
# 頂点の深さは当然0
dist[A - 1] = 0
def BFS():
while q:
# 先頭を取り出してnowとする
now = q.popleft()
# nowと隣接する要素をすべて調べる
for nxt in g[now]:
# 未訪問なら距離を記録する
if dist[nxt] == 101:
dist[nxt] = dist[now] + 1
q.append(nxt)
BFS()
for i in range(N):
if dist[i] == X:
print(i + 1)2. 頂点間の経路を求める
木についての情報と頂点番号 A, B が与えられるので、A から B までの経路上の頂点を通る順に出力してください。なお、木においては異なる 2 頂点間を結ぶ経路は 1 通りに定まることが保証されています。
引用元:https://paiza.jp/works/mondai/tree_primer/tree_primer__path
頂点Aを根とし、頂点Bまでの経路を求めるに等しいと解釈できます。
ポイント
- グラフ(木構造)gを2次元リストで表現する。
- 各頂点に対し、1階層上(頂点Aが一番上とする)の頂点、すなわち親となる頂点のリストupperを作成する。
- BFSで各頂点を訪問しながら、頂点nxtの1階層上のnowをリストupperに格納していく。
- upperの要素は、BからAにさかのぼる順に格納されているので、最後は逆順で出力。
コード例
from collections import deque #幅優先探索のためのキュー
N, A, B = map(int, input().split())
# 木を表現する
g = [[] for _ in range(N)]
for _ in range(N - 1):
a, b = map(int, input().split())
a -= 1
b -= 1
g[a].append(b)
g[b].append(a)
q = deque()
q.append(A - 1)
upper = [-1] * N
# 頂点Aは根であることを, -2で表現する
upper[A - 1] = -2
def BFS():
while q:
now = q.popleft()
for nxt in g[now]:
if upper[nxt] == -1:
upper[nxt] = now
q.append(nxt)
BFS()
ans = []
now = B - 1
# 頂点
while upper[now] != -2:
ans.append(now)
now = upper[now]
# 最後に頂点をansに追加する
ans.append(A-1)
# ansにはB=>Aとたどる経路を格納したので, 逆順に出力する
for i in ans[::-1]:
print(i + 1)3. 木の直径を求める
ある木における、最も遠い 2 頂点間の距離をその木の直径といいます。
引用元:https://paiza.jp/works/mondai/tree_primer/tree_primer__diameter_of_tree
木 T についての情報が与えられるので、T の直径の値を求めてください。
ポイント
- 適当な頂点sから最も遠い頂点vを求める(BFS)。
※頂点vはグラフの性質(少々複雑な背理法で証明可能)により、木の直径を成す端点の1つになる。直感的な証明方法はないので、ここでは事実として扱う。 - よって、頂点vを根とし、vから最も遠い頂点uまでの深さを求めればよい(BFS, 問題の1. とほぼ同じ解き方)。
コード例
from collections import deque
# 頂点sからスタートする幅優先探索
def BFS(s):
dist = [-1] * N
dist[s] = 0
q = deque()
q.append(s)
while q:
now = q.popleft()
for nxt in g[now]:
if dist[nxt] == -1:
dist[nxt] = dist[now] + 1
q.append(nxt)
return dist
N = int(input())
g = [[] for _ in range(N)]
for _ in range(N - 1):
a, b = map(int, input().split())
a -= 1
b -= 1
g[a].append(b)
g[b].append(a)
# 頂点1(リスト内では0)からスタート
dist_from_zero = BFS(0)
# 頂点1からの最長距離を求める
max_dist = max(dist_from_zero)
for i, j in enumerate(dist_from_zero):
# 頂点1から最も遠い頂点jを探す
if j == max_dist:
diameter = max(BFS(i))
print(diameter)
break


コメント