【静電場】3. 円周・円板上に分布する電荷の作る電場を求める

輪の中心軸上における電場

半径Rの輪に, 一様な線密度$\lambda$で電荷が分布している場合の, 輪の中心軸上における電場を求める.

まず, 計算に使用するパラメータについて, 下図のように考える.

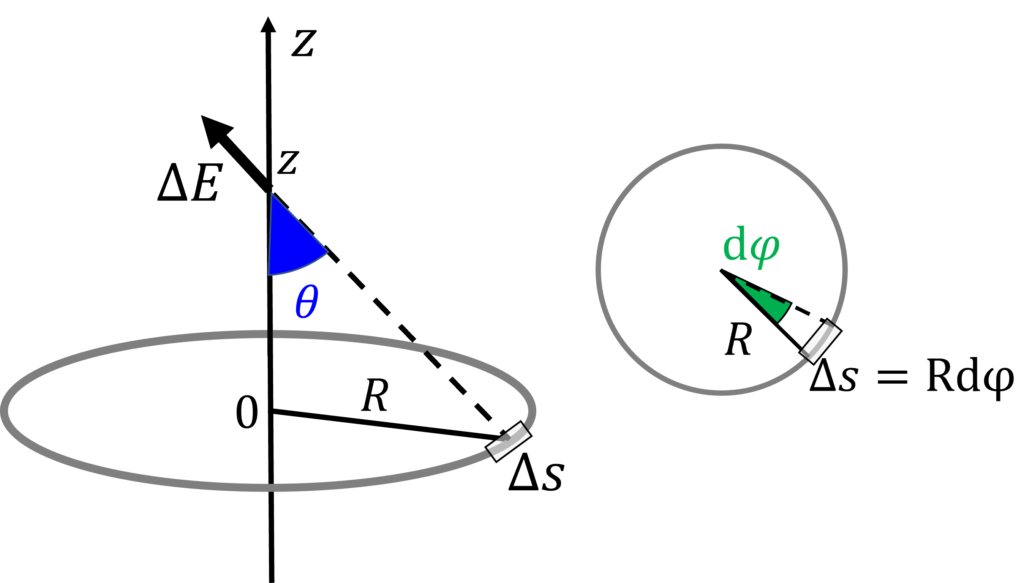
微小区間$\Delta s$が, 座標zで指定される軸上の点に作る電場$\Delta E$の大きさは

\begin{align*}
\Delta E &= |\Delta \mathbf{E}| \\
&= \frac{\lambda R \mathrm{d}\phi}{4\pi\varepsilon_0}\frac{1}{L^2}\\
&= \frac{\lambda R \mathrm{d}\phi}{4\pi\varepsilon_0}\frac{1}{R^2 + z^2}
\end{align*}

ここで, 微小区間による電場を, 輪の一周分足し合わせることで, z軸方向の成分のみが残る. なぜなら, 輪の180℃対称の位置の微小区間による電場のxy平面成分は, ちょうど打ち消し合うためである.

したがって, 求める電場はz成分のみとなり,

\begin{align*}
\mathbf{E} &= \int \Delta E cos\theta \mathbf{k}\\
&= \int \frac{\lambda R \mathrm{d}\phi}{4\pi\varepsilon_0}\frac{1}{R^2 + z^2}\left(\frac{z}{\sqrt{R^2 + z^2}}\right)\mathbf{k}\\
&= \frac{\lambda R \phi}{4\pi\varepsilon_0}\frac{z}{(R^2 + z^2)^{3/2}}\int_0^{2\pi} \mathrm{d}\phi\mathbf{k}\\
&= \frac{\lambda}{2\varepsilon_0}\frac{zR}{(R^2 + z^2)^{3/2}}i\mathbf{k}
\end{align*}

以上の計算結果を踏まえて, 物理的描像を考えると, 次のようになることが分かる.

電場は, $z > 0$で上向き.
$z = 0$で, 輪の上のあらゆる場所からの電場が互いに相殺しあい, 電場は0となる.
$z < 0$で下向き.

円板の中心軸上における電場

半径Rの円周上に, 一様な面密度$\sigma$で電荷が分布している場合の, 円板の中心軸上における電場を求める.

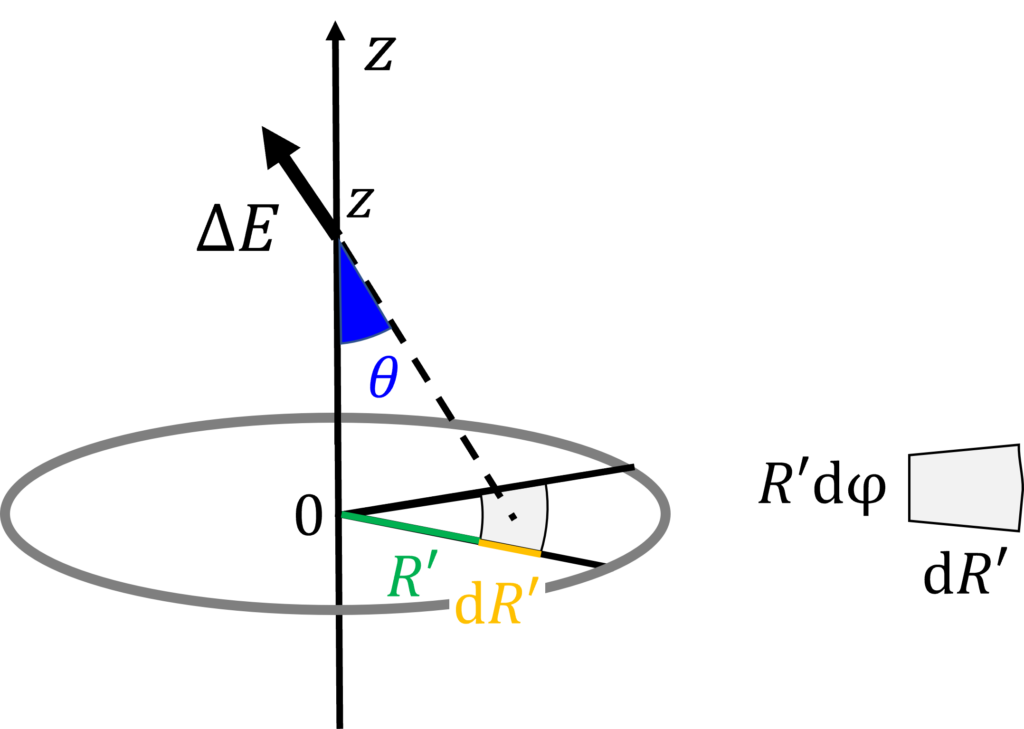
微小な長方形による電場$\Delta E$の内, 相殺されないz軸方向の成分を求めるには, $cos\theta$をかければよいので

\begin{align*}
\Delta cos\theta &= \frac{\sigma (R’\mathrm{d}\phi\mathrm{d}R’)}{4\pi\varepsilon_0}\frac{1}{R’^2 + z^2}\frac{z}{\sqrt{R’^2 + z^2}}\\
&= \frac{\sigma z}{4\pi\varepsilon_0}\int_{\phi = 0}^{\phi = 2\pi}\int_{R’ = 0}^{R’ = R}\frac{R’}{(R’^2 + z^2)^{3/2}}\mathrm{d}\phi\mathrm{d}R’\\
&= \frac{\sigma z}{4\pi\varepsilon_0}\int_{0}^{2\pi}\mathrm{d}\phi\int_{0}^{R}\frac{R’}{(R’^2 + z^2)^{3/2}}\mathrm{d}R’\\
&= \frac{\sigma z}{4\pi\varepsilon_0}\cdot 2\pi \cdot \left[\frac{-1}{\sqrt{R’^2 + z^2}}\right]_0^R\\
&= \frac{\sigma z}{2\varepsilon_0}\left(\frac{-1}{\sqrt{R^2 + z^2}} + \frac{1}{|z|}\right)
\end{align*}

以上の結果と, 電場のx, y 成分は０であることから

$$\mathbf{E} = \frac{\sigma z}{2\varepsilon_0}\left(\frac{z}{|z|} – \frac{z}{\sqrt{R^2 + z^2}}\right)\mathbf{k}$$

が得られる. ここで, 各項は次のような役割を持つと考えられる.