1. ガウスの定理とは
最初にガウスの定理を示しておこう.
$$\int_S\mathbf{E}\cdot\mathbf{n}dS = \int_V\nabla\cdot\mathbf{E}dV$$
これは,任意の平曲面S上での電場の面積分は,平曲面内部の領域Vの各位置における「発散」の体積積分と等しいことを表す.この物理的描像は最後に説明する.
2. 領域の結合についての性質
まず,隣接(結合)した2つの平曲面\(S_1, S_2\)のそれぞれの内部に存在する総電荷は\(Q_1, Q_2\)であるとする.また,2つの平曲面内の電荷の総和を\(Q = Q_1 + Q_2\)すると,ガウスの法則より,それぞれの平曲面について次の関係式が成り立つ.

\begin{align*}
\int_{S_1}\mathbf{E}\cdot\mathbf{n}dS = Q_1\\
\int_{S_2}\mathbf{E}\cdot\mathbf{n}dS = Q_2
\end{align*}
ここで,この2式の辺々を足し合わせてみよう.すると,ちょっと面白いことが分かる.まず,右辺の足し合わせは,言うまでもなく\(Q_1 + Q_2 = Q\)である.
また,2つの領域を結合させ,その表面(結合面は無視する)を平曲面Sと呼ぶと,ガウスの法則により
$$\int_{S}\mathbf{E}\cdot\mathbf{n}dS = Q$$
が成り立つ.つまり,
\begin{align*}
\int_{S_1}\mathbf{E}\cdot\mathbf{n}dS + \int_{S_2}\mathbf{E}\cdot\mathbf{n}dS\\
\ = \int_{S}\mathbf{E}\cdot\mathbf{n}dS
\end{align*}
が成り立たなければならない.
以上のことから,各領域においてガウスの法則が成り立つが,各領域についての電場の面積分の和は,結局,領域を結合してできる1つの平曲面についての電場の面積分に等しいということが分かった.
言い換えると,隣接した平曲面の面積分の和を取る時,結合面における面積分は相殺される.
ちなみに,平曲面\(S_1, S_2\)は,点Pにおいて同じ電場ベクトルを共有している一方で,\(S_1, S_2\)に立てた法線ベクトルの向きは互いに逆向きなので,境界の各点における面積分の和は0になる.

3. ガウスの定理を導出する
平曲面Sに囲まれた領域を,体積\(\Delta V_i\),面積\(\Delta S_i\)(\((i = 1, 2, ….)\), \(i\)は各領域に適当に付けた番号)を持った微小領域に分割する.
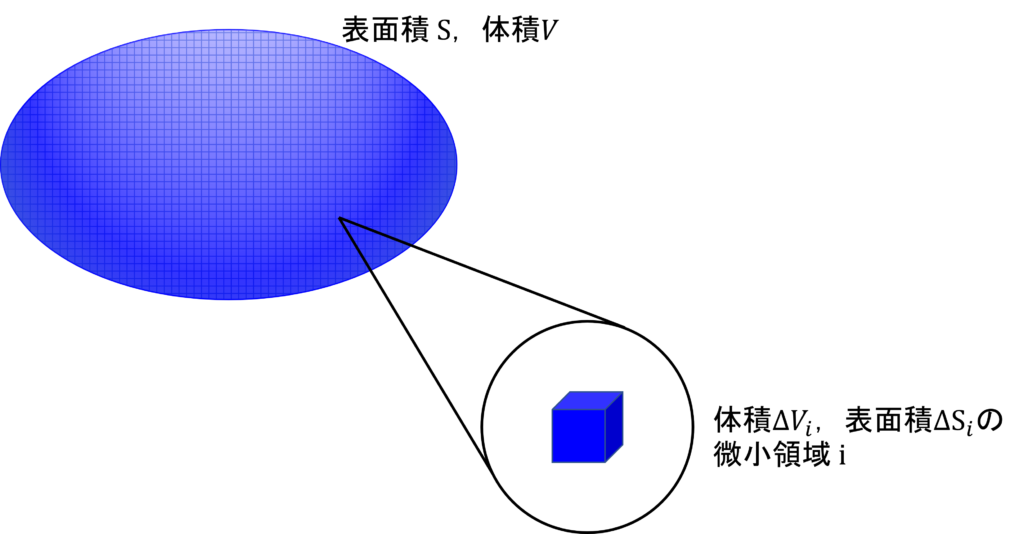
ガウスの法則は任意の領域で成り立つから,
で見たように,体積\(\Delta V\)の微小領域においては次式が成り立つ.
$$\int_S\mathbf{E}\cdot\mathbf{n}dS = \nabla\cdot\mathbf{E}\Delta V \ …(A)$$
ここで,2.で確認したように,隣接した平曲面の面積分の和を取る時,結合面における面積分は相殺されることを利用すると,次式が成り立つ.
$$\sum_i\left\{\int_{S_i}\mathbf{E}\cdot\mathbf{n}\Delta S_i\right\}= \sum_i\left\{\nabla \cdot \mathbf{E}(\mathbf{r}_i)\Delta V_i\right\}$$
さらに,\(\Delta V_i \rightarrow 0, \ \Delta S_i \rightarrow 0\)の極限をとることで,次のように書き換えることができる.これがガウスの定理である.
ガウスの定理
$$\int_S\mathbf{E}\cdot\mathbf{n}dS = \int_V\nabla\cdot\mathbf{E}dV$$
領域内部の各所における,電場という「流れ」の湧き出しの総和が,領域外に流出する流れの総和に等しいと解釈することができる.例えば,温泉の浴槽を1つの領域としてイメージしてみよう.浴槽の床や壁からは,常に新しいお湯が供給されている.これらの1つ1つが,\(\nabla\cdot\mathbf{E}dV\)に相当する「湧き出し」である.そして,浴槽の縁という境界(平曲面Sに相当)から単位時間あたりにあふれ出る流量は,すべての「湧き出し」における流量の総和である.
言い換えると,領域内部に局所的な湧き出しがいくつあったとしても,その総和は,領域外に出ていく流れの量だけを見ればわかるということである.
まとめ
先ほど挙げた記事では,式(A)を起点に,積分形ガウスの法則から「微分形ガウスの法則」を導いた.一方,本記事では,式(A)を中心として「ガウスの定理」を導出した.
微分形ガウスの法則の関係式を,積分形ガウスの法則に代入すれば,「ガウスの定理」になる.しかし,本記事の目的は,ガウスの定理が数式として成り立つことの単なる確認ではなかった.面積分に関する領域の結合の性質を用いることで,領域内部の湧き出しの総和(体積積分)が,領域の境界となる平曲面からの流出量と等しくなり,それが「ガウスの定理」の意味であることを理解したかったのである.
参考:物理入門コース「電磁気学I 電場と磁場」 長岡洋介



コメント