点Pにおかれた点電荷\(q\)による電気力線の内, 点Pを頂点とする頂角\(\theta_0\)の直円錐の底面Aを貫く電気力戦の数は, どれだけか. 総数Nに対する割合を求めよ.
[解]
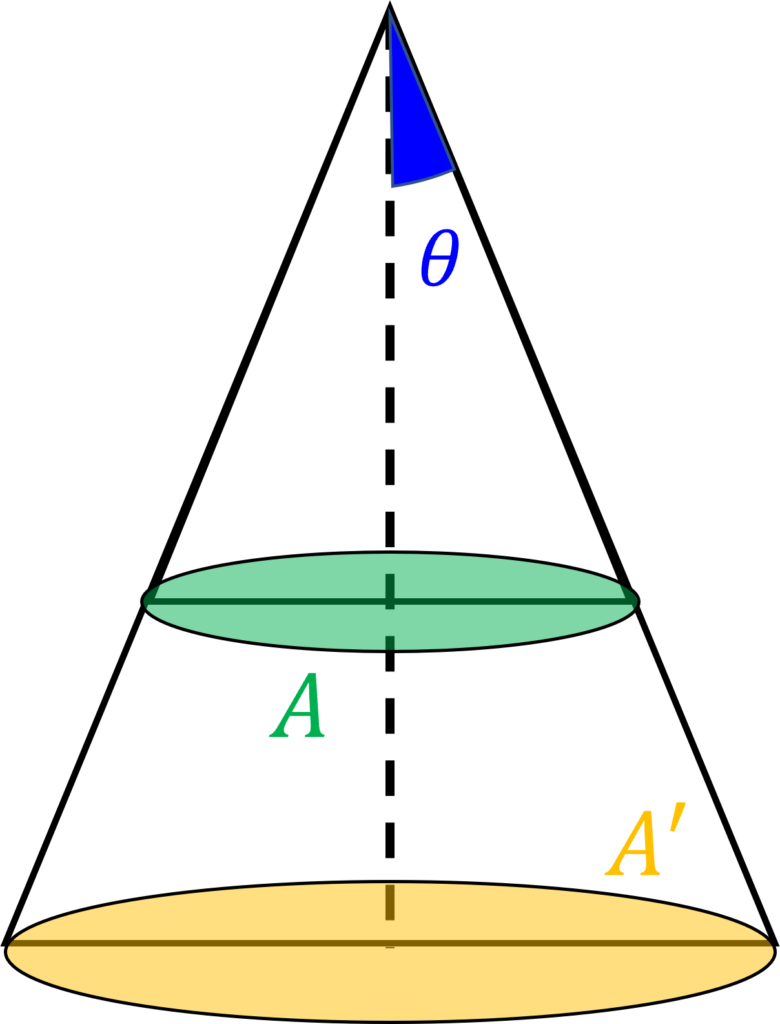
まず,異なる大きさの円錐が, 同じ頂角\(\theta = \theta_0\)を持つならば, 下図のように, 底面Aを貫く電気力戦の数は, A’ を貫く数と等しくなる. よって, ある頂角を持つ円錐を貫く電気力線の数は, 円錐の底面積の大きさに依存しない.
したがって, 問題の本質は, 電荷\(q\)を中心とする半径\(r\)の球の, 頂角\(\theta_0\)によって切りとられた部分の表面積(側面積は考えず, 球面部分のみ)を求めることである. すなわち, 頂角\(\theta_0\)に対応する, 立体角を求める問題に帰着する.
下図(A)の, 球面の内, 緑の断面より上の面積を求めたい. よって, 図(B)の微小な幅の帯を繋げていくような計算を考える.
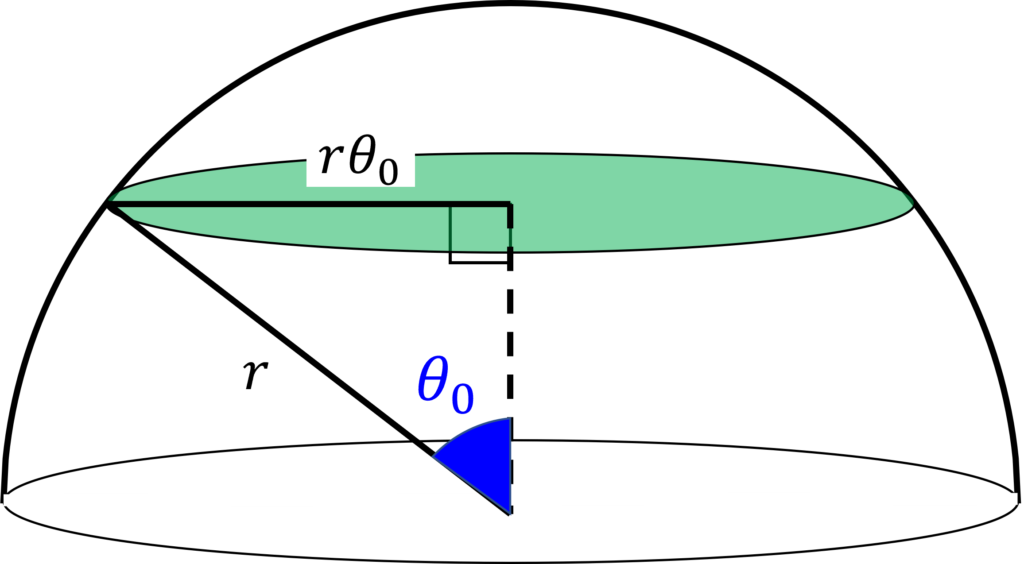
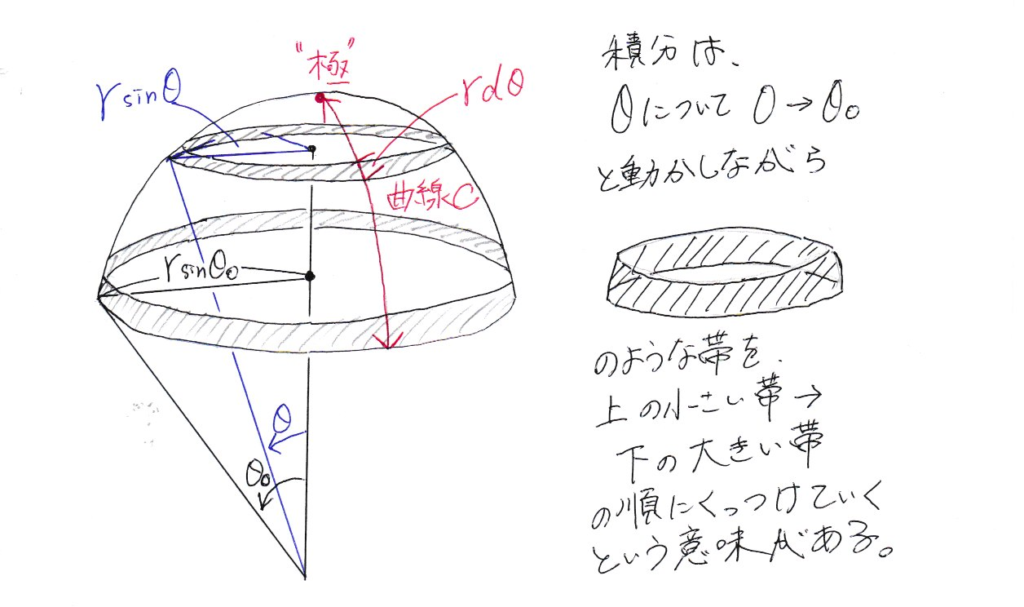
まず, 帯の長さは, 注目する帯が作る円周の長さ\(2\pi r sin\theta\)と等しい. 長さが最大となる帯は, \(\theta = \theta_0\)となる部分である. つまり, \(\theta = \theta_0\)の位置から, \(\theta < \theta_0\)の部分を(極に向かって)上に行くほど, 帯は短くなっていく.
次に, 切り口の端から極へ行く任意の曲線C上で考えれば, 帯の幅は\(r\mathrm{d}\theta\)と表すことができる.
以上より, 図Aの球面の一部の面積は, 帯の幅を\(\theta = 0\)から\(\theta = \theta_0\)にわたって足し合わせていけば求まるから,
\begin{align*}
&\int_0^{\theta_0} 2\pi r\mathrm{sin}\theta \ r\mathrm{d}\theta\\
& \ =2\pi r^2 \int_0^{\theta_0}\mathrm{sin}\theta\mathrm{d}\theta\\
& \ =2\pi r^2\left[-\mathrm{cos}\theta\right]_0^{\theta_0}\\
& \ =2\pi r^2(1 – -\mathrm{cos}\theta_0)
\end{align*}
となる. これを半径\(r\)の球の面積\(4\pi r^2\)で割ると, 所望の立体角
$$\frac{2\pi r^2(1 – -\mathrm{cos}\theta_0)}{4\pi r^2} = \frac{1}{2}(1 -\mathrm{cos}\theta_0)$$
が得られる.
求めた立体角は, 電気力線に総数に対する, 円錐を貫く電気力線の 割合そのものである.
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市著



コメント