半径\(r\)の球内に, 一様な密度\(\rho\)で分布する電荷が作る電場を求めよ.
[解]
電荷を持つ球と同じ中心を持つ半径\(r\)の球を考え, その球面S上での電場を求める.
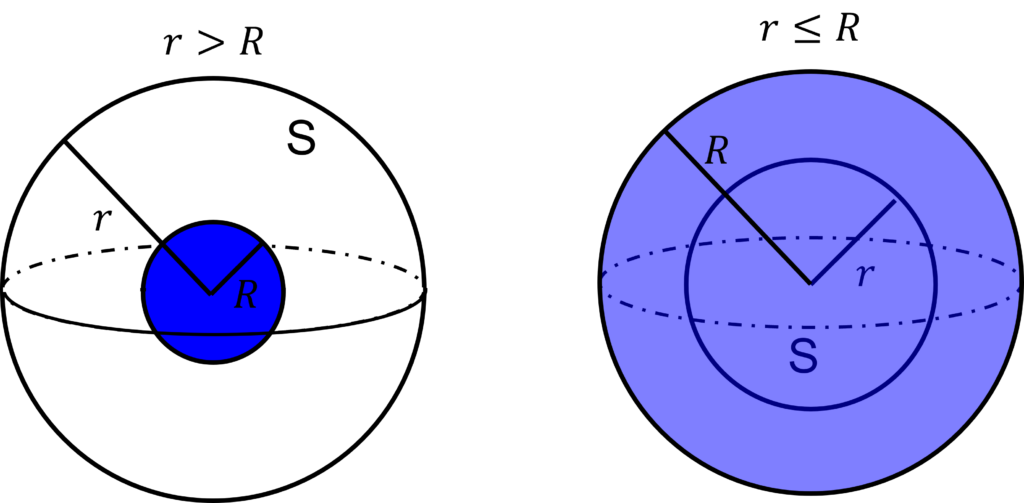
また, 図における青い領域は, 総電荷\(\frac{4}{3}\pi R^3 \cdot \rho\)が分布している領域を表している. 左図と右図で大きさが違って見えるように表現しているが, 実際は\(R\)は定数なので, 大きくなったり小さくなったりするのは\(r\)である.
i) \(r > R\)の場合, 球面Sの内部に, 全ての電荷を内包している. (下図左)
よって, ガウスの法則により,
\begin{align*}
\int_\mathrm{S}\mathbf{E}\cdot\mathbf{n}\mathrm{dS} &= E(r)\cdot 4\pi r^2\\
&= \frac{1}{\varepsilon_0}\frac{4}{3}\pi R^3 \cdot \rho
\end{align*}
以上より,
$$E(r) = \frac{\rho R^3}{3\varepsilon_0 r^2} \ …(1)$$
ii) \(r \le R\)の場合, (下図右)
球面Sに囲まれた部分の総電荷は, \(\frac{4}{3}\pi r^3 \cdot \rho\)である.
したがって, ガウスの法則を適用すると,
\begin{align*}
\int_\mathrm{S}\mathbf{E}\cdot\mathbf{n}\mathrm{dS} &= E(r)\cdot 4\pi r^2\\
&= \frac{1}{\varepsilon_0}\frac{4}{3}\pi r^3 \cdot \rho
\end{align*}
以上より,
$$E(r) = \frac{\rho r}{3\varepsilon_0} \ … (2)$$
また, (1), (2)は, \(r = R\)で一致することもわかる.
\[
E(r)=
\begin{cases}
\frac{\rho R^3}{3\varepsilon_0 r^2} & (r > R)\\
\frac{\rho r}{3\varepsilon_0} & (r \le R)
\end{cases}
\]
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市著



コメント