1. 積分形ガウスの法則の復習
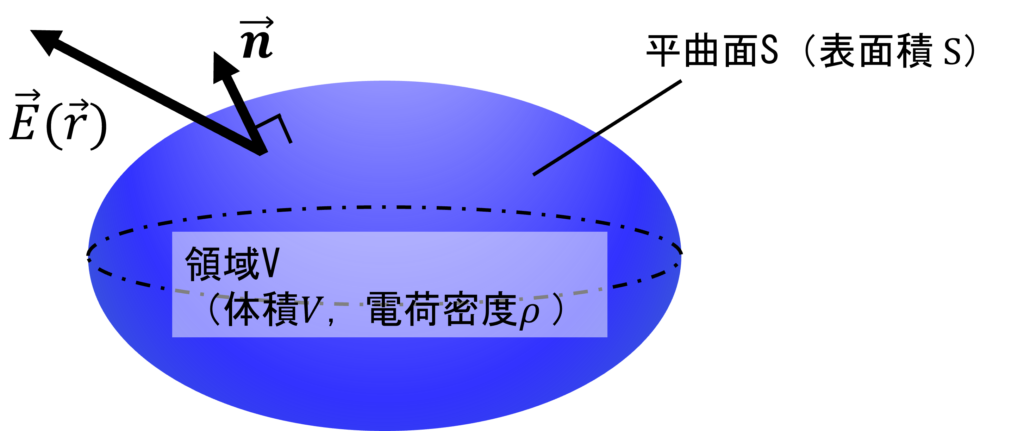
積分形ガウスの法則
真空中に点電荷(1式目)または空間的に連続分布する電荷(2式目)が存在するとき,任意の平曲面\(S\)上での電場の面積分と,平曲面に囲まれた空間\(V\)に含まれる総電荷量との間には,次の関係式が成り立つ.
\begin{align*}
\int_S \mathbf{E}\cdot\mathbf{n}dS = \frac{1}{\varepsilon_0}\sum_{i \in V}q_i\\
\int_S \mathbf{E}\cdot\mathbf{n}dS = \frac{1}{\varepsilon_0}\int_V\rho (\mathbf{r})dV
\end{align*}
ここで,ガウスの法則左辺の電場の面積分には,どのような物理的意味があるのだろうか?
それを理解するために,電場(電気力線)を,流れる水のような「流体」として捉えてみる.流体が,ある流速分布を持った流れているとき,位置\(\mathbf{r}\)における,局所的な流速を表すベクトルを\(\mathbf{u}\)とすると,
$$\int_S \mathbf{u}(\mathbf{r})\cdot\mathbf{n}(\mathbf{r})dS = [S内部から単位時間に湧き出す流量]$$
のように,「湧き出し」の量に関する等式が成り立つ.
電場のガウスの法則についても,電束密度\(\mathbf{D}(\mathbf{r}) \equiv \varepsilon_0\mathbf{E}(\mathbf{r})\)という物理量を定義することで
$$\int_S \mathbf{D}\cdot\mathbf{n}dS = Q$$
Qは平曲面S内部の総電荷
という関係が成り立つ.これは,ガウスの法則の法則の両辺に,真空の誘電率\(\varepsilon_0\)をかけたものと等しい.
なぜ流体の話を持ち出したのかというと,2.で単位体積当たりの湧き出し量を表す「発散」という演算子を扱うためである.電場と流体の類似性を知っておくことで,演算子の意味をイメージをしやすくなる.
2. 積分形から微分系ガウスの法則を導く
まず,真空中の任意(サイズ・形)の領域において,次の積分形ガウスの法則が成り立つのであった.
\begin{align*}
\int_S \mathbf{E}\cdot\mathbf{n}dS &= \frac{Q}{\varepsilon_0}\\
&= \frac{1}{\varepsilon_0}\int_V\rho (\mathbf{r})dV
\end{align*}
このとき右辺の\(Q = \int_V\rho (\mathbf{r})dV\)は,平曲面S内部(領域V)に存在する総電荷である.また,1.で考えたように,左辺の\(\int_S \mathbf{E}\cdot\mathbf{n}dS\)は,平曲面Sの内部から,Sの外部への「電場(という流れ)の湧き出し量」と解釈できる.ここで,ベクトル解析における「発散」演算子\(\nabla \cdot \)を用いると,ある場所\(\mathbf{r}\)における電場の「湧き出し」は次のように与えられる.
単位体積当たりの湧き出し量「発散」(div; divergence)
$$\nabla \cdot \mathbf{E} = \frac{\partial E_x}{\partial x} + \frac{\partial E_x}{\partial x} + \frac{\partial E_x}{\partial x}$$
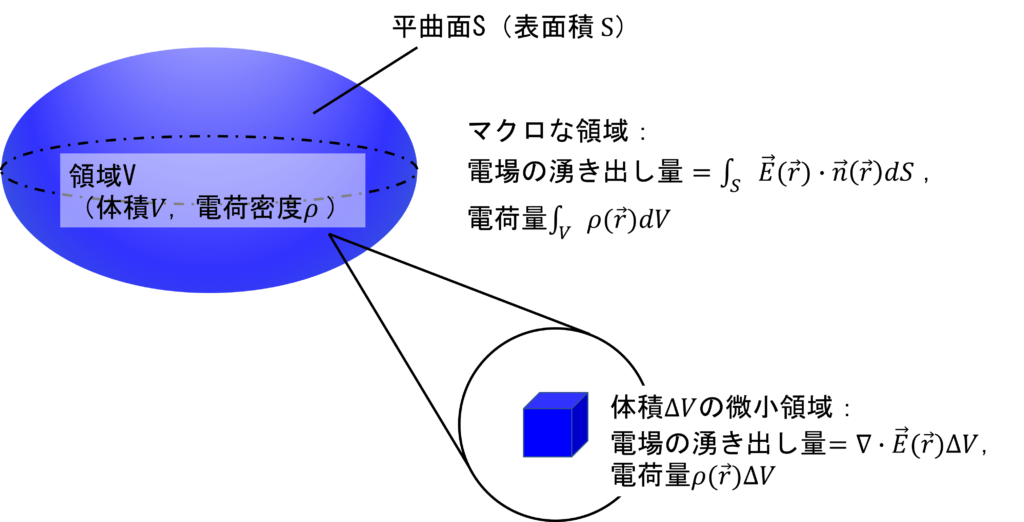
ここで,平曲面Sが囲む領域として,位置\(\mathbf{r}_0\)に存在し,体積\(\Delta V\)を持つ微小領域を選ぶ.位置\(\mathbf{r}_0\)における単位体積当たりの電場の湧出は\(\left[\nabla \cdot \mathbf{E}(\mathbf{r})\right]_{\mathbf{r} = \mathbf{r}_0}\)であるから,Sからの電場の「湧き出し」について,次の関係式が成り立つ.
$$\int_S \mathbf{E}\cdot\mathbf{n}dS = \left[\nabla \cdot \mathbf{E}(\mathbf{r})\right]_{\mathbf{r} = \mathbf{r}_0}\Delta V$$
また,領域が十分に小さければ,S内部における電荷の分布も\(\rho (\mathbf{r}) = \rho (\mathbf{r}_0) \)で一様であると見なせる.したがって,積分形ガウスの法則より,次の関係式が成り立つ.
$$\int_S \mathbf{E}\cdot\mathbf{n}dS = \frac{1}{\varepsilon_0}\rho (\mathbf{r}_0)\Delta V$$
この2つの関係式の右辺同士は等しく,等式で結ぶと,両辺から\(\Delta V\)を落とすことができる.したがって,平曲面Sの位置\(\mathbf{r}_0\)を,一般の位置\(\mathbf{r}\)に書き直すことで,
微分形ガウスの法則
$$\nabla \cdot \mathbf{E} (\mathbf{r}) = \frac{1}{\varepsilon_0}\rho (\mathbf{r})$$
または電束密度を用いて
$$\nabla \cdot \mathbf{D} (\mathbf{r}) = \rho (\mathbf{r})$$
が導き出される.少々長々と数式を追ってきたが,結果的には,積分形ガウスの法則と,電場の「湧き出し」との関係がシンプルな法則として得られた訳である.
参考:物理入門コース「電磁気学I 電場と磁場」 長岡洋介



コメント