静電場\(\mathbf{E}\)の中では, 電荷\(q\)には力\(q\mathbf{E}\)が働く.
電場によって電荷に働く静電力に逆らって, 電荷を微小距離\(\mathrm{d}s\)だけ動かすために必要な仕事を考える. すると, その大きさは「静電力に抗って電荷を動かすために必要な最小の力」と微小距離\(\mathrm{d}s\)の積で表される. 動かす方向の単位ベクトルを\(\mathbf{t}\)とすれば, 必要な仕事は\(-q\mathbf{E}\cdot\mathbf{t}\mathrm{d}s\)となる. ここで, 負号が付くのは, 「静電力に抗い, 静電力と同じ大きさ・逆向きの力を加えながら」電荷を動かすためである. また「必要な最小の力」というのは, 「電荷にかかる力が常につりあった状態を保つ」という意味である.
ここで, 任意の閉じた経路をCとして, Cに沿って上記のように「静電力に逆らって」電荷を一周させる. この時に要する仕事について, Cに沿った周回積分(線積分)を行う.
$$-q \displaystyle \oint_C \left\{\mathbf{E}(\mathbf{r})\cdot\mathbf{t}(\mathbf{r})\right\} = 0 \ …(1)$$
が成り立つ. ここで, 等式の右辺が0となるのは, 静電場の中にある電荷に働く力は, 保存力であるためである. すなわち, 電荷を一周させて同じ位置に戻ってくるのだから, 必要な仕事は正味0であるといういみである.また,上式は動かす電荷量に関わらず成り立ち,次式に示す「積分形渦なしの法則」とも呼ばれる.
積分形渦無しの法則
$$\displaystyle \oint_C \left\{\mathbf{E}(\mathbf{r})\cdot\mathbf{t}(\mathbf{r})\right\} = 0$$
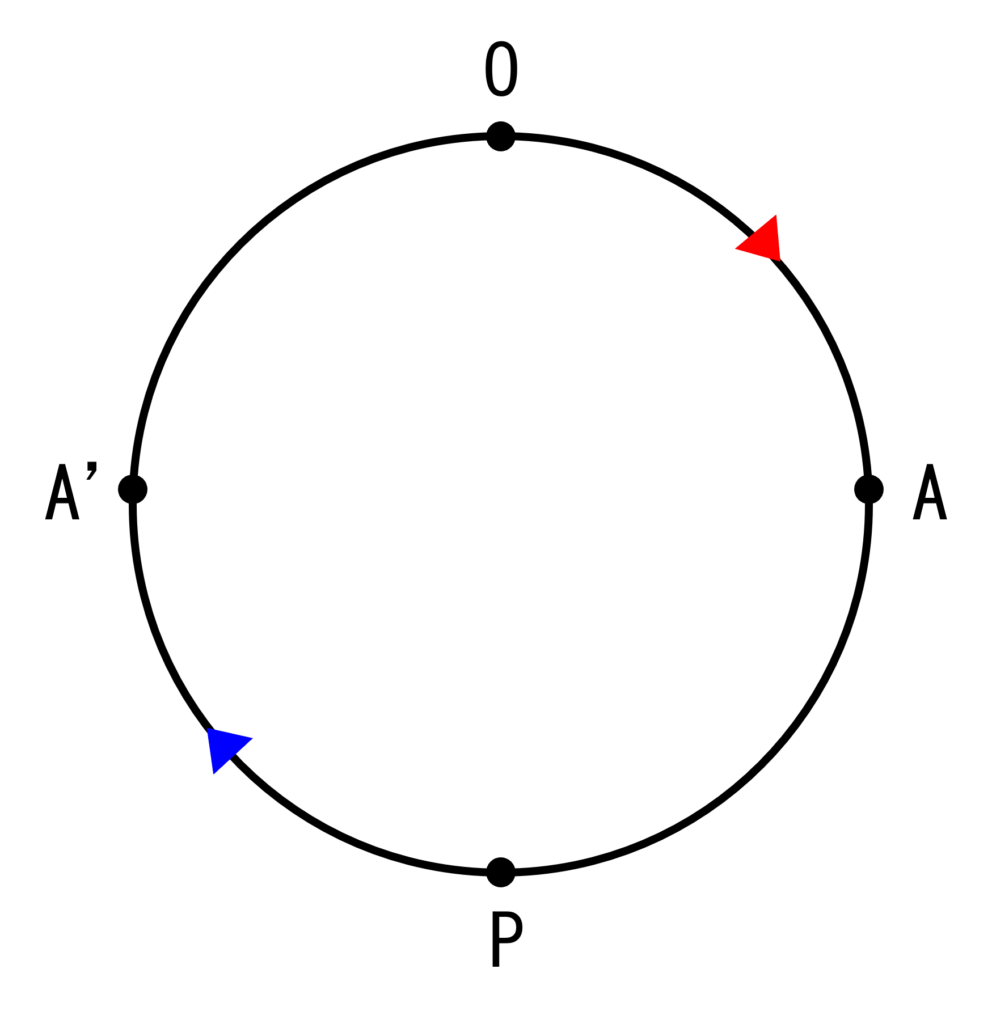
ここで, 下図のように, 経路Cを, 点Oから A ⇒ P ⇒ A’ を経てOに戻る経路とすると, (1)の関係は次のように書ける. 単に積分区間を点Pで区切ったという意味である.
$$-q\int_{\mathrm{OAP}}(\mathbf{E}\cdot\mathbf{t})\mathrm{d}s -q\int_{\mathrm{PA’O}}(\mathbf{E}\cdot\mathbf{t})\mathrm{d}s = 0$$
よって, 第二項を右辺に移項すれば, 次が成り立つ.
$$-q\int_{\mathrm{OAP}}(\mathbf{E}\cdot\mathbf{t})\mathrm{d}s = q\int_{\mathrm{PA’O}}(\mathbf{E}\cdot\mathbf{t})\mathrm{d}s$$
この等式の意味を考えると,
- 左辺は, 電荷\(q\)を点OからAを経由し, Pまで動かすために”要する”仕事.
- 右辺は, 電荷\(q\)を点OからA’を経由し, Pまで戻すために”要する”仕事の逆符号.
すなわち, 左辺は, 電荷が”外部に対してする仕事”.
と解釈することができる. これは, 仕事が正となる区間で初めに費やしたエネルギーが, その後の区間でそのまま戻ってくるようなイメージである.
そして, 費やしたエネルギーは, 電荷が点Pにある時, そこに蓄えられていると見なすことができる.
以上より, 静電場\(\mathbf{E}\)中の電荷\(q\)の持つ静電エネルギーとは, 点Oを基準(点Oでの値を0)とした, 点Pにある電荷の持つ位置エネルギーである. そして, 静電エネルギーを次のように表すことができる.
\begin{align*}
U_p &=-q\int_{\mathrm{OP}}(\mathbf{E}\cdot\mathbf{t})\mathrm{d}s \\
&=q\phi_p\\
&= q(\phi (P) – \phi (0)) \ …(2)
\end{align*}
ここで注意したいのは, 静電エネルギーは”相対的”な物理量であるという点である. 最後の式を見てわかるように, 点電荷の持つ電位は, 電荷の大きさと, 電位差の掛け算である. 電荷の値は, 何クーロンといった絶対的なものである. 一方, 電荷の位置点Pにおける電位差は, \(\phi_p = \phi (P) – \phi (0)\)という, 2点の電位の差で与えられる.
よって, 点Oについては, 電位が0となる点を選ぶのが一般的である.
では, 上で述べた静電場\(\mathbf{E}\)の中にある電荷の電位の場合, 電位の基準点Oはどこだろうか.
例えば, 静電場が点Bという点に存在する, 点電荷\(Q\)の作る電場である場合を考える. この場合, 電位が0となる点は, 点Bから無限遠にある点ということになる.
このように, 点電荷の持つ静電エネルギーを考えるとき, “無限遠を基準とする”のは大きなポイントである. これを踏まえて, 次の記事でより具体的な性質を見ていく.



コメント