問題はこちら。院試対策・物理学の勉強にご利用ください。
また、誤植があればお問い合わせください。
問1:同軸円筒形のコンデンサー
1-1.
導体内部では、電場がある限り電荷の移動が起こる。しかし、平衡状態では、内部に電場は存在しない。つまり、ガウスの法則により、導体内部には電荷が存在しないことが分かる。
1-2.
ガウスの法則により、
$$E(r)\cdot 2\pi rc = \frac{Q}{\epsilon_0}$$
$$E(r) = \frac{Q}{2\pi\epsilon_0rc}\cdot\frac{1}{r}$$
1-3.
導体間の電位差は
\begin{align*}
\Delta \phi &= – \int_b^aE(r)dr\\
&= \frac{Q}{2\pi\epsilon_0rc}log{b}{a}
\end{align*}
よって
$$C = \frac{Q}{\Delta\phi} =2\pi\epsilon_0c(log\frac{b}{a})^{-1}$$
1-4.
導体の持つ電荷が\( +q, -q\)のとき、\(\Delta q\)という小さな電荷を、外側の導体から内側の導体に運ぶために必要な仕事\(\Delta W\)は
\begin{align*}
\Delta W &= – \int_b^aE_q(r)\Delta qdr\\
&= – \int_b^a\frac{q\Delta q}2\pi\epsilon_0c\frac{1}{r}dr\\
&= \frac{q\Delta q}{2\pi\epsilon_0c}log\frac{b}{a}
\end{align*}
よって、\(q\)を\(0 \rightarrow Q\)とするために必要な仕事は
\begin{align*}
W &= \int \Delta W\\
&= \frac{1}{2\pi\epsilon_0c}log\frac{b}{a}\int_0^Qqdq\\
&= \frac{Q^2}{4\pi\epsilon_0c}log\frac{b}{a}
\end{align*}
1-5.
ガウスの法則より
$$\frac{Q}{\epsilon} = \frac{Q – Q_d}{\epsilon_0}$$
ここで、左辺は誘電体中においての電場の面積積分、右辺は真空中で「内側の導体の表面には\(Q – Q_d\)の電荷が存在する」として、電場の面積積分を考えた。よって
$$Q_d = \frac{\epsilon – \epsilon_0}{\epsilon}Q$$
問2:ソレノイドに作用する応力
2-1.
アンペールの法則より
$$B\cdot l = \mu_0 I\cdot N$$
$$B = \frac{\mu_0 IN}{l}$$
2-2.
\begin{align*}
\Phi &= B\cdot\pi r^2\cdot N\\
&= $$B = \frac{\mu_0 IN}{l}\cdot\pi r^2N\\
&= \frac{\mu_0 IN^2\pi r^2}{l}I\\
\end{align*}
よって
$$L = \frac{\Phi}{I} = \frac{\mu_0 IN^2\pi r^2}{l}$$
2-3.
$$\phi_{em} = – \frac{d\Phi}{dt} = – \frac{\mu_0 IN^2\pi r^2}{l}\frac{dI{t}}{dt}$$
これに抗して必要な電圧は\(\phi = \phi_{em}\)であり、必要な仕事は
\begin{align*}
J &= \int_{I=0}^{I=I}\phi Idt\\
&= L\int_0^II\cdot\frac{dI}{dt}dt\\
&= L\int_0^I\frac{1}{2}\left(\frac{dI^2}{dt}\right)dt\\
&= \frac{1}{2}LI^2
\end{align*}
2-4.
磁場のエネルギー密度は
\begin{align*}
u_m &= \frac{B^2}{2\mu_0}\\
&= \frac{\mu_0N^2I^2}{2l^2}
\end{align*}
よって、全エネルギーは
\begin{align*}
U_m &= u_m\times\pi r^2l\\
&= \frac{\mu_0N^2\pi r^2}{2l}I^2\\
&= \frac{1}{2}LI^2
\end{align*}
\(U_m = J\)であるので、ここまでの計算が正しいことが確認できた。
2-5.
ソレノイド中の磁場のエネルギーは
\begin{align*}
U &= \frac{1}{2}LI^2\\
&= \frac{1}{2}\frac{(IL)^2}{L}\\
&= \frac{1}{2}\frac{\Phi ^2}{L}
\end{align*}
よって、\(l \rightarrow l + \delta l (\delta l > 0)\)のようにソレノイドを引き延ばすことを考えたとき、\(U\)の変化量\(\delta U\)は
\begin{align*}
\delta U &= \frac{1}{2}\Phi ^2\cdot\frac{l + \delta l }{\mu_0N^2\pi r^2} – \frac{1}{2}\Phi ^2\cdot\frac{l}{\mu_0N^2\pi r^2}\\
&= \frac{1}{2}\Phi ^2\frac{\delta l }{\mu_0N^2\pi r^2}
\end{align*}
よって、ソレノイドに作用する応力\(F\)は
\begin{align*}
F &= – frac{\delta U}{\delta l}\\
&= – \frac{1}{2}\frac{\Phi ^2}{\mu_0N^2\pi r^2}
\end{align*}
この力は、負の符号が付いていることから、ソレノイドが縮もうとする向きであることが分かる。
問3:マクスウェル方程式
3-1.
$$div\mathbf{B} = \nabla\cdot (\nabla\times\mathbf{A}) = 0$$
\begin{align*}
rot\mathbf{E} &= – \nabla\times (\nabla\phi) – \frac{\partial}{\partial t}\nabla\times\mathbf{A}\\
&= 0 – \frac{\partial}{\partial t}\mathbf{B}\\
&= – \frac{\partial}{\partial t}\mathbf{B}
\end{align*}
3-2.
波動方程式の\(\frac{\partial ^2}{\partial t^2}\)の項の係数より\(v = \frac{1}{\sqrt{\epsilon_0\mu_0}}\)
3-3.
\(\nabla\cdot\mathbf{A} = 0\)が成り立つから、
\begin{align*}
\nabla\cdot\mathbf{A} &= \mathbf{A_0}\cdot (-k_xsin(\mathbf{k}\cdot\mathbf{r} – \omega t), -k_ysin(\mathbf{k}\cdot\mathbf{r} – \omega t), -k_zsin(\mathbf{k}\cdot\mathbf{r} – \omega t))\\
&= – \mathbf{A_0}\cdot\mathbf{k}sin(\mathbf{k}\cdot\mathbf{r} – \omega t) = 0
\end{align*}
すなわち、\(\mathbf{A_0}\cdot\mathbf{k} = 0\)であるから、\(\mathbf{A_0}\perp\mathbf{k}\), \(\mathbf{A}\perp\mathbf{k}\)が成り立つ。
\(\mathbf{A}\)は進行方向(\(\mathbf{k}\)の方向)に対して垂直なベクトルであるから、横波を表している。
3-4.
\begin{align*}
\mathbf{E} &= – \frac{\partial \mathbf{A}}{\partial t}\\
&= – \mathbf{A_0}\omega sin(\mathbf{k}\cdot\mathbf{r} – \omega t)
\end{align*}
\begin{align*}
\mathbf{B} &= \nabla\times\mathbf{A}\\
&= \nabla\times(A_{0x}cos(\mathbf{k}\cdot\mathbf{r} – \omega t), A_{0y}cos(\mathbf{k}\cdot\mathbf{r} – \omega t), A_{0z}cos(\mathbf{k}\cdot\mathbf{r} – \omega t))\\
&= (-A_{0z}k_ysin\theta + A_{0y}k_zsin\theta, -A_{0x}k_zsin\theta + A_{0z}k_xsin\theta, -A_{0y}k_xsin\theta + A_{0x}k_ysin\theta)\\
&= (A_{0y}k_z – A_{0z}k_y, A_{0z}k_x – A_{0x}k_z, A_{0x}k_y – A_{0y}k_x)sin(\mathbf{k}\cdot\mathbf{r} – \omega t)\\
&= \mathbf{A_0}\times\mathbf{k}sin(\mathbf{k}\cdot\mathbf{r} – \omega t)
\end{align*}
3-5.
\(\mathbf{S} = \overline{\mathbf{E}\times\frac{\mathbf{B}}{\mu_0}}\)である。ここで、次の計算をする。
\begin{align*}
\mathbf{E}\times\frac{\mathbf{B}}{\mu_0} &= – \mathbf{A_0}\omega sin(\mathbf{k}\cdot\mathbf{r} – \omega t)\times(\mathbf{A_0}\times\mathbf{k})sin(\mathbf{k}\cdot\mathbf{r} – \omega t)\cdot\frac{1}{\mu_0}\\
&= – \mathbf{A_0}\times(\mathbf{A_0}\times\mathbf{k})sin^2(\mathbf{k}\cdot\mathbf{r} – \omega t)\cdot\frac{\omega}{\mu_0}\\
&= A_0^2sin^2(\mathbf{k}\cdot\mathbf{r} – \omega t)\frac{\omega}{\mu_0}\mathbf{k}
\end{align*}
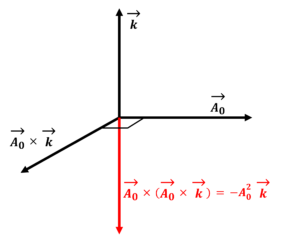
求めた\(\mathbf{E}\times\frac{\mathbf{B}}{\mu_0}\)の時間平均をとる。
\begin{align*}
\mathbf{S} &= \overline{\mathbf{E}\times\frac{\mathbf{B}}{\mu_0}}\\
&= \left\{\frac{A_0^2\omega}{\mu_0}\mathbf{k}\int_0^Tsin^2(\mathbf{k}\cdot\mathbf{r} – \omega t)dt\right\}\cdot\frac{1}{T}\\
&= \left\{\frac{A_0^2\omega}{\mu_0}\mathbf{k}\int_0^T\frac{1 – cos2(\mathbf{k}\cdot\mathbf{r} – \omega t)}{2}dt\right\}\cdot\frac{1}{T}\\
&= \frac{A_0^2\omega}{2\mu_0}\mathbf{k}
\end{align*}
一方、エネルギー密度\(u\)は
\begin{align*}
u &= \frac{\epsilon_0A_0^2\omega ^2}{2}\overline{sin^2(\mathbf{k}\cdot\mathbf{r} – \omega t)} + \frac{\epsilon_0A_0^2k^2}{2\mu_0}\overline{sin^2(\mathbf{k}\cdot\mathbf{r} – \omega t)}\\
&= \frac{A_0^2}{4}(\epsilon_0\omega ^2 + \frac{k^2}{\mu_0})\\
&= \frac{A_0^2\epsilon_0\omega ^2}{2}
\end{align*}
以上より
$$\frac{\mathbf{S}}{u} = \frac{\omega\mathbf{k}}{\mu_0\epsilon_0\omega ^2} = v\cdot\frac{\mathbf{k}}{|\mathbf{k}|}$$
すなわち
$$\mathbf{S} = u\cdot v\frac{\mathbf{k}}{|\mathbf{k}|}$$
となる。これは、単位面積を単位時間あたりに通過する電磁場のエネルギーを表している。



コメント