いくつかの記事を参考にしていますが、基本的に自力で解答することを目指しました。
今後に生かせるよう、汎用的で一般的な実装を行うことを心掛けました。
また、辞書的に利用できるよう、各問題に（個人的な）分類を記載しました。Ctrl + F のショートカットキーを使って、キーワードで問題を検索できます。
ABC250 C – Adjacent Swaps（リストの要素の紐づけ）
C - Adjacent Swaps
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- 毎回リスト内を探索するのでは時間がかかるので，以下のようなインデックスと数列の紐づけを行うことで対処する．
- インデックス（場所）から，数字を参照できるようにする．
- また，数字からインデックスを参照できるようにもする．
- これによって，場所の入れ替えに係るリスト内の要素参照だけで済む．
N, Q = map(int, input().split())
i_n = [i for i in range(N)] # インデックス（場所）から，数字を参照
n_i = [i for i in range(N)]
for _ in range(Q):
x = int(input())
x -= 1
if n_i[x] < N - 1: # 右端に居ない場合
tmp = n_i[x] # 数字xの現在の居場所
nxt_num = i_n[tmp + 1] # 右隣の数字
nxt_tmp = n_i[nxt_num] # 右隣の数字の現在の場所
n_i[x] = nxt_tmp
n_i[nxt_num] = tmp
i_n[tmp] = nxt_num # 数字xの居た場所に置く数字
i_n[tmp + 1] = x
else:
tmp = n_i[x] # 数字xの現在の居場所
nxt_num = i_n[tmp - 1] # 左隣の数字
nxt_tmp = n_i[nxt_num] # 左隣の数字の現在の場所
n_i[x] = nxt_tmp
n_i[nxt_num] = tmp
i_n[tmp] = nxt_num # 数字xの居た場所に置く数字
i_n[tmp - 1] = x
for i in range(N):
print(i_n[i] + 1, end=" ")ABC251 C – Poem Online Judge（多次元配列の複数キーでのソート）
C – Poem Online Judge (atcoder.jp)
- まずは「オリジナル」に定義される要素を抽出する．
- 抽出した要素を，得点=>提出順の優先度で並べ替える．この際，提出順は小さいほうが優先されるが，得点は大きいほうが優先されることに注意する．
from collections import Counter
N = int(input())
lists = [] # 全入力と，各要素の入力順を格納するリスト
cand = [] # オリジナルのpoemとして，候補(candidate)となる要素を格納
for i in range(N):
s, t = input().split()
lists.append([s, i, int(t)])
ctr = Counter()
for i in range(N):
poem = lists[i][0]
ctr[poem] += 1
if ctr[poem] == 1:
cand.append(lists[i])
# オリジナルな提出の中
cand = sorted(cand, key = lambda x:(-x[2], x[1])) # 得点は大きいほうが先頭になるよう負号を付ける
print(cand[0][1] + 1)ABC252 C – Slot Strategy
C – Slot Strategy (atcoder.jp)
結構込み入った問題なので，物事を独立した問題に分割して考える必要がある．
- ある数字に着目したとき，同じ位置に居ない数字同士は干渉しない.
# まずはどの数字で一致するかを固定して探索する
N = int(input())
time = [[] for _ in range(10)]
# cnt[i][j]は秒数jで表示される数字 i の個数
cnt = [[0] * 10 for _ in range(10)]
for _ in range(N):
# 文字列を受けとる
s = input()
for i in range(10):
# 一文字ずつ確認
sint = int(s[i])
# 出現回数を記録
cnt[sint][i] += 1
# リールをsintで止める時刻 = i + (出現回数 - 1) * 10
time[sint].append(i + (cnt[sint][i] - 1) * 10)
ans = 10 ** 10
for i in range(10):
ans = min(ans, max(time[i]))
print(ans)参考：
https://qiita.com/sano192/items/ddf7a6093ef66e723719
ABC253 C – Max – Min Query（カウント・優先度付きキュー）
C – Max – Min Query (atcoder.jp)
- カウンターは，Counter()もしくはdefaultdict(int)でも実装可能．
- 3つ目の分岐の際に，毎回ソートを行っていてはTLEになる．
- よって、，優先度付きキュー（heapq）を使用する．
- まず，heapqは最小値しか取り出せないので，負号を付けた最大値のheapqも作成しておく．
- 最大値（最小値）の候補を，実際に取り出せるかどうかのチェックは，その数字のカウント数で判断する．カウンターはO(1)で値を参照できるので便利．
import heapq
from collections import Counter
ctr = Counter()
Q = int(input())
mx = []
mn = []
for _ in range(Q):
q = list(map(int, input().split()))
if q[0] == 1:
x = q[1]
ctr[x] += 1
heapq.heappush(mx, -x)
heapq.heappush(mn, x)
elif q[0] == 2:
x, c = q[1:]
ctr[x] -= min(c, ctr[x])
else:
while ctr[mn[0]] == 0:
heapq.heappop(mn)
while ctr[-mx[0]] == 0:
heapq.heappop(mx)
print(-mx[0] - mn[0])参考：優先度付きキューの使い方
【Python】優先度付きキューの使い方【heapq】【ABC141 D】 – Qiita
ABC254 C – K Swap（ソート）
- i番目の要素は，i，i+K，i+2K…といった飛び飛びの場所しか移動できない．
- そして，K個ごとの飛び飛びの要素のグループは，スワップによって任意の順番に入れ替えることができる．
- つまり，上記のようなグループ内について，すべてのグループ内で昇順に並べ替えた結果，全体が昇順になるかどうかを判定すればよい．
- グループ数はK個となる．
N, K = map(int, input().split())
a = list(map(int, input().split()))
for i in range(K):
a[i::K] = sorted(a[i::K])
flag = True
for i in range(N - 1):
if a[i] > a[i + 1]:
flag = False
print("Yes" if flag else "No")ABC255 C – ±1 Operation 1（負の数を割ったあまり）
C – ±1 Operation 1 (atcoder.jp)
- Y = X – Aが，Dの倍数からどの程度離れているかを求める．
- Y % D，- Y % Dの両方を見て，よりDの倍数に近いほうを採用する．
# 255
X, A, D, N = map(int, input().split())
if D == 0:
ans = abs(X - A)
elif D > 0:
mi = A
ma = A + D * (N - 1)
if X < mi:
ans = mi - X
elif ma < X:
ans = X - ma
else:
X -= A
ans = min(X % D, - X % D)
else:
mi = A + D * (N - 1)
ma = A
if A < X:
ans = X - ma
elif X < mi:
ans = mi - X
else:
X -= A
ans = min(X % abs(D), - X % abs(D))
print(ans)ABC256 C – Filling 3×3 array（全探索）
C – Filling 3×3 array (atcoder.jp)
- 行（row）としてあり得る組み合わせを全列挙する．
- ３行の組み合わせを全部試して，列（column）方向の条件を満たすか調べる．
h1, h2, h3, w1, w2, w3 = map(int, input().split())
# 行としてあり得るものを全列挙
def make_row(h):
rows = []
for i in range(1, h-1):
for j in range(1, h-i):
rows.append([i, j, h-i-j])
return rows
r1 = make_row(h1)
r2 = make_row(h2)
r3 = make_row(h3)
# ３行の組み合わせを全部試して，列方向の条件を満たすか調べる
ans = 0
for i in r1:
for j in r2:
for k in r3:
if i[0]+j[0]+k[0] == w1 and i[1]+j[1]+k[1] == w2 and i[2]+j[2]+k[2] == w3:
ans += 1
print(ans)ABC257 C – Robot Takahashi（ソート）
C – Robot Takahashi (atcoder.jp)
- 2つのリストを展開して，2次元リストに変換するにはzip関数が便利．
- 単調に基準値Xを探索できるように，体重でデータをソートする．
N = int(input())
S = input()
W = list(map(int, input().split()))
SW = [[w, s] for w, s in zip(W, S)]
# 体重でソート
SW.sort()
sorted_S = []
sorted_W = []
for sw in SW:
sorted_W.append(sw[0])
sorted_S.append(sw[1])
# 全てを1と判定する場合を初期値とする
score = sorted_S.count("1")
tmp = score
for i in range(N):
w, s = sorted_W[i], sorted_S[i]
# Xをwよりも大きくしたときのscoreの変動
if s == "0":
tmp += 1
else:
tmp -= 1
# 次の数字も同じ値の場合
# Xの値は更新せずに，scoreの変動を計算する
if i < N-1 and w == sorted_W[i+1]:
continue
# 次の数字と異なる場合はscoreを更新
else:
score = max(score, tmp)
print(score)ABC258 C – Rotation（要素へのアクセス）
- insertではO(N)の計算量がかかる．
- dequeを使えば，pop(), appendleft()それぞれO(1)で実装可能．
- しかし, 両端以外の要素に対するインデックスによるアクセスはリストの方が有利．
- よってdeqは使わず, インデックスの位相をずらして取得することを考える．
N, Q = map(int, input().split())
S = input()
start = 0
for i in range(Q):
t, x = map(int, input().split())
if t==1:
# 先頭文字として認識する位置をずらす
start -= x
else:
idx = (start + x -1)%N
print(S[idx])ABC259 C C – XX to XXX（RunLength圧縮）
- abbccca => a : 1, b : 2, c : 3, a : 1のように登場する文字の種類と個数によって，文字列の情報を圧縮し，文字列S，Tを比較する．
- 解けた後で知ったが, RunLength圧縮と言うらしい．
- 条件分岐で２回’No’と出力するとREになるので気を付ける．
S = input()
T = input()
ls = [S[0]]
lt = [T[0]]
for i in range(1, len(S)):
if S[i] == ls[-1][0]:
ls[-1] += S[i]
else:
ls.append(S[i])
for i in range(1, len(T)):
if T[i] == lt[-1][0]:
lt[-1] += T[i]
else:
lt.append(T[i])
if len(ls)!=len(lt):
print("No")
else:
cnt = 0
for s, t in zip(ls, lt):
if s[0]==t[0]:
if (len(s) < len(t) and len(s) >= 2) or len(s)==len(t):
cnt += 1
print("Yes" if cnt == len(ls) else "No") ABC260 C – Changing Jewels（再帰）
C – Changing Jewels (atcoder.jp)
- 公式解説では再帰関数を用いているが，下記のようにも解ける．
- 高いレベルのものから0個になるように処理．
- 処理の順番にだけ気を付ける．
N, X, Y = map(int, input().split())
# 各レベルの宝石の個数を格納する
dicR = {}
dicB = {}
for i in range(N):
if i+1==N:
dicR[i+1] = 1
else:
dicR[i+1] = 0
dicB[i+1] = 0
for key in range(N, 1, -1):
if dicR[key] > 0:
dicR[key-1] += dicR[key]
dicB[key] += X*dicR[key]
if dicB[key] > 0:
dicR[key-1] += 1*dicB[key]
dicB[key-1] += Y*dicB[key]
print(dicB[1])ABC261 C – NewFolder(1)（カウント）
- 未だ存在しないキーに対応する値も格納できるdefaultdictが便利．
- defaultdictの引数としてintを渡すのを忘れないように．
from collections import defaultdict
N = int(input())
cnt = defaultdict(int) # 0に初期化
for i in range(N):
s = input()
if cnt[s] == 0:
print(s)
else:
print(s + "(" + str(cnt[s]) + ")")
cnt[s] += 1ABC262 C – Min Max Pair（場合分け・インデックスの利用）
数列の各要素について，
- まず，要素の値と，そのインデックスが一致する数を数える．
- 次に，値とインデックスが入れ替わっているペア（1, 5, 4, 3, 2なら5, 2と4, 3）の数を数える．
前者から2つを選んで任意のペアを作ることができるので，その総数をansに加える．そして，後者のペアは一意に決まるので，そのまま総数を足し合わせる．
インデックスと要素を同時に扱う際には，enumerate関数が便利．
N = int(input())
A = list(map(int, input().split()))
for i in range(N):
A[i] -= 1
cnt = 0
# インデックスと数列の値が一致するものを探す
for i, a in enumerate(A):
if a == i:
cnt += 1
ans = cnt * (cnt - 1) // 2
# インデックスと値が対になるペアを探す
for i, a in enumerate(A):
# 要素aをインデックスとする要素A[a]が
# 要素aのインデックスiに等しくなる場合
if A[a] == i and i < a:
ans += 1
print(ans)ABC263 C – Monotonically Increasing（組み合わせ）
C – Monotonically Increasing (atcoder.jp)
- M以下の自然数の内，N個を取り出す組み合わせの全列挙を行えばよい．
from itertools import combinations
N, M = map(int, input().split())
nums = [i + 1 for i in range(M)]
for comb in combinations(nums, N):
print(*comb)ABC264 C – Matrix Reducing（bit全探索）
C – Matrix Reducing (atcoder.jp)
- 最初は問題の記述通り，削除する行と列の組を全探索し，行と列をdelで削除しようとしたが，bit全探索でも解けることに気づいた．
- 各行について，残す（1），削除する（0）を表すビット列bit_hと，各列について同様のbit_wの全パターンをまず用意する．
- そして，各パターンについて，ビットシフトを使って一桁ずつ0or1をチェックしていく．
- 残す行にいてはリストrowを生成し，残す列はそこに格納していく．
- インデントが何か所も入ることになるため，リスト生成や，要素のappendのタイミングに気を付ける必要がある．
h1, w1 = map(int, input().split())
a = [list(map(int, input().split())) for _ in range(h1)]
h2, w2 = map(int, input().split())
b = [list(map(int, input().split())) for _ in range(h2)]
flag = False
# 全パターンのbit列の用意
for bit_h in range(1 << h1):
for bit_w in range(1 << w1):
leave = []
for i in range(h1):
# 行を残す場合
if bit_h >> i & 1 == 1:
# 行を生成する
row = []
# 行が存在する場合
for j in range(w1):
# 列を残す場合
if bit_w >> j & 1 == 1:
row.append(a[i][j])
leave.append(row)
if leave == b:
flag = True
break
print("Yes" if flag else "No")ABC265 C – Belt Conveyor（マスの移動）
C – Belt Conveyor (atcoder.jp)
- 訪問済みリストvisitedを用意する．
- それ以上訪問できなくなる，または無限に訪問が続くことを確認するまで，訪問した場所のフラグを立て（visited[i][j] = 1）while文を回す．
- 訪問済みのマスに再び訪れた場合，無限に訪問が続くことに相当．
H, W = map(int, input().split())
g = [list(input()) for _ in range(H)]
visited = [[0 for _ in range(W)] for _ in range(H)]
i = 0
j = 0
flag = True
while 1:
if visited[i][j]:
print(-1)
flag = False
break
visited[i][j] = 1
if g[i][j] == "U" and i != 0:
i -= 1
elif g[i][j] == "D" and i != H - 1:
i += 1
elif g[i][j] == "L" and j != 0:
j -= 1
elif g[i][j] == "R" and j != W - 1:
j += 1
# 各分岐の2つめの条件を満たさない（枠からはみ出す）場合
else:
break
if flag:
print(i + 1, j + 1)ABC266 C – Convex Quadrilateral（多角形領域内外判定）
詳しくはこちらの記事を参照．
import numpy as np
rect = []
for i in range(4):
rect.append(list(map(int, input().split())))
def in_triangle(recta):
a = (recta[0][0], recta[0][1])
b = (recta[1][0], recta[1][1])
c = (recta[2][0], recta[2][1])
d = (recta[3][0], recta[3][1])
# 原点から点へのベクトルを求める
vector_a = np.array(a)
vector_b = np.array(b)
vector_c = np.array(c)
vector_d = np.array(d)
# 点から点へのベクトルを求める
vector_ab = vector_b - vector_a
vector_ad = vector_d - vector_a
vector_bc = vector_c - vector_b
vector_bd = vector_d - vector_b
vector_ca = vector_a - vector_c
vector_cd = vector_d - vector_c
# 外積を求める
vector_cross_ab_ad = np.cross(vector_ab, vector_ad)
vector_cross_bc_bd = np.cross(vector_bc, vector_bd)
vector_cross_ca_cd = np.cross(vector_ca, vector_cd)
#print(vector_cross_ab_ad, vector_cross_bc_bd, vector_cross_ca_cd)
# 正だと中にある
return vector_cross_ab_ad > 0 and vector_cross_bc_bd > 0 and vector_cross_ca_cd > 0
ins = 0
for i in range(4):
data = []
for j in range(4):
idx = i + j
data.append(rect[(j+i)%4])
#print(data)
if in_triangle(data):
ins += 1
print("Yes" if ins == 0 else "No")ABC267 C – Index × A(Continuous ver.)（累積和）
C – Index × A(Continuous ver.) (atcoder.jp)
- 全ての考えうる連続部分列について，与式を一から計算する時間はない．
- そこで，先頭からM個の連続部列について与式の値を計算し，先頭を1つ右にずらしたときの差deltaを足していくことで，与式の値を更新していく．
- 累積和に似た考え方．
N, M = map(int, input().split())
A = list(map(int, input().split()))
ans = []
tot = sum([(i+1)*A[i] for i in range(M)])
sm = sum(A[:M])
for i in range(N-M+1):
if i == 0:
ans.append(tot)
else:
delta = M * A[i+M-1] - sm
tot += delta
ans.append(tot)
sm = sm + A[i+M-1] - A[i-1]
print(max(ans))ABC268 C – Chinese Restaurant（計算量）
C – Chinese Restaurant (atcoder.jp)
- 料理iに注目する．
- 料理iが条件を満たすためには，時計回りにj = p[i] – i回またはj-1, j+1回だけ移動させる必要がある．
- 3通りの移動パターンについては，for文で処理すればよい．
N = int(input())
p = list(map(int, input().split()))
# 移動回数ごとにスコアを記録
cnt = [0 for _ in range(N)]
for i in range(N):
j = (p[i] - i - 1 + N) % N # 負の数にならないように+N
for k in range(3):
cnt[(j + k) % N] += 1
ans = 0
for i in range(N):
ans = max(ans, cnt[i])
print(ans)ABC269 C – Submask（2進数・bit全探索）
- Nの2進数について，Nを構成している，各桁の10進数表記をtableに格納していく．
- tableに含まれる要素の内，0個以上を足し合わせることで，条件を満たす非負整数xとなる．
- tableに含まれる要素から0個以上を選ぶ方法は，bit全探索で網羅できる．
N = int(input())
# Nの2進数
bit_N = bin(N)
# Nの2進数を反転したもの
bit_N_rev = bit_N[::-1]
table = []
for i in range(len(bit_N)-2):
if bit_N_rev[i] == "1":
table.append(2 ** i)
# どれかを0回以上使う
# 最大15個の1に対して，使うor使わないのbit全探索
ans = []
# i = tableの各要素の使用の有無を
for i in range(1 << len(table)):
tmp = 0
for j in range(len(table)):
if i >> j & 1:
tmp += table[j]
ans.append(tmp)
print(*ans, sep="\n")ABC270 C – Simple path（BFS・DFS）☆
詳しくはこちらで解説しています．
- g[i]に，頂点 i に隣接する頂点を格納することでグラフ（木）を表現する．
- 出発点Xを根とし，根に近いほうからdeque()の末尾に加えていく．
- dequeの先頭から処理していくことで，根に近いほうから先に処理される．
- upperリストに，各頂点の１つ前（１つ根に近い頂点）を記録していく．
- upperリストを使い，終点Yから出発点Xまでに通った点を復元する．
from collections import deque
N, X, Y = map(int, input().split())
# 木の情報を2次元リストに格納
g = [[] for _ in range(N)]
for _ in range(N - 1):
a, b = map(int, input().split())
a -= 1
b -= 1
g[a].append(b)
g[b].append(a)
q = deque()
q.append(X - 1)
# 各要素の1つ上の要素（親）を格納
upper = [-1] * N
# 頂点Aは根であることを, -2で表現する
upper[X - 1] = -2
def BFS():
while q:
# 先頭を取り出してnowとする
now = q.popleft()
# nowと隣接する要素nxtをすべて調べる
for nxt in g[now]:
# 未訪問なら"nxtの1つ前の要素"=nowを記録する
if upper[nxt] == -1:
upper[nxt] = now
q.append(nxt)
BFS()
ans = []
now = Y - 1
while upper[now] != -2:
ans.append(now)
now = upper[now]
ans.append(now)
# ansにはY=>Xとたどる経路を格納したので, 逆順に出力する
for i in ans[::-1]:
print(i + 1, end=" ")ABC271 C – Manga（カウント・シミュレーション）
- まずは巻数の昇順に要素を並べる．
- 基本的に巻数の小さいほうから読んでいく．
- ある巻数を読めなくなったら，巻数の最も大きい2つを犠牲にして読む．
from collections import Counter
N = int(input())
A = sorted(list(map(int, input().split())))
ctr = Counter(A)
# 読んだ冊数
ans = 0
# 今読むかん
now = 1
lim = N
while True:
if ctr[now] and now <= lim:
ans += 1
now += 1
N -= 1
#print(now, "A")
elif N >= 2:
N -= 2
lim -= 1
ans += 1
now += 1
#print(now, "B")
else:
#print(now, "C")
break
print(ans)ABC272 C – Max Even
- 奇数2つの和の最大値と，偶数2つの和の最大値を（可能であれば）計算し，それらの比較を行う．
- 奇数や偶数の数が足りなければ，上の最大値の計算は行わない．
N = int(input())
A = list(map(int, input().split()))
# 降順に並べ替え
A = sorted(A, reverse=True)
# 奇数の和の最大値
odd = 0
# 奇数の数
cnt_o = 0
# 偶数の和の最大値
even = 0
# 偶数の数
cnt_e = 0
# 答えとなる値の有無
ans = False
for i in range(N):
if A[i] % 2 == 0 and cnt_e < 2:
even += A[i]
cnt_e += 1
if A[i] % 2 != 0 and cnt_o < 2:
odd += A[i]
cnt_o += 1
if cnt_o == 2 and cnt_e == 2:
ans = True
break
elif cnt_o == 2 or cnt_e == 2:
ans = True
print(max(even, odd) if ans else -1)ABC273 C – (K+1)-th Largest Number（二分探索・カウント）
C – (K+1)-th Largest Number (atcoder.jp)
- Aに含まれる要素の種類を，setで保持する（ソートもしておく）．
- 各要素Aiより大きい数の個数を，昇順整列済のsetを対象に二分探索を行うことで調べる．
import bisect
from collections import Counter
N = int(input())
A = list(map(int, input().split()))
sA = sorted(list(set(A)))
sl = len(sA)
ans = []
# 各Aiについて，自分より大きい値の種類数を調べる
for i in range(N):
ans.append(sl - bisect.bisect(sA, A[i]))
ctr = Counter(ans)
for i in range(N):
print(ctr[i])ABC274 C – Ameba（シミュレーション）
- 時系列順に追っていけば，存在するアメーバの情報だけが出てくる．
- 各アメーバの深さは，親のアメーバの持つ深さ+1．
- データ構造を絵にかいてみると分かりやすい．
N = int(input())
A = list(map(int, input().split()))
ans = [0] * (2 * N + 1)
for i, a in enumerate(A):
# 親の深さ+1
ans[2 * i + 1] = ans[a - 1] + 1
ans[2 * i + 2] = ans[a - 1] + 1
print(*ans, sep="\n")ABC275 C – Counting Squares（ベクトル）
C – Counting Squares (atcoder.jp)
解説 – AtCoder Beginner Contest 275
- 辺が決まれば正方形が決まる（辺の傾きの方向も決める必要がある）．
- 決め打った点(i, j)と，時計回りで隣の点(s, t)からなる辺を探索．
- 辺をベクトルとすれば，他の2点も決まる．
from itertools import product
S = []
for _ in range(9):
S.append(input())
ans = 0
# 重複ありの順列
#要素の集合と，出力の長さを引数にとる
for i1, j1, i2, j2 in product(range(9), repeat = 4):
# 決め打った点(i, j)と，時計回りで隣の点(s, t)
if i2 > i1 and j2 >= j1 and S[i1][j1] == S[i2][j2] == "#":
# 始点(i1, j1) => 終点(i2, j2)のベクトルに対応
di = i2 - i1
dj = j2 - j1
# 2点目とベクトルから3点目が決まる
i3 = i2 + dj
j3 = j2 - di
# 3点目とベクトルから4点目が決まる
i4 = i3 - di
j4 = j3 - dj
if 0 <= i3 < 9 and 0 <= j3 < 9 and 0 <= i4 < 9 and 0 <= j4 < 9:
if S[i3][j3] == S[i4][j4] == "#":
ans += 1
print(ans)ABC276 （辞書順・二分探索）
C – Previous Permutation (atcoder.jp)
辞書順でPの1つ前の数列を求めるには，
- 可能な限り先頭の方はPに一致させる．
- Pの末尾の方から見て，昇順になっている部分（増加部分列）の開始位置plを調べる．
- 昇順部分の1つ前の数字top_preと，昇順部分に含まれる数字の中でtop_preの次に小さいものを入れ替えるような実装を行う．
from bisect import bisect
N = int(input())
P = list(map(int, input().split()))
# 昇順な場所の解始点
pl = 0
for i in range(N-1, 0, -1):
if P[i - 1] < P[i]:
continue
else:
pl = i
break
# 昇順部分の1つ前の数字
top_pre = P[pl - 1]
# 昇順部分
use = P[pl:]
idx = bisect(use, top_pre)
# 昇順部分に含まれるtop_preより小さい数字で最大のもの
# -> 変更部分の次の先頭
top_nxt = use[idx - 1]
del use[idx - 1]
use.append(top_pre)
ans = P[:pl-1] + [top_nxt] + sorted(use, reverse = True)
print(*ans)ABC277 C – Ladder Takahashi（連結性判定・幅優先探索）☆
C – Ladder Takahashi (atcoder.jp)
- 連結性の判定 + 到達しうる階の最大値を求める.
- グラフで接続する階を管理する.
- 今回はインデックスの最大値が\(10^9\)と大きく, リスト型で保持するのは厳しい.
- 辞書型で必要なkeyに対してだけ, リスト型のvalueを保持すればよい.
from collections import deque
from collections import defaultdict
N = int(input())
# 木を表現する
g = defaultdict(list)
for _ in range(N):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
ans = 0
q = deque()
visited = set()
# 訪問先リスト
q.append(1)
# 訪問済みリスト
visited.add(1)
def BFS():
global ans
while q:
# 先頭を取り出してnowとする
now = q.popleft()
#print(now)
ans = max(ans, now)
# nowと隣接する要素をすべて調べる
for i in g[now]:
# 訪問済みの所は訪れなくて良い
if i not in visited:
q.append(i)
visited.add(i)
BFS()
print(ans)ABC278 C – FF（辞書）
- N行N列のリストを使うとREエラーとなる．
- 辞書を使うことで，必要な分だけデータを保持する．
from collections import defaultdict
N, Q = map(int, input().split())
dictionary = defaultdict(set)
for i in range(Q):
t, a, b = map(int, input().split())
if t == 1:
dictionary[a].add(b)
elif t == 2:
dictionary[a].discard(b)
elif t == 3:
if a in dictionary[b] and b in dictionary[a]:
print("Yes")
else:
print("No")ABC279 C – RANDOM（ソート）
- 各列の情報を持った2つのリストを作成する．行と列の転置に相当する．
- 2つのリストの比較は，ソートした後に各リストの同じインデックスの要素を比較することで実現可能．
H, W = map(int, input().split())
s_cols = ["" for _ in range(W)]
for row in range(H):
s = input()
for col in range(W):
s_cols[col] += s[col]
t_cols = ["" for _ in range(W)]
for row in range(H):
t = input()
for col in range(W):
t_cols[col] += t[col]
s_cols.sort()
t_cols.sort()
same = True
for col in range(W):
if s_cols[col] != t_cols[col]:
same = False
break
print("Yes" if same else "No")ABC280 C – Extra Character（全探索）
C – Extra Character (atcoder.jp)
- 2つの文字列について、先頭から一文字ずつ比較すればよい。
- ただし、最後の文字が挿入された文字である場合には注意。見落とすとWA。
S = input()
T = input()
for i in range(len(S)):
if S[i] != T[i]:
print(i + 1)
break
if i == len(S) - 1:
print(i + 2)ABC281 C – Circular Playlist（累積和・二分探索）
C – Circular Playlist (atcoder.jp)
- 問題の題名にもあるように，周期性のあるデータを扱うことになる．
- Tを1回の全曲の総再生時間，割った余りをphase（位相）として扱う．
- phaseが，再生時間の累積和のどこに位置するのかを二分探索する．
import itertools
import bisect
N, T = map(int, input().split())
A = list(map(int, input().split()))
acc_list = list(itertools.accumulate(A))
# Tを1回の全曲の総再生時間で割った余り
phase = T % acc_list[-1]
# phaseのacc_listへの挿入位置（実際に挿入はしない）
index = bisect.bisect(acc_list, phase)
played_time = phase
if index != 0:
played_time -= acc_list[index - 1]
print(index + 1, played_time)ABC282 C – String Delimiter（論理演算）
C – String Delimiter (atcoder.jp)
- opened（””が閉じているか？）というbool値を用意すれば，opendの真偽で，「,」を変更するか否かを簡単に判定できる．
- openedの真偽は，「”」が出てくるたびに反転させる必要がある．これは論理演算XORを使えば一行で実現可能．
N = int(input())
S = list(input())
closed = True
for idx in range(N):
char = S[idx]
if char == '"':
# bool値を反転させる
closed ^= True
if char == ',' and closed:
S[idx] = '.'
print("".join(S))ABC283 C – Cash Register
C – Cash Register (atcoder.jp)
- 0が連続で2つ出てきた場合は，1回分の操作で済むことに注目すればいい．
S = input()
zero_count = 0
ans = len(S)
for idx in range(1, len(S)):
if S[idx] == '0':
zero_count += 1
else:
zero_count = 0
if zero_count == 2:
zero_count = 0
ans -= 1
print(ans)ABC284 C – Count Connected Components（グラフ理論・UnionFind）
C – Count Connected Components (atcoder.jp)
- UnionFindクラスを使えば，連結成分（グループ）の数を返してくれる．
- 詳しくは以下の記事をご覧ください．
from collections import defaultdict
class UnionFind():
"""
Union Find木クラス
Attributes
--------------------
n : int
要素数
patents : list
指定した要素の親（1つ上の）要素を格納
指定した要素が根の場合は，
-(グループの要素数) を格納
=> sizeメソッドに反映
"""
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
"""
ノードxの根を見つける
"""
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
"""
木に新たな要素を併合（マージ）
Parameters
---------------------
x, y : int
併合するノード
"""
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x):
"""
xの属する木のサイズ
"""
return -self.parents[self.find(x)]
def same(self, x, y):
"""
x, yが同じ木に属するか判定
"""
return self.find(x) == self.find(y)
def members(self, x):
"""
xの属する木に属する要素をリストで返す
"""
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
"""
全ての根をリストで返す
"""
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
"""
グループの数を返す
"""
return len(self.roots())
def all_group_members(self):
"""
全てのグループの要素情報を辞書で返す
"""
group_members = defaultdict(list)
for member in range(self.n):
group_members[self.find(member)].append(member)
return group_members
def __str__(self):
"""
print(uf)で全てのグループの要素情報を簡単に出力する
"""
return '\n'.join(f'{r}: {m}' for r, m in self.all_group_members().items())
N, M = map(int, input().split())
union_find = UnionFind(N)
for _ in range(M):
u, v = map(int, input().split())
u -= 1
v -= 1
union_find.union(u, v)
print(union_find.group_count())ABC285 C – abc285_brutmhyhiizp
C – abc285_brutmhyhiizp (atcoder.jp)
- アルファベットからなる文字列を26進数として考える．
- アルファベットと数値の変換は，A~Zを格納した文字列と各文字の位置の対応を利用．
S = input()
alphabet = "0ABCDEFGHIJKLMNOPQRSTUVWXYZ"
ans = 0
for i in range(len(S)):
ans += alphabet.find(S[len(S) - i - 1]) * 26 ** i
print(ans)ABC286 C – Rotate and Palindrome（キュー）
C – Rotate and Palindrome (atcoder.jp)
- 1回目は操作A，2回目は操作B…といった操作の全パターンを試すのでは切りがない．
- 操作Bの文字の置き換えによって，必ず回文にすることができる．
- そこで，文字を移動する操作Aの回数を固定し，その移動回数に応じて，回文にするために必要な操作Bの回数を求めればよい．
- キューを使うことで，配列の先頭から要素を取り出して末尾に追加する操作が高速に．
- PyPy3で実行．Python3では実行時間が間に合わずTLEになる．
from collections import deque
N, A, B = map(int, input().split())
S = list(input())
que = deque(S)
# 回文にするために置き換える必要のある文字数
def replace_char_count(array):
# 部分的な回文（リストの先頭・末尾から対称な位置の文字が一致）になっていない文字の数
not_palindrome_count = 0
for i in range(len(array) // 2):
if array[i] != array[N - i - 1]:
not_palindrome_count += 1
return not_palindrome_count
ans = [B * replace_char_count(que)]
for move_count in range(1, N):
popped = que.popleft()
que.append(popped)
ans.append(A * move_count + B * replace_char_count(que))
print(min(ans))ABC287 C – Path Graph?（深さ優先探索・幅優先探索・UnionFind）☆
C - Path Graph?
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
以下の3つの条件を満たすかどうかを判定する
- 全ての頂点（ノード）が連結成分であるか
- 全ての頂点について，隣接する頂点が2つ以下であるか
- 辺の数がN-1個以下であるか
ここでは，深さ優先探索を使った場合の実装例を紹介します．幅優先探索，UnionFindを使用する場合はこちらをご覧ください．
import sys
sys.setrecursionlimit(10 ** 8)
N, M = map(int, input().split())
# i番目の要素には頂点iと隣接する頂点を格納
graph = [[] for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u -= 1
v -= 1
graph[u].append(v)
graph[v].append(u)
# 全要素が連結成分であるか
visited = [False] * N
def dfs(position):
visited[position] = True # 訪問済みにする
for adjacent_node in graph[position]:
# 未訪問の場合
if visited[adjacent_node] == False:
dfs(adjacent_node)
dfs(0) # どこからスタートしてもいいので0から探索を開始する
all_united = all(visited)
# 全頂点が2要素以下と結合しているか
united_with_two_or_less = True
for i in range(N):
if len(graph[i]) > 2:
united_with_two_or_less = False
break
# 辺の数がN-1であるかを踏まえて判定
if all_united and united_with_two_or_less and M == N - 1:
print("Yes")
else:
print("No")ABC288 C – Don’t be cycle（UnionFind）
C - Don’t be cycle
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
from collections import defaultdict
class UnionFind():
"""
Union Find木クラス
Attributes
--------------------
n : int
要素数
patents : list
指定した要素の親（1つ上の）要素を格納
指定した要素が根の場合は，
-(グループの要素数) を格納
=> sizeメソッドに反映
"""
def __init__(self, n):
self.n = n
self.parents = [-1] * n
def find(self, x):
"""
ノードxの根を見つける
"""
if self.parents[x] < 0:
return x
else:
self.parents[x] = self.find(self.parents[x])
return self.parents[x]
def union(self, x, y):
"""
木に新たな要素を併合（マージ）
Parameters
---------------------
x, y : int
併合するノード
"""
x = self.find(x)
y = self.find(y)
if x == y:
return
if self.parents[x] > self.parents[y]:
x, y = y, x
self.parents[x] += self.parents[y]
self.parents[y] = x
def size(self, x):
"""
xの属する木のサイズ
"""
return -self.parents[self.find(x)]
def same(self, x, y):
"""
x, yが同じ木に属するか判定
"""
return self.find(x) == self.find(y)
def members(self, x):
"""
xの属する木に属する要素をリストで返す
"""
root = self.find(x)
return [i for i in range(self.n) if self.find(i) == root]
def roots(self):
"""
全ての根をリストで返す
"""
return [i for i, x in enumerate(self.parents) if x < 0]
def group_count(self):
"""
グループの数を返す
"""
return len(self.roots())
def all_group_members(self):
"""
全てのグループの要素情報を辞書で返す
"""
group_members = defaultdict(list)
for member in range(self.n):
group_members[self.find(member)].append(member)
return group_members
def __str__(self):
"""
print(uf)で全てのグループの要素情報を簡単に出力する
"""
return '\n'.join(f'{r}: {m}' for r, m in self.all_group_members().items())
N, M = map(int, input().split())
union_find = UnionFind(N)
graph = [[] for _ in range(N)]
for _ in range(M):
u, v = map(int, input().split())
u -= 1
v -= 1
union_find.union(u, v)
graph[u].append(v)
graph[v].append(u)
print(M - N + union_find.group_count())ABC289 C – Coverage（集合・ビット全探索）
- ビット全探索によって，M個の集合を選ぶか選ばないかの状態を探索する．
- 各数字が1つ以上含まれているかを判定するために，和集合を求める．
N, M = map(int, input().split())
sets = []
for i in range(M):
c = int(input())
a = set(map(int, input().split()))
sets.append(a)
ans = 0
# stateを2進数としてみると、各桁の選ぶor選ばないの情報を保持している
for state in range(1, 2**M):
contained_nums = set()
for shift in range(M):
if ((state >> shift) & 1): # 集合を選ぶ場合
contained_nums |= sets[shift]
ans += len(contained_nums) // N
print(ans)ABC290 C – Max MEX（集合・ソート）
C - Max MEX
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- K個取り出す際に，同じ数値を取り出す必要はない．
- よって，与えられた配列からソートされた集合を作って，その先頭から見ていく．
- 0から始まる連続した並びが途切れるか，K個目に達したらループ終了．
N, K = map(int, input().split())
A = list(map(int, input().split()))
sorted_set = sorted(set(A))
MEX_found = False
for idx in range(min(K, len(sorted_set))):
if idx != sorted_set[idx]:
print(idx)
MEX_found = True
break
if not MEX_found:
print(sorted_set[idx] + 1)ABC291 C – LRUD Instructions 2（複数キーでのソート）
C - LRUD Instructions 2
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- 「始点と同じ座標に居たことがあるか」ではなく、「任意の座標に2回以上居たことがあるか」という問題であることに注意する．
- 居たことのある座標を全て保持して，重複する座標があるかを判定する．
- 2次元リストの各キーでソートし，隣り合う要素を比較すれば効率的．
N = int(input())
S = input()
direction = {'L':[-1, 0], 'R':[1, 0], 'U':[0, 1], 'D':[0, -1]}
positions = [[0, 0]]
for char in S:
x = positions[-1][0]
y = positions[-1][1]
x += direction[char][0]
y += direction[char][1]
positions.append([x, y])
sorted_positions = sorted(positions, key=lambda x:(x[0], x[1]))
returned = False
for idx in range(N - 1):
if sorted_positions[idx] == sorted_positions[idx + 1]:
returned = True
break
print("Yes" if returned else "No")ABC292 C – Four Variables（約数列挙）
C – Four Variables (atcoder.jp)
約数列挙のアルゴリズムについてはこちら．
- ABは1～N-1の値をとりうる．各ABの値に対して，CDはN-1～1をとりうる．
- 1～N-1の各々について，2つの数の積で表す場合の数を数える．
- ある数がAとBの積で表される場合のAとBの組み合わせは，約数の数そのもの．
- 1をA, Bの積で表す場合の数×N-1をC, Dの積で表す場合の数
$$\displaystyle\sum_{i = 1}^{N-1}(iをA, Bの積で表す場合の数)\times (N-iをC, Dの積で表す場合の数)$$
N = int(input())
# 約数を列挙する関数
def divisor(n):
ds = []
for i in range(1, int(n ** 0.5) + 1):
# nをiで割り切れる場合
if n % i == 0:
# iは約数
ds.append(i)
# n = i^2ではない場合
if i != n // i:
ds.append(n//i)
# 昇順に並べ替える
ds.sort()
return ds
lis = []
for i in range(1, N):
lis.append(len(divisor(i)))
lis_inv = lis[::-1]
ans = 0
for i in range(len(lis)):
ans += lis[i] * lis_inv[i]
print(ans)ABC293 C – Make Takahashi Happy（bit全探索）
C - Make Takahashi Happy
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- 全ての経路をどうやって探索するかがポイント．
- 下に移動を1，右に移動を0とすればよさそう．
- 順列全探索（H-1個の1とW-1個の0を含むすべての順列を求め，各順列について探索）をしようとしたが実行時間が長すぎた．
- ビット全探索によって全移動に対する方向を1or0で保持し，1と0の数が適切な場合にのみその状態を利用すればよい．
import itertools
H, W = map(int, input().split())
A = [list(map(int, input().split())) for _ in range(H)]
def bit_count(num):
return bin(num).count("1")
ans = 0
for state in range(2 ** (H + W - 2)):
if bit_count(state) != H - 1:
continue
x = 0
y = 0
path = [A[x][y]]
for shift in range(H + W - 2):
if (state >> shift) & 1:
x += 1
else:
y += 1
path.append(A[x][y])
ans += len(set(path)) // (H + W - 1)
print(ans)ABC294 C – Merge Sequences（複数キーでのソート）
C - Merge Sequences
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- 多次元リストを用意し，第何要素でソートするかを切り替える．
- 最初は，数列Cを数の大きい順でソート．ソート結果を各要素に追加．①
- 次に，配列Cの各要素の元々のインデックスでソート．②
- ②の各要素を順番に取り出し，①で追加した値を表示．
N, M = map(int, input().split())
A = list(map(int, input().split()))
B = list(map(int, input().split()))
C = [[a] for a in A] + [[b] for b in B]
for idx in range(N + M):
C[idx].append(idx) # 第2要素としてC内でのインデックスを追加
# 第一要素でソート
C.sort()
for idx_sorted in range(N + M):
C[idx_sorted].append(idx_sorted) # 第3要素としてsort済みC内でのインデックスを追加
C = sorted(C, key=lambda x:(x[1]))
C_ans = []
for c in C:
C_ans.append(c[2] + 1) # Cのソート後に何番目だったか
print(*C_ans[:N])
print(*C_ans[N:N+M])ABC295 C – Socks（カウント）
- アイテムごとにペアの数を数えて，ansに足し上げていくだけ．
from collections import Counter
N = int(input())
A = list(map(int, input().split()))
ctr = Counter(A)
ans = 0
for k, v in ctr.items():
ans += v // 2
print(ans)ABC296 C – Gap Existence（二分探索）
C - Gap Existence
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
from bisect import bisect
N, X = map(int, input().split())
A = list(map(int, input().split()))
A.sort()
found = False
for idx in range(N):
# A[idx]よりXだけ大きい要素のindexを取得
target = bisect(A, A[idx] + X) - 1
if A[idx] + X == A[target]:
found = True
break
print("Yes" if found else "No")ABC297 C – PC on the Table（文字列）
C - PC on the Table
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- Pythonで文字列は，含まれる文字を書き換えることはできないので，リストに変換してから使用する．
H, W = map(int, input().split())
strings = [list(input()) for _ in range(H)]
for string in strings:
for w in range(W - 1):
if string[w] == string[w + 1] == 'T':
string[w] = 'P'
string[w + 1] = 'C'
print(''.join(string))ABC298 C – Cards Query Problem（辞書型）
C - Cards Query Problem
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- 出力に必要なデータを用意する．
- 数字と，数字の入った箱リストの対応付けにはdefaultdictが便利．
from collections import defaultdict
N = int(input())
Q = int(input())
box = [[] for _ in range(N)]
num_dict = defaultdict(set)
for _ in range(Q):
query = list(map(int, input().split()))
i = query[1] - 1
if query[0] == 1:
j = query[2] - 1
box[j].append(i + 1)
num_dict[i].add(j + 1)
elif query[0] == 2:
print(*sorted(box[i]))
else:
print(*sorted(num_dict[i]))ABC299 C – Dango（全探索）
C - Dango
AtCoder is a programming contest site for anyone from beginners to experts. We hold weekly programming contests online.
atcoder.jp
- 出てくる文字によって処理を場合分け．
- 基本は’o’が出たら暫定結果を+1，’-‘が出たら暫定結果と最終結果用変数の値を比較，というのを繰り返していくだけ．
- ただし，文字列を前から順に見ていくので，’o’で終わる場合に，既に’-‘が出現しているかを知っておく必要がある（”-oooo”のような場合）．
N = int(input())
S = input()
ans = 0
temp = 0
bar_exists = False
for idx in range(N):
if S[idx] == 'o':
temp += 1
else:
ans = max(ans, temp)
temp = 0
bar_exists = True
if temp > 0 and bar_exists:
ans = max(ans, temp)
print(ans if ans > 0 else -1)
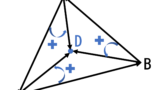
コメント