【静電場】2. 直線に分布する電荷の作る電場を求める

問題
２点A, B間の直線上に, 電荷が一様な線密度$\lambda$で分布しているとき, 直線から$r$の距離にある点Pに生じる電場$\mathbf{E}$を求めよ.

本記事では, 直線が無限に長い場合についても考察する.

解）

まず, 下の図のような状況を考える.

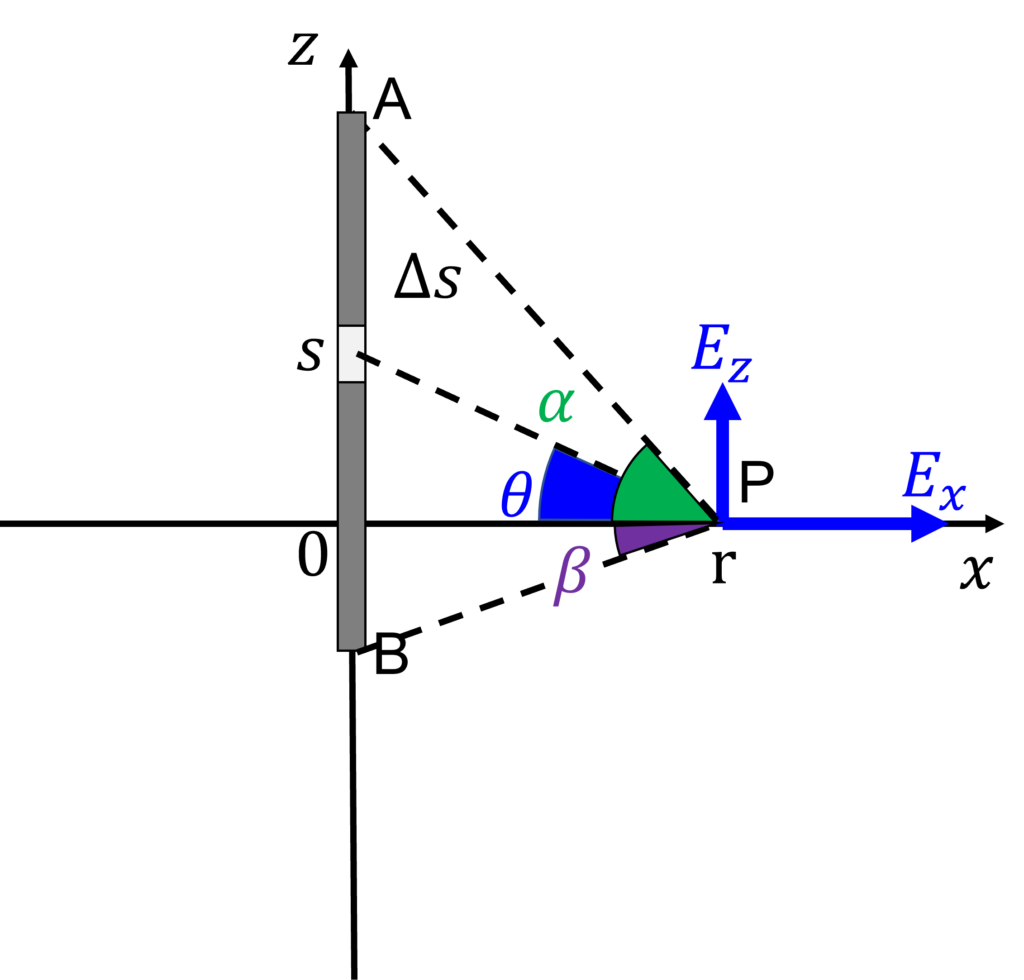
z軸上, $(0, 0, s)$の位置にある微小区間$\Delta s$によって点Pにできる電場は,

\begin{align*}
\Delta \mathbf{E} &= \frac{\lambda\Delta s}{4\pi\varepsilon_0}\frac{\vec{QP}}{QP^2}\\
&= \frac{\lambda\Delta s}{4\pi\varepsilon_0}\frac{1}{(s^2 + r^2)^{3/2}}(r, -s)\\
&=\Delta E_x \mathbf{i} + \Delta E_z \mathbf{k}
\end{align*}

よって, 電場のx, z成分のそれぞれについて,

$$E_x = \int_B^A \Delta_x= \frac{\lambda}{4\pi\varepsilon_0}\int_B^A\frac{r}{(s^2 + r^2)^{3/2}}ds$$

ここで, 積分区間を与えられていない（直線ABの長さを与えられていない）ので, $\mathrm{∠APO} =\alpha, \mathrm{∠BPO} = \beta, \ \mathrm{∠QPO} = \theta$と定める. また,

$$s = tan\theta \ \rightarrow \ ds = \frac{r}{cos^2\theta}d\theta$$

とおくことにより

\begin{align*}
E_x &= \frac{\lambda}{4\pi\varepsilon_0}\int_B^A\frac{r}{[r^2(tan^2\theta + 1)]^{3/2}}\cdot\frac{r}{cos^2\theta}d\theta\\
&= \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}\int_B^Acos\theta d\theta\\
&= \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}(sin\alpha – sin\beta),\\
& \ ( – \frac{\pi}{2} < \beta < \alpha < \frac{\pi}{2})
\end{align*}

ii)

\begin{align*}
E_z &= \int_B^A\Delta E_z\\
&= \frac{\lambda}{4\pi\varepsilon_0}\int_B^A\frac{-s}{(s^2 + r^2)^{3/2}}ds\\
&= \frac{\lambda}{4\pi\varepsilon_0}\left[\frac{1}{(s^2 + r^2)^{1/2}}\right]_B^A\\
&= \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}[cos\theta]_\beta^\alpha\\
&= \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}(cos\alpha – cos\beta),\\
& \ ( – \frac{\pi}{2} < \beta < \alpha < \frac{\pi}{2})
\end{align*}

i), ii) の計算結果より

\begin{align*}
\mathbf{E} &= E_x\mathbf{i} + E_y\mathbf{k}\\
&= \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}(sin\alpha – sin\beta)\mathbf{i}\\
& \ + \ \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}(cos\alpha – cos\beta)\mathbf{k}
\end{align*}

が得られる.

ここで, $\lambda > 0$, すなわち正の電荷が分布していることを仮定し, この計算結果の妥当性を検討してみよう.

$- \frac{\pi}{2} < \beta < \alpha < \frac{\pi}{2}$であることから, $E_x$は常に正の値をとる. 図からも, 必ずx軸の正の方向を向くことが読み取れる.

$E_z$は, 電荷の分布が点Pの存在するx軸より上に寄っているとき負, 下に寄っているときは正となるから, 直感的に図から読み取れる状況と矛盾しない.

直線が無限に長い場合

よくネット上で,

直線が無限に長い場合はどうなるのでしょうか.
ガウスの法則を使わずに, 無限長の場合の電場を求めたい.

といった質問を見かけるので, 上で求めた式を用いて考えていく.

\begin{align*}
\mathbf{E} &= \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}(sin\alpha – sin\beta)\mathbf{i}\\
& \ + \ \frac{\lambda}{4\pi\varepsilon_0}\frac{1}{r}(cos\alpha – cos\beta)\mathbf{k}
\end{align*}

において, 第一項は直線に垂直な成分である. 一方, 第二項は直線に平行な成分である.

$- \frac{\pi}{2} < \beta < \alpha < \frac{\pi}{2}$という条件下で, 直線が無限に長い場合を考えると, $\beta \cong -\frac{\pi}{2}, \alpha \cong \frac{\pi}{2}$となる. イコールとしないのは, $\alpha, \beta$は原点O, 点P, 直線の両端A, Bとのなす角であり, 厳密には直角にはならないからである. しかし, 直線が無限に長く, A, Bが無限に遠ければ, ほぼ$\beta = -\frac{\pi}{2}, \alpha = \frac{\pi}{2}$となる.

そして, ２つの角度の値を電場の式に代入すると,

\begin{align*}
\mathbf{E} &= \frac{\lambda}{2\pi\varepsilon_0}\frac{1}{r}\mathbf{i}
+0\cdot\mathbf{k}\\
&= \frac{\lambda}{2\pi\varepsilon_0}\frac{1}{r}\mathbf{i}
\end{align*}

となり, 直線に垂直な成分だけが残る. これは, 後に