【静電エネルギー】4. 連続分布する電荷の持つ静電エネルギー（積分形式）の導出

前回の記事

では, 離散的な点電荷の集合に対して, 静電エネルギーを求めた. 今回の記事では, 電荷がポツンと離散的に分布しているのではなく, 連続的な電荷密度の分布が存在している場合の, 静電エネルギーの表式を導出する.

イメージとしては, 前回はn個の電荷は砂粒のようなものとして考えたが, 今回は砂粒が集まって泥団子となったような, 電荷の塊として考える.

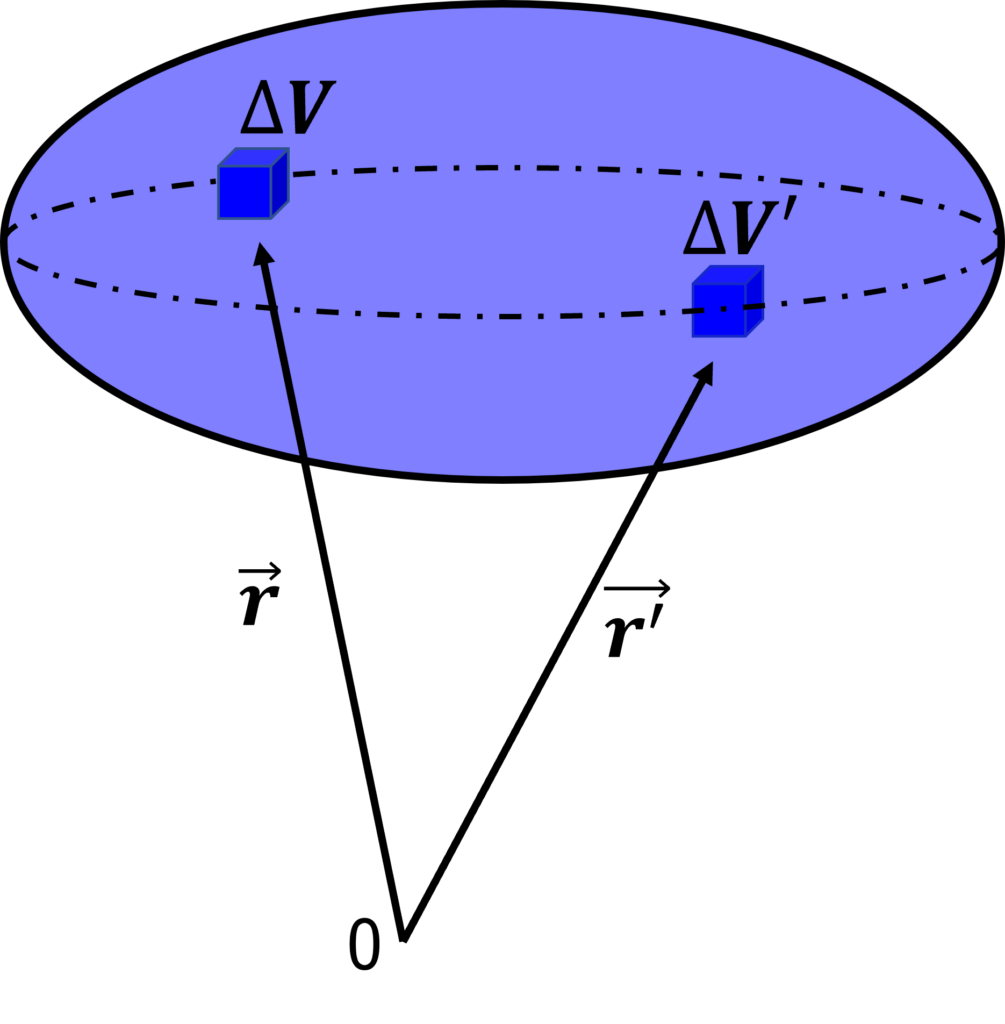
電荷の分布している領域を体積\(\Delta V\)の微小領域に分割し, それらの中の電荷をそれぞれ点電荷とみなし,

前回の記事で導いた関係

$$U = \frac{1}{8\pi\varepsilon_0}\displaystyle \sum_{i \ne j}^{n}\sum_{j \ne i}^{n}\frac{q_iq_j}{|\mathbf{r}_i – \mathbf{r}_j|}$$

を適用する. すなわち, 場所に依存した電荷密度\(\rho (\mathbf{r})\)の分布が存在する場合に置き換えて考える. 位置\({\mathbf{r}}\)にある体積\(\Delta V\)の微小空間には, \(\rho (\mathbf{r})\Delta V\)だけの電荷が存在する. したがって, 上の関係における\(\mathbf{r}_i\)を\(\mathbf{r}\)に, \(\mathbf{r}_j\)を\(\mathbf{r}’\)と置き換えることにより

$$U = \frac{1}{8\pi\varepsilon_0}\displaystyle \sum_{\mathbf{r}}\sum_{\mathbf{r}’}\frac{\left\{\rho (\mathbf{r})\Delta V\right\}\left\{\rho (\mathbf{r}’)\Delta V’\right\}}{|\mathbf{r} – \mathbf{r}’|}$$

\(\Delta V, \Delta V’ \ \rightarrow \ dV, dV’\)の極限を取って, 和を積分形式に直せば, 静電エネルギーの一般形的な表現は, 次のように書ける.

$$U = \frac{1}{2}\int\int\frac{\rho (\mathbf{r})\rho (\mathbf{r}’)}{4\pi\varepsilon_0|\mathbf{r} – \mathbf{r}’|}\mathrm{d}V\mathrm{d}V’$$

※\(\int dV\)は\(\mathbf{r}\)についての体積積分, \(\int dV’\)は\(\mathbf{r}’\)についての体積積分を表す.

または, 前回の記事

で登場した, ポテンシャルを用いた表現

\begin{align*}
& U = \frac{1}{2}\displaystyle \sum_{i=1}^n q_i\phi ‘_i\\
& \phi ‘_i = \frac{1}{4\pi\varepsilon_0}\displaystyle \sum_{j \ne i}^{n}\frac{q_j}{|\mathbf{r}_i – \mathbf{r}_j|}
\end{align*}

を連続分布した電荷に適用し, 次のように表すこともできる.

\begin{align*}
& U = \frac{1}{2}\int \rho (\mathbf{r})\rho (\mathbf{r}’)\mathrm{d}V\\
& \phi (\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\int\frac{\rho (\mathbf{r}’)}{|\mathbf{r} – \mathbf{r}’|}\mathrm{d}V’
\end{align*}