半径\(R\)の無限に長い円筒の内部に電荷が一様な密度\(\rho\)で分布しているとき, 中心軸方向の単位長さあたりに蓄えられる静電エネルギーを求めよ.
[解]
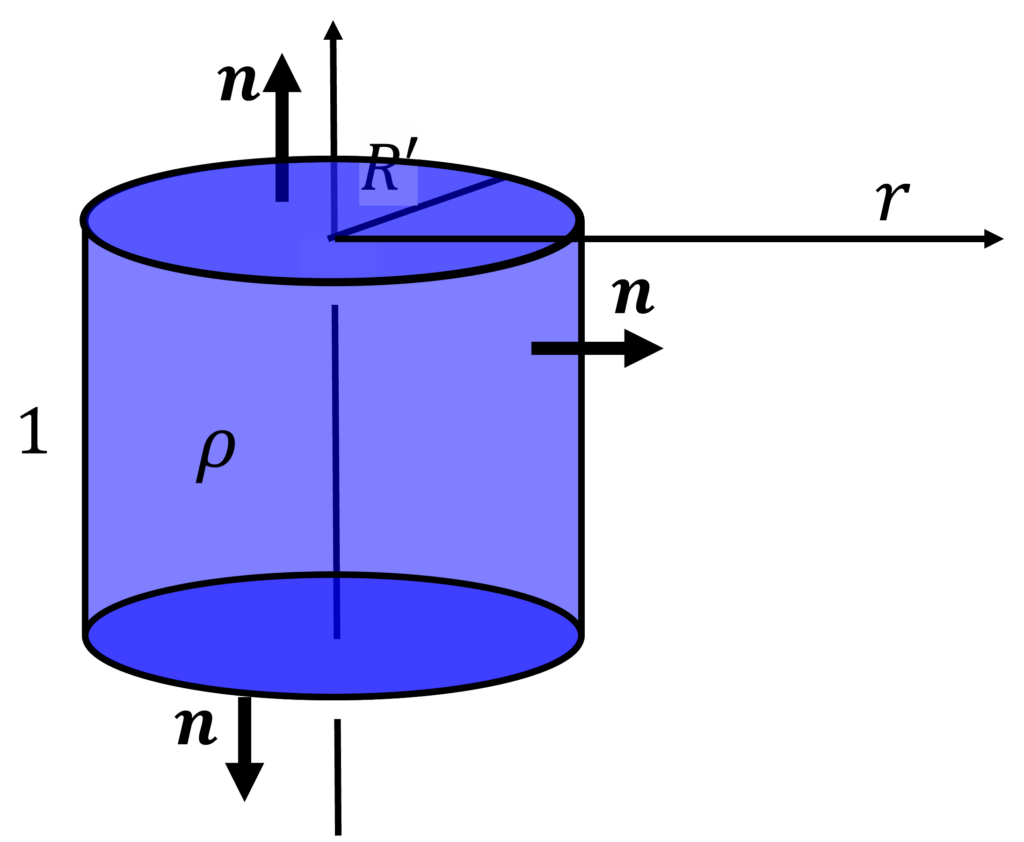
電荷が密度\(\rho\)で一様分布する円筒の半径を\(R’ (<R)\)とすると, 中心軸からの距離\(r (<R’)\)に生じる電場\(E(r)\)は, ガウスの法則により
\begin{align*}
\int \mathbf{E}\cdot \mathbf{n} dS &= 2\pi r \cdot 1 \times E(r) \\
&= \frac{\pi R’^2 \rho}{\varepsilon_0}
\end{align*}
が成り立つ. よって, 中心軸からの距離の関数として, 電場が得られる.
$$E(r) = \frac{\rho R’^2}{2\varepsilon_0}\frac{1}{r}$$
ここで, \(r = R\)での電位を基準とすると, \(r = R’\)での電位は,
\begin{align*}
\phi (R’) &= -\int_R^{R’} E(r)dr\\
&= \frac{\rho R’^2}{2\varepsilon_0}\left[-\mathrm{log}log r\right]_R^{R’}\\
&= \frac{\rho R^2}{2\varepsilon_0}\mathrm{log}log\frac{R}{R’}
\end{align*}
ここから, 長さ1, 半径\(R’\)の円筒面に厚み\(\Delta R\)の電荷殻を積み重ねることを考える. 無限遠から, 次式の電荷量(電荷密度×体積)
$$\Delta Q = \rho 2\pi R’\Delta R’$$
を運ぶ. 下図のようなイメージである.
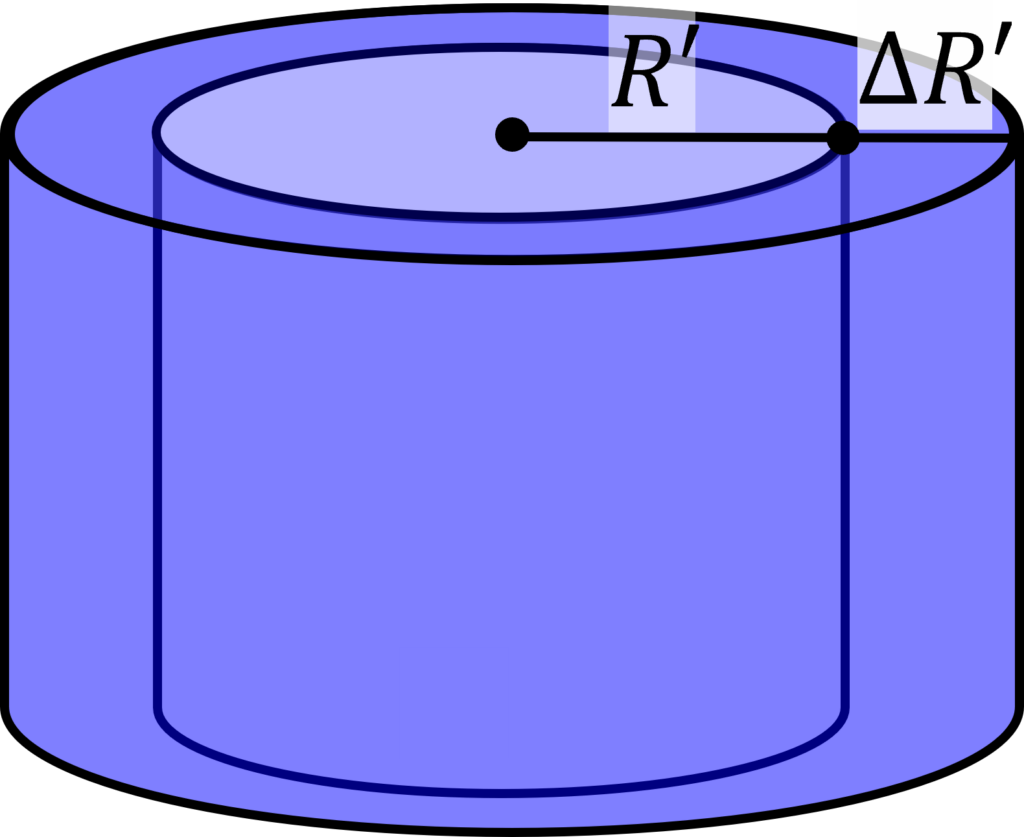
このように, 殻を形成するために, 電荷を無限遠から運んでくるために要する仕事は,
\begin{align*}
\Delta W &= \Delta Q \phi (R’) \\
&= \frac{\rho^2 \pi R’^3}{\varepsilon_0}\mathrm{log}\frac{R}{R’}\Delta R’
\end{align*}
\(\Delta R’ \rightarrow 0\)の極限をとり, \(R’\)について, \(R’ = 0\)から\(R’ = R\)まで積分を行うと, 所望の静電エネルギーを求めることができる.
\begin{align*}
U &= \frac{\rho^2 \pi}{\varepsilon_0}\int_0^R\left(R’^3\mathrm{log}R – R’^3\mathrm{log}R’3\right)\\
&= \frac{\rho^2 \pi}{\varepsilon_0}\left\{\left[\frac{1}{4}R’^4\mathrm{log}R\right]_0^R-\left[\frac{1}{4}R’^4\mathrm{log}R’\right]_0^R + \int_0^R\frac{1}{4}R’^4\cdot\frac{1}{R’}dR’\right\}\\
&= \frac{\rho^2 \pi R^4}{16\varepsilon_0}
\end{align*}
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市



コメント