有限長さの直線上に分布した電荷の作る電場については,
で長々とした計算で求め, その極限状態として, 無限に長い直線の作る電場を導き出した.
しかし, ガウスの法則を利用すれば, 電荷分布に空間的な対称性がある場合, 簡単に電場を求めることができる.
無限に長い直線上に一様な線密度\(\lambda\)で電荷が分布しているとき, ガウスの法則を用いて, 生じる電場を求めよ.
[解]
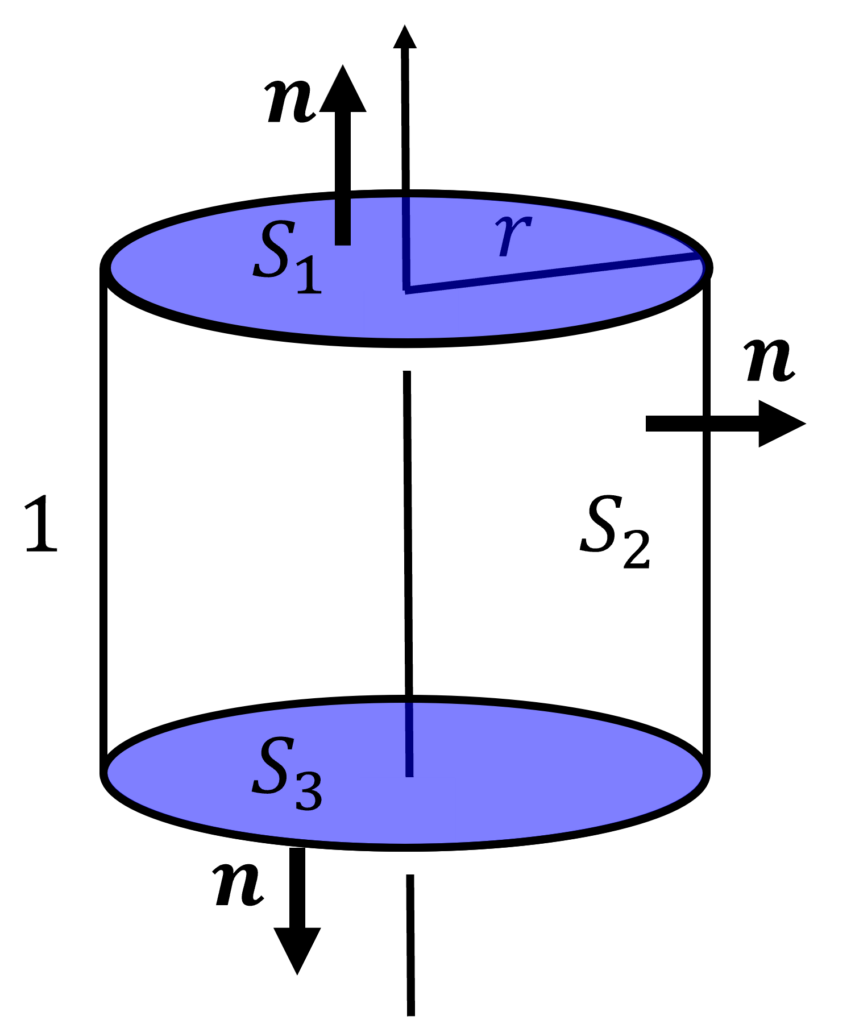
ガウスの法則は, 任意の閉曲面に対して成り立つので, 単位長さで半径\(r\)の円筒を考え, その中心軸を電荷の分布する直線に一致させる. 円筒表面Sでの電場を求め, \(r \)を任意の値とする事で, 任意の場所の電場を表すことができる.
上記の状況では, 円筒面上の電場が軸対称となる. ここで, 下図のように, あらゆる場所において, 上下の対称的な位置にある同サイズの微小部分からの電場の寄与について考える. すると, 直線と平行な方向の成分は打ち消し合い, 直線と垂直な方向の成分だけが残る.
したがって, 電場は円筒の側面と垂直に交わり, 底面とは平行なので, ガウスの法則により,
\begin{align*}
\int_S\mathbf{E}\cdot\mathbf{n}\mathrm{d}S &= \int_{S1}\mathbf{E}(r)\cdot\mathbf{n}\mathrm{d}S\\
& \ + \ \int_{S2}\mathbf{E}(r)\cdot\mathbf{n}\mathrm{d}S \\
& \ + \ \int_{S3}\mathbf{E}(r)\cdot\mathbf{n}\mathrm{d}S \\
&= 0 + \int_{S2}\mathbf{E}(r)\cdot\mathbf{n}\mathrm{d}S + 0\\
&= E(r)\cdot 2\pi r\cdot 1= \frac{1}{\varepsilon_0}(\lambda\cdot 1)
\end{align*}
最初の等式では, \(S_1, S_2\)に関する面積分が0となる. 上でも述べたが, 電場には無限長の直線と垂直な成分しかなく, 円筒の底面と電場の内積は0になるためである.
そして, 最後の等式にはガウスの法則を利用した. また, 直線上において, 単位長さあたりに含まれる電荷は\(\lambda\cdot 1\)であることを用いた. あえて1を省略せず書いたのは, 1という単位長さを表現したためである.
以上より, 電場は次のようになる.
$$E(r) = \frac{\lambda}{2\pi\varepsilon_0 r}$$
直線からの距離の関数として, 電場が求まった. 対称性とガウスの法則を用いたことで, 微小部分から受けるクーロン力の積分を計算するより, ずっと楽に求めることができた.
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市著




コメント