1. 電場と電位の関係
まず, 電場\(\mathbf{E}(\mathbf{r})\)(ベクトル関数)と電位\(\phi(\mathbf{r})\)(スカラー関数)の関係式は,
$$\mathbf{E}(\mathbf{r}) = -\nabla\phi(\mathbf{r}) \ …(1)$$
である. 電場は, 電荷働く力の大きさと方向を示すベクトルである. 一方, 電位とは, 座標\(\mathbf{r}\)ごとに与えられる, 山の高さのようなものである. 式(1)は, 電位という山の勾配(にマイナスをかけたもの)が, 電場ベクトルであるという関係式である.
要は, 電位という山が与えられたとき, ある地点における山の傾き(の大きさと向きを表すベクトル)が, その場所における電場である.
ここで, 勾配と関数の関係を言語化すると, 次のように言うことができる.
勾配の定義
勾配(ベクトル)とは,「今居る地点から, 微小に動いたときに, 関数の値が一番増加する向き」と, 「その微小な動きに対する関数の値の増加量」を表す(ベクトル)量である。
座標\(\mathbf{r}\)の関数\(f(\mathbf{r})\)について, その勾配ベクトル\(\mathbf{G}\)は, 演算子\(\nabla = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z}\right)\)を用いて, 次のように表される.
\begin{align*}
\mathbf{G}(\mathbf{r}) &= \nabla f(\mathbf{r})\\
&= \left(\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial}{\partial z}\right)
\end{align*}
電場と電位の関係の場合, 次のように表現することができる.
電場ベクトルとは, 「今居る座標から, 微小に動いたときに, 関数\(\phi(\mathbf{r})\)の値が最も減少する向き」と, 「その微小な動きに対する関数の値の減少量」を表すベクトル量である.
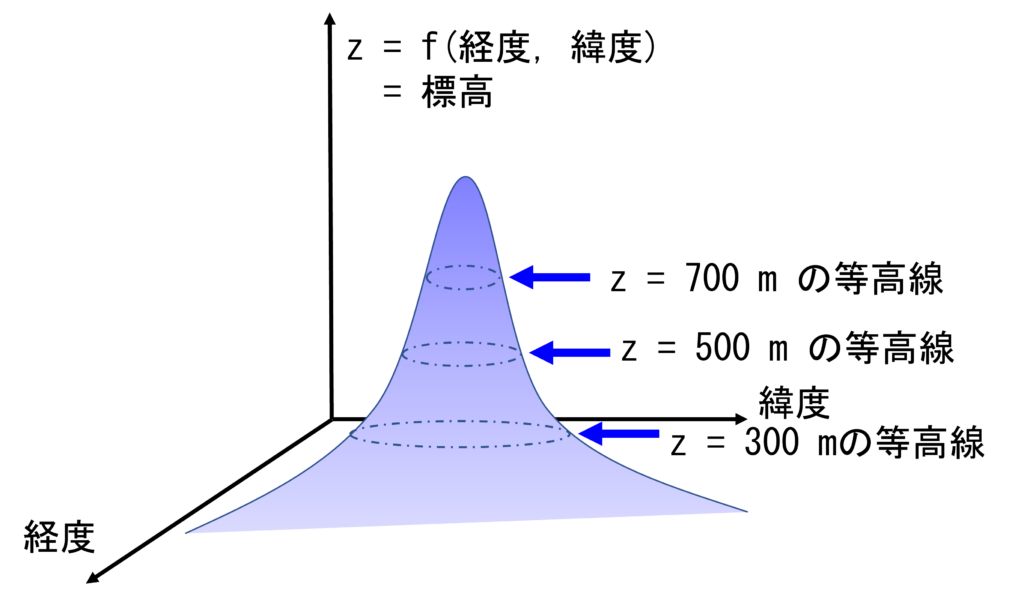
位置\(\mathbf{r}\)が2次元のベクトルであれば, 電位\(\phi(\mathbf{r})\)とは, 私たちの居る3次元空間における山の高さを示す「等高線」と全く同じようなイメージである. また, 等高線とは, 山の高さが同じ点を結んでできる“線”である.
一方, 位置\(\mathbf{r}\)が3次元のベクトルであれば, 電位\(\phi(\mathbf{r})\)は私たちの居る3次元空間における「見えない値の分布」となる. 難しいように思えるが, 例えば気温をイメージすればよい. 気温は, 緯度・経度・地表からの高度によって異なる値である. 一般に, 高度が上がるにつれて気温は低下し, 緯度が下がる(赤道方向に向かうほど)気温は高くなる. よって, 温度の等しい点を結んでいくと, 「等温面」を描くことができる.
例)二次元平面上の座標ごとに高さを持つ山
例)三次元空間内の座標ごとに(温度の)高さを持つ気温分布
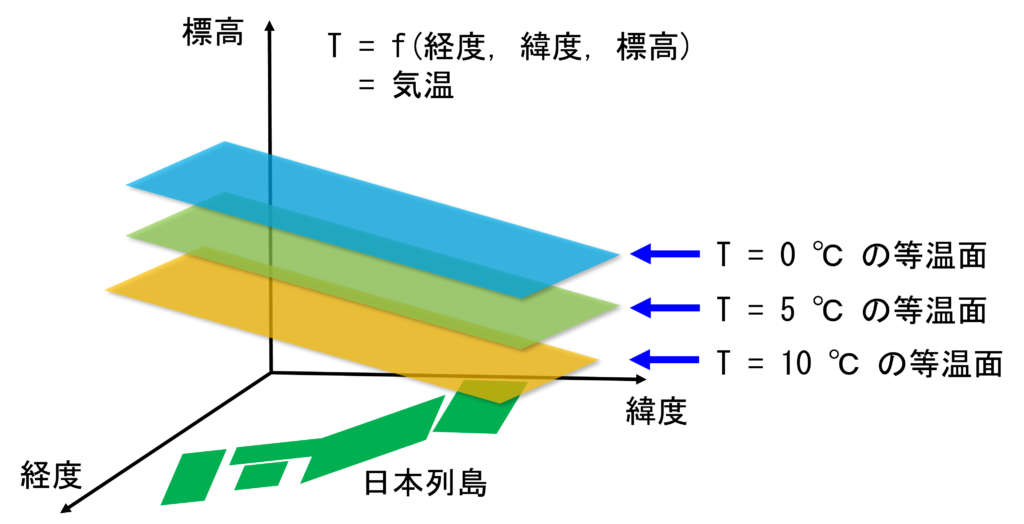
- 一般に, 気温は上空に行くほど低くなる.
- 九州上空(左の方)は, 日本の中では比較的低緯度な地域なので, 気温も比較的高い. すなわち, 北日本に比べると, 同じ標高における温度が高い.
- 北海道上空(右の方)は, 日本の中では比較的高緯度な地域なので, 気温も比較的低い. すなわち, 日本南部に比べると, 同じ標高における温度が低い.
こういった関係は, 等温面を考えると, 視覚的に分かりやすくなる.
3次元空間における等電位面とは、2次元空間における等高線のようなものであると解釈することができる. つまり, 2次元から3次元へと次元が増えたので, 線という1次元の図形も2次元の面へと次元が増えたのである.
2. 点電荷の作る電位をイメージする
点電荷が二次元空間内の原点に置かれているとき, 点\(\mathbf{r} = (x, y)\)における電位は,
$$\phi(\mathbf{r}) = \frac{q}{4\pi\varepsilon_0}\frac{1}{(x^2 + y^2)}$$
で表される. この時, 関係式(1)に基づいて, 点\(\mathbf{r} = (x, y)\)における電場を求めると,
\begin{align*}
\mathbf{E}(\mathbf{r}) &= \frac{q}{4\pi\varepsilon_0}\left(\frac{x}{r^3}, \frac{y}{r^3}\right)\\
&= \frac{q}{4\pi\varepsilon_0}\frac{\mathbf{r}}{|\mathbf{r}|^3}
\end{align*}
で与えられる. ここで, \(r = \sqrt{x^2 + y^2})は原点からの距離である. この結果の意味する物理的描像は,
- 電場の方向は\(\mathbf{r}\)と等しく, 放射状である.
- 電場の大きさは\(r^2\)に反比例するので, 原点から遠いほど, 電場は弱くなる.
ということである.
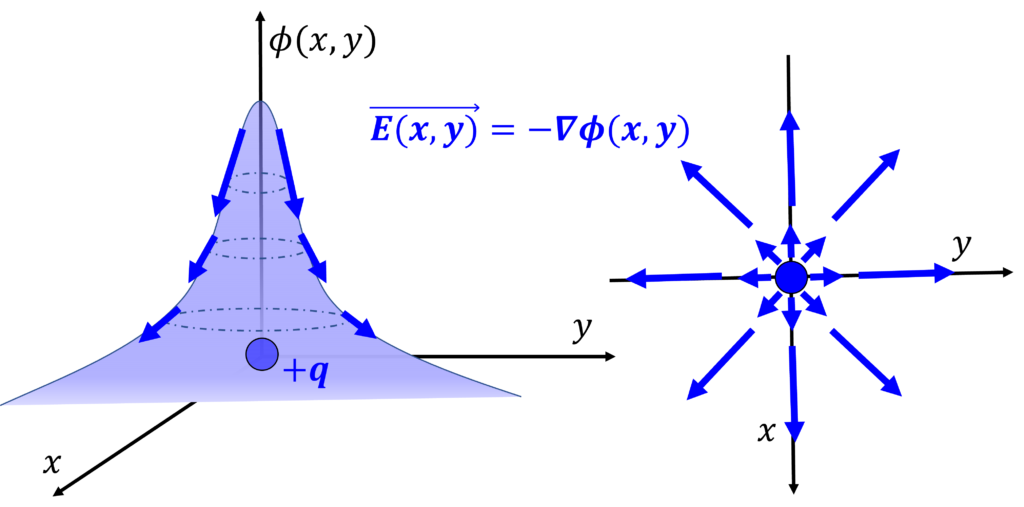
点電荷が三次元空間内の原点に置かれているときも, 全く同じ結果が得られる.
点\(\mathbf{r} = (x, y, z)\)における電位は,
$$\phi(\mathbf{r}) = \frac{q}{4\pi\varepsilon_0}\frac{1}{(x^2 + y^2 + z^2)}$$
で表される. この時, 関係式(1)に基づいて, 点\(\mathbf{r} = (x, y, z)\)における電場を求めると,
\begin{align*}
\mathbf{E}(\mathbf{r}) &= \frac{q}{4\pi\varepsilon_0}\left(\frac{x}{r^3}, \frac{y}{r^3}, \frac{z}{r^3}\right)\\
&= \frac{q}{4\pi\varepsilon_0}\frac{\mathbf{r}}{|\mathbf{r}|^3}
\end{align*}
3. 電場と等電位面の直交関係を示す
今回は, 電場ベクトルと等電位面が垂直であることを示したい.
まず, 等電位面上では, 位置\(\mathbf{r}\)が変わっても\(\phi(\mathbf{r})\)の値は一定である. ここで, 等電位面上における, 位置の微小変化を表す微小なベクトル\(\mathrm{d}\mathbf{r} = (\mathrm{d}x, \mathrm{d}y, \mathrm{d}z)\)を導入する. すると,
$$\phi(x, y, z) = \phi(x + \mathrm{d}x, y + \mathrm{d}y, y + \mathrm{d}y) .\ …(2)$$
が成り立つ. ここで, \(\mathrm{d}x, \mathrm{d}y, \mathrm{d}z\)は, 微小変位ベクトル\(\mathrm{d}\mathbf{r}\)の各成分を表す.
(2)を用いると, \(\phi\)の全微分は次のように表される.
\begin{align*}
\mathrm{d}\phi &= \phi(x + \mathrm{d}x, y + \mathrm{d}y, y + \mathrm{d}y) – \phi(x, y, z)\\
&= \frac{\partial \phi}{\partial x} + \frac{\partial \phi}{\partial y} + \frac{\partial \phi}{\partial z}\\
&= \nabla \phi \cdot \mathrm{d}\mathbf{r} = 0 \ …(3)
\end{align*}
ここで, \(\nabla \phi\)は関係式\(1)により, 電場ベクトルを与えるため, (3)から,
$$\mathbf{E}(\mathbf{r}) \cdot \mathrm{d}\mathbf{r} = 0$$
が得られる. 内積を取ると0となる2つベクトルは, 直交する.
ここで, 下図のように, \(\mathrm{d}\mathbf{r}\)は, 等電位面上における微小変位ベクトル, すなわち, 等電位面上の座標点\mathbf{r}における, 等電位面に平行なベクトルである.
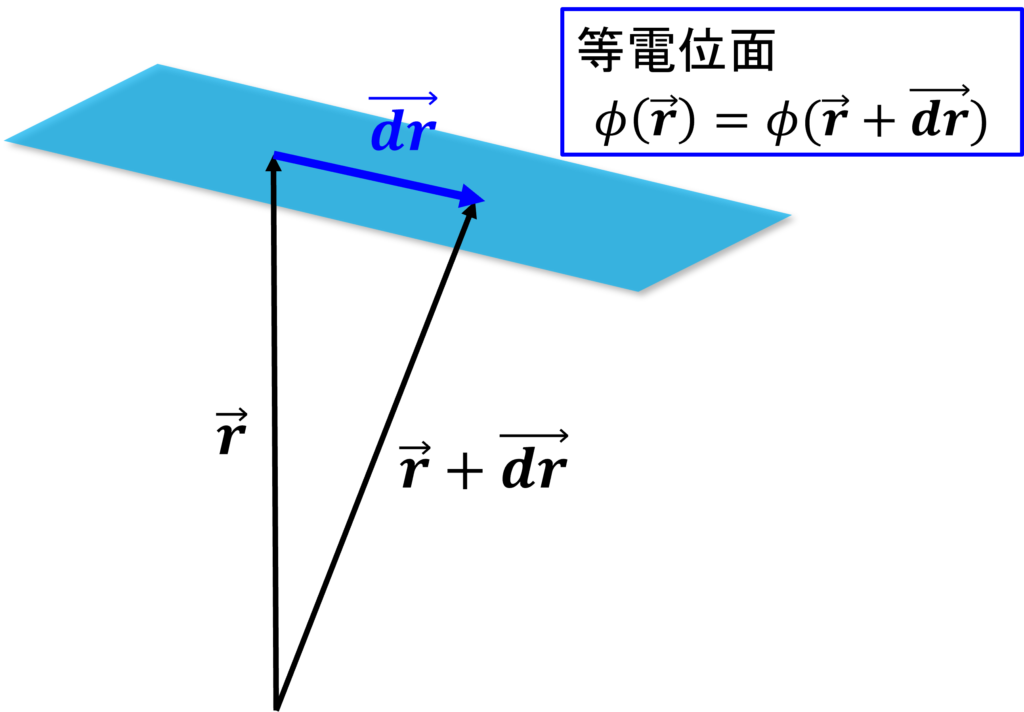
したがって, \(\mathbf{r}\)における電場\(\mathbf{E}(\mathbf{r})\)と等電位面上の任意の微小変位ベクトル\(\mathrm{d}\mathbf{r}\)が直交するため, 電場と等電位面は垂直である.
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市著



コメント