問題はこちら。院試対策・物理学の勉強にご利用ください。
また、誤植があればお問い合わせください。
問1:強制振動の微分方程式
1-1.
$$m\frac{d^2x}{dt^2} = – kx – b\frac{dx}{dt}$$
また、\(\sqrt{\frac{k}{m}} = \omega_0\)とおくと、運動方程式は次のように書ける。
$$\frac{d^2x}{dt^2} + 2\gamma\frac{dx}{dt} + \omega _0^2x = 0 …(1)$$
1-2.
\(x = e^{\lambda t}\)とおいて(1)に代入すると
$$(\lambda ^2 + 2\gamma\lambda + \omega _0^2)e^{\lambda t} = 0$$
すなわち、\(\lambda = – \gamma \pm \sqrt{\gamma ^2 – \omega _0^2}\)が得られる。
i)\(\gamma > \omega _0\)のとき
$$x(t) = e^{-\gamma t}(Ae^{\sqrt{\gamma ^2 – \omega _0^2}t} + Be^{-\sqrt{\gamma ^2 – \omega _0^2}t})$$
(A, Bは任意定数)これは、単調な減衰を表す。
ii)\(\gamma < \omega _0\)のとき
\(\lambda = \gamma \pm i\sqrt{\gamma ^2 – \omega _0^2}\)であるから
$$x(t) = e^{-\gamma t}(Asin\sqrt{\gamma ^2 – \omega _0^2}t + Bcos\sqrt{\gamma ^2 – \omega _0^2}t)$$
これは、振動減衰を表す。
iii)\(\gamma = \omega _0\)のとき
$$x(t) = (A + Bt)e^{-\lambda t}$$
これは、最も早い減衰(臨界減衰)を表す。
1-3.
$$m\frac{d^2x}{dt^2} + b\frac{dx}{dt}+ kx = F_0cos\omega t …(2)$$
1-4.
(2)を\(m\)で割って
$$\frac{d^2x}{dt^2} + 2\gamma\frac{dx}{dt}+ \omega _0^2x = \frac{F_0}{m}cos\omega t …(2)$$
ここで、拡張した解\(\tilde{x}(t)\)を上式の\(x\)に代入すると
$$(- \omega ^2 + 2i\gamma\omega + \omega _0^2)x_0e{i\omega t} = \frac{F_0}{m}e{i\omega t}$$
\begin{align*}
x_0 &= \frac{F_0}{m}\frac{1}{\omega _0^2 – \omega ^2 + 2i\gamma\omega}\\
&= \frac{F_0}{m}\frac{1}{(\omega _0^2 – \omega ^2)^2 + 4\gamma ^2\omega ^2}\left\{(\omega _0^2 – \omega ^2) – 2i\gamma\omega\right\}
\end{align*}
すなわち
\begin{align*}
x(t) &= R_e\tilde{x}(t)\\
&= R_e(x_0\cdot e{i\omega t})\\
&=\frac{F_0}{m}\frac{1}{(\omega _0^2 – \omega ^2)^2 + 4\gamma ^2\omega ^2}\cdot cos\omega t + \frac{F_0}{m}\frac{1}{(\omega _0^2 – \omega ^2)^2 + 4\gamma ^2\omega ^2}\cdot 2\gamma\omega sin\omega t
\end{align*}
1-5.
$$\left|\frac{x_0}{F_0}\right|^2 = \left|\frac{1}{m}\frac{1}{\omega _0^2 – \omega ^2 + 2i\gamma\omega}\right|^2 = \frac{1}{m^2}\frac{1}{(\omega _0^2 – \omega ^2)^2 + 4\gamma ^2\omega ^2}$$
ここで、上式の内
\begin{align*}
(\omega _0^2 – \omega ^2)^2 + 4\gamma ^2\omega ^2 &= \omega ^4 + (4\gamma ^2 – 2\omega _0^2)\omega ^2 + \omega _0^4\\
&= \omega ^4 -2(\omega _0^2 – 2\gamma ^2)\omega ^2 + \omega _0^4\\
&= {\omega ^2 – (\omega _0^2 – 2\gamma ^2)}^2 + (2\omega _0^2 – \gamma ^2 )\gamma ^2
\end{align*}
以上より、\(\omega ^2 = (\omega _0^2 – 2\gamma ^2)\)で\(\left|\frac{x_0}{F_0}\right|^2 \)は最大値を取ることが分かる。したがって、\(\left|\frac{x_0}{F_0}\right|^2\)の\(\omega\)依存性は下の図のようになる。
図(未挿入)
問2:回転座標系の運動方程式の導出
2-1.
\begin{align*}
|\Delta \mathbf{r}| &= R\omega \Delta t\\
&= |\mathbf{r}|sin\theta\cdot\omega\Delta t
\end{align*}
これをベクトルで表すと
$$\Delta \mathbf{r} = \mathbf{\omega}\times\mathbf{r}\Delta t$$
すなわち
$$\frac{d\mathbf{r}}{dt} = \mathbf{\omega}\mathbf{r}$$
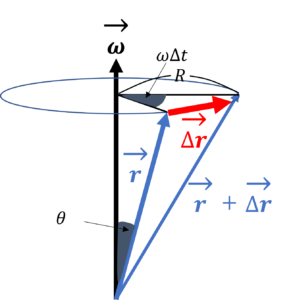
2-2.
非慣性系のベクトル基底ベクトルを\(\mathbf{e}’ = \mathbf{i}’ + \mathbf{j}’ + \mathbf{k}’\)とする。
\begin{align*}
\mathbf{r} &= x\mathbf{i} + y\mathbf{j} + z\mathbf{k}\\
&= x’\mathbf{i} + y’\mathbf{j} + z’\mathbf{k}
\end{align*}
が成り立つ。よって以下が成り立つ。
\begin{align*}
\frac{d\mathbf{r}}{dt} &= \dot{x}’\mathbf{i}’ + \dot{y}’\mathbf{j}’ + \dot{z}’\mathbf{k}’ + x’\dot{\mathbf{i}}’ + y’\dot{\mathbf{j}}’ +\dot{ z’\mathbf{k}}’\\
&= \frac{d\mathbf{r}*}{dt} + \mathbf{\omega}\times(x’\mathbf{i}’ + y’\mathbf{j}’ + z’\mathbf{k}’)\\
&= \frac{d\mathbf{r}*}{dt} + \mathbf{\omega}\times\mathbf{r}
\end{align*}
ここで、
を用いた。
2-3.
2-2より次式が成り立つ。
$$\frac{d\mathbf{r}}{dt} = \frac{d\mathbf{A}^*}{dt} + \mathbf{\omega}\times\mathbf{A} …(1)$$
まず、慣性系における運動方程式は
$$m\frac{d^2x}{dt^2} = \mathbf{F} …(2)$$
である。一方、(1)において、\(\mathbf{A} = \mathbf{v} = \frac{d\mathbf{r}}{dt}\)を代入すると
$$\frac{d\mathbf{v}}{dt} = \frac{d\mathbf{v}^*}{dt} + \mathbf{\omega}\times\mathbf{v} …(3)$$
となる。(3)に次の(4)を代入する。
$$\mathbf{v} = \frac{d\mathbf{r}}{dt} = \frac{d\mathbf{r}^*}{dt} + \mathbf{\omega}\times\mathbf{r} …(4)$$
\begin{align*}
\frac{d^2\mathbf{r}}{dt^2} &= \frac{d\mathbf{v}^*}{dt} + \mathbf{\omega}\times\mathbf{v}\\
&= \frac{d^*}{dt}\left(\frac{d\mathbf{r}^*}{dt} + \mathbf{\omega}\times\mathbf{r}\right) + \mathbf{\omega}\times\left(\frac{d\mathbf{r}^*}{dt} + \mathbf{\omega}\times\mathbf{r}\right)\\
&= \frac{d^{*2}r}{dt^2} + 2\mathbf{\omega}\times\frac{d\mathbf{r}^*}{dt} + \mathbf{\omega}\times(\mathbf{\omega}\times\mathbf{r}) …(5)
\end{align*}
(1), (5)より
$$\frac{1}{m}\mathbf{F} = \frac{d^{*2}\mathbf{r}}{dt^2} + 2\mathbf{\omega}\times\frac{d\mathbf{r}^*}{dt} + \mathbf{\omega}\times(\mathbf{\omega}\times\mathbf{r})$$
以上より、回転座標系における運動方程式は以下のようになる。
$$m\frac{d*^2\mathbf{r}}{dt^2}= \mathbf{F} – 2m\mathbf{\omega}\times\frac{d\mathbf{r}^*}{dt} – \mathbf{\omega}\times(\mathbf{\omega}\times\mathbf{r}) …(A)$$
2-4.
いま、\(\mathbf{\omega} = (0, 0, \omega)\)であるから、(A)の各成分ごとに次のようになる。
\begin{align*}
x成分:\frac{d^2x}{dt^2} = – \frac{g}{l}x + 2\omega\frac{dy}{dt} …(5)\\
y成分:\frac{d^2y}{dt^2} = – \frac{g}{l}y – 2\omega\frac{dx}{dt} …(6)
\end{align*}
(5), (6) より、\(\alpha = 2\omega, \beta = -2\omega\)
2-5.
\((5)\times y – (6)\times x\)を計算する。
$$y\frac{d^2x}{dt^2} = 2\omega y \frac{dy}{dt} + 2\omega x\frac{dx}{dt}$$
$$\frac{d}{dt}\left(y\frac{dx}{dt} – x\frac{dy}{dt}\right) = 2\omega\left\{\frac{d}{dt}\left(\frac{1}{2}y^2\right) + \frac{d}{dt}\left(\frac{1}{2}x^2\right)\right\}$$
両辺を\(t\)について積分して
$$\left(y\frac{dx}{dt} – x\frac{dy}{dt}\right) = \omega (x^2 + y^2) + C (Cは任意定数)…(7)$$
振動の軌道が\((x, y) = (0, 0)\)を通過するとすれば、\(C = 0\)である。
ここで、\(x = ucos\phi, y = usin\phi\)を(7)に代入すると
$$usin\phi(-usin\phi\cdot\dot{\phi}) – ucos\phi(ucos\phi\cdot\dot{\phi}) = \omega u^2(cos^2\phi + sin^2\phi)$$
$$u^2\dot{\phi} = – \omega u^2$$
$$\dot{\phi} = – \omega = \frac{d\phi}{dt}$$
これは、北極点において、振り子の振動面は「地球の自転の角速度と同じ大きさ・逆方向」の角速度をもって回転することを示している。



コメント