【解答・解説】平成２８年度北大理学院量子力学

問題はこちら。院試対策・物理学の勉強にご利用ください。
また、誤植があればお問い合わせください。

問１：１次元井戸型ポテンシャル

1-1.

２つの異なる波動関数$\psi_1(x) \neq \phi_2(x)$に対して、シュレーディンガー方程式

$$- \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi_1(x) + V(x)\phi_1(x) = E\phi_1(x) …(1)$$

$$- \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi_2(x) + V(x)\phi_2(x) = E\phi_2(x) …(2)$$

が成り立つと仮定する。$(1)\times\phi_2(x) – (2)\times\phi_1(x)$より

$$\psi_2\frac{d^2}{dx^2}\phi_1 – \phi_1\frac{d^2}{dx^2}\phi_2 = 0$$
$$\frac{d}{dx}\left(\phi_2\frac{d}{dx^2}\phi_1 – \phi_1\frac{d}{dx^2}\phi_2\right) = 0$$
$$\psi_2\frac{d}{dx^2}\phi_1 – \phi_1\frac{d}{dx^2}\phi_2 = C (Cは任意定数)$$
$x \rightarrow \pm \infty$で$\phi_1 = \phi_2 = 0$となることを課すと、$C = 0$。よって

$$\frac{1}{\phi_1}\frac{d}{dx}\phi_1 = \frac{1}{\phi_2}\frac{d}{dx}\phi_2$$
両辺を$x$について積分して
$$log\phi_1 = log\phi_2 + C_1$$
$$\phi_1 = C’\phi_2 (C_1, C’ は任意定数)$$

この結果は、仮定と矛盾する。したがって、縮退は生じない。

1-2.

$$- \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi(x) + V(x)\phi(x) = E\phi(x) …(3)$$

と、(3)において$x \rightarrow – x$とした（$V(-x) = V(x)$であることを利用）

$$- \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi(-x) + V(x)\phi(-x) = E\phi(-x) …(4)$$

に対して、

$$\phi(x) = C\phi(-x) (Cは任意定数)$$

が成り立つ。また

$$\phi(-x) = C\phi(x)$$

も成り立つので

$$\phi(x) = C^2\phi(x) \rightarrow C = \pm 1 $$

以上より、

$$
\phi(x) = \begin{cases}
\phi(-x) & (偶関数)\\
– \phi(-x) & (奇関数)
\end{cases}
$$

1-3.

$|x| > a$でのシュレーディンガー方程式は

$$- \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi(x) = E\phi(x)$$

これを解くと一般解は

$$\phi(x) = Asin\alpha x + Bcos\alpha x$$

となるが、$\phi(x)$は偶関数の場合を考えるので

$$\phi(x) = Acos\alpha x$$

$|x| < \alpha$でのシュレーディンガー方程式は

\begin{align*}
&- \frac{\hbar^2}{2m}\frac{d^2}{dx^2}\phi(x) + V_0\phi(x) = E\phi(x)\\
&\frac{d^2}{dx^2}\phi(x) -\frac{2m}{\hbar ^2}(V_0 – E)\phi(x) = 0
\end{align*}

これを$x \rightarrow \pm \infty$の境界条件の下で解くと
$x \rightarrow \pm \infty$では波動関数$\phi(x)$は発散しないため

\[
\phi(x) =
\begin{cases}
Ce^{\beta x} & (x < -a)\\
Ce^{-\beta x} & (x > a)
\end{cases}
\]

となる。以上のA, Cは任意定数である。

また、$x = a$での境界条件として、$\phi(x), \ \frac{d\phi(x)}{dx}$が連続であることを用いると

\begin{align*}
&Acos\alpha a = Ce^{-\beta a} \ …[1]\\
&-\alpha Asin\alpha a = -\beta Ce^{-\beta a} \ …[2]
\end{align*}

が得られる。$[2]/[1]$を計算すると

$$\alpha tan\alpha a = \beta \ …[3]$$

が得られる。

1-4.

[3]の両辺に$a$をかければ

$$\eta = \xi tan\xi \ …[4]$$

が得られる。また、

$$\eta ^2 + \xi ^2 = a^2(\alpha ^2 + \beta ^2) = \frac{2mV_0}{\hbar ^2}a^2 \ …[5]$$

の関係がある。よって、[4], [5]をグラフに表すと以下のようになる。

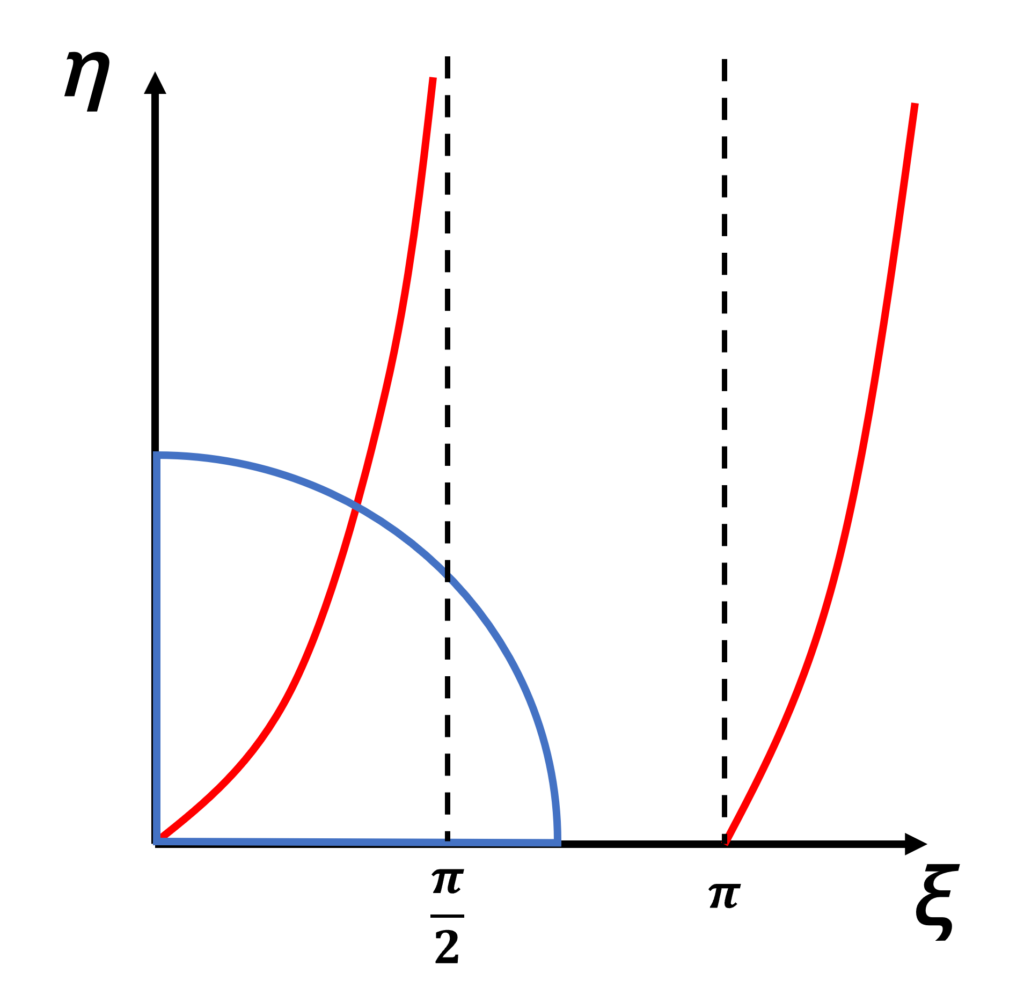
ここで、赤い曲線は[4]を示している。また、青い曲線は[5]の関係式を示しており、半径$\sqrt{\frac{2mV_0}{\hbar ^2}}a$の円である。

よって、エネルギー固有状態が唯一つになるための条件は、$\sqrt{\frac{2mV_0}{\hbar ^2}}a < \pi$である。

1-5.

$\frac{V_0 ma^2}{\hbar ^2} << 1$であるから、[5]より$\xi << 1$であることも明らかである。よって、[4]は

$$\eta \neq \xi\cdot\xi = \xi ^2$$

と近似することができる。これを[5]に代入すると、

$$\xi ^4 + \xi ^2 = \frac{2mV_0}{\hbar ^2}a^2$$

という$\xi$の４次方程式が得られる。これを解けば、

$$E = \frac{\hbar ^2}{4ma^2}\left(-1 + \sqrt{1 + \frac{8mV_0}{\hbar ^2}a^2}\right)$$

が得られる。ここで、求めた$E$に含まれる平方根の部分は

\begin{align*}
\sqrt{1 + \frac{8mV_0}{\hbar ^2}a^2} &\neq (1 + 8\lambda)^{\frac{1}{2}}\\
&= 1 + 4\lambda -8\lambda ^2
\end{align*}

のように展開することができる。すなわち

$$E \neq \frac{\hbar ^2}{ma^2}(\lambda – 2\lambda)$$

と書くことができる。

問２：電気双極子モーメントの摂動論

2-1.

\begin{align*}
[\mathbf{L}^2, L_z] &= [L_x^2 + L_y^2 + L_z^2, L_z]\\
&=L_x[L_x,L_z]+[L_x,L_z]L_x + L_y[L_y,L_z] + [L_y,L_z]L_y\\
&=L_x(-i\hbar L_y) + (i\hbar L_y)L_x + L_y(i\hbar L_x) + (i\hbar L_x)L_y\\
&= 0
\end{align*}

よって、$\mathbf{L}^2, \ L_z$は同時対角化可能である。

また、

$$[H_0, L_z] = \frac{1}{2I}[\mathbf{L}^2, L_z] = 0$$

なので、$H_0, \ L_z$は同時対角化可能である。

$$[\mathbf{L}^2, H_0] = \frac{1}{2I}[\mathbf{L}^2, \ \mathbf{L}^2] = 0$$

なので、$\mathbf{L}^2, \ H_0$は同時対角化可能である。

2-2.

\begin{align*}
H_1 &= – p\varepsilon cos\theta\\
&= – p\varepsilon\frac{z}{r} \propto z
\end{align*}

ここで、$L_z = xp_y – y_px$であり、これに$z$が含まれていないことから$L_z, \ H_1$は同時対角化可能である。
$|l, m\rangle$は$L_z$の固有ベクトルである。$L_z, \ H_1$は同時対角化可能であることより、$|l, m\rangle$は$H_1$の固有ベクトルでもある。よって、$m’ = m$を満たす必要がある。

2-3.

$$|\phi _n\rangle = \displaystyle\sum_{m=0}^{\infty}C_{nm}|\phi_m^{(0)}\rangle$$

と展開する。$C_{nm} = C_{nm}^{(0)} + \lambda C_{nm}^{(1)}+ O(\lambda ^2)$とする。ここで、シュレーディンガー方程式より

$$H|\phi _n\rangle = E_n|\phi _n\rangle $$

であるから、

\begin{align*}
(H_0 + \lambda H_1)|\phi _n\rangle &= (H_0 + \lambda H_1)\displaystyle\sum_{m=0}^{\infty}C_{nm}|\phi_m^{(0)}\rangle\\
&= \displaystyle\sum_{m=0}^{\infty}C_{nm}E_{m}^{(0)}|\phi_m^{(0)}\rangle\\
& \ + \lambda\displaystyle\sum_{m=0}^{\infty}C_{nm}H_1|\phi_m^{(0)}\rangle\\
&= \displaystyle\sum_{m=0}^{\infty}C_{nm}E_n|\phi_m^{(0)}\rangle
\end{align*}

のように式変形ができる。最後の２つの辺に対して、左から$\langle \phi_k^{0}|$をかけると

\begin{align*}
&\displaystyle\sum_{m=0}^{\infty}C_{nm}E_m^{(0)}\delta_{km} + \lambda\displaystyle\sum_{m=0}^{\infty}\langle\psi_k^{(0)}|H_1|\psi_m^{(0)}\rangle C_{nm}\\
&= \displaystyle\sum_{m=0}^{\infty}C_{nm}E_n\delta_{km}\\
&C_{nk}(E_k^{(0)} – E_n) + \lambda\displaystyle\sum_{m=0}^{\infty}\langle\psi_k^{(0)}|H_1|\psi_m^{(0)}\rangle C_{nm} = 0
\end{align*}

ここで$C_{nm} = \delta_{nm}$とすると、上式は$\lambda$の２次以上の項を無視して

\begin{align*}
&(\delta_{nk} + \lambda C_{nk}^{(1)}){E_k^{(0)} – E_n^{(0)} – \lambda E_n^{(1)}}\\
& \ + \lambda\displaystyle\sum_{m=0}^{\infty}(\delta_{nm} + \lambda C_{nm}^{(1)})\langle\psi_k^{(0)}|H_1|\psi_m^{(0)}\rangle = 0
\end{align*}

$\lambda$の次数で整理すると

\begin{align*}
&\delta_{nk}(E_k^{(0)} – E_n^{(0)})\\
& + \lambda {C_{nk}^{(1)}(E_k^{(0)} – E_n^{(0)}) – E_n^{(1)}\delta_{nk} + \langle\psi_k^{(0)}|H_1|\psi_m^{(0)}\rangle} + O(\lambda ^2)\\
&= 0
\end{align*}

上式において、$\lambda$の１次について等式が成り立つ必要がある。よって

i)$k = n$の場合

$$E_n^{(1)} = \langle\psi_n^{(0)}|H_1|\psi_n^{(0)}\rangle $$

ii)$k \neq k$の場合

$$C_{nk}^{(1)} = \frac{\langle\psi_k^{(0)}|H_1|\psi_n^{(0)}\rangle}{E_n^{(0)} – E_k^{(0)}}$$

が成り立つ。したがって

\begin{align*}
|\phi_n\rangle &= \displaystyle\sum_{m=0}^{\infty}(\delta_{nm} + \lambda C_{nm}^{(1)})\langle\psi_k^{(0)}\\
&= |\phi_n^{(0)}\rangle + \lambda C_{nn}^{(1)}|\phi_n^{(0)}\rangle + \lambda\displaystyle\sum_{m=0}^{\infty}\lambda C_nm^{(1)}|\phi_m^{(0)}\rangle \\
&= |\phi_n^{(0)}\rangle + \lambda\displaystyle\sum_{m\neq n}^{\infty}\frac{\langle\psi_m^{(0)}|H_1|\psi_n^{(0)}\rangle}{E_n^{(0)} – E_m^{(0)}}|\psi_m^{(0)}\rangle
\end{align*}

上では、\(C_nn^{(1)}\}は任意の値をとるので、0とした。以上より

$$|\phi_n^{(1)}\rangle = \lambda\displaystyle\sum_{m\neq n}^{\infty}\frac{\langle\psi_m^{(0)}|H_1|\psi_n^{(0)}\rangle}{E_n^{(0)} – E_m^{(0)}}|\psi_m^{(0)}\rangle$$

2-4.

$$E_{lm}^{(1)} = \langle l,m|H_1|l, m\rangle$$

ここで、$l’ \neq l \pm 1$であるから

$$E_{lm}^{(1)} = 0$$

また、2-3の結果を用いると

\begin{align*}
E_{lm}^{(2)} &= \langle \psi_n^{(0)}|H_1|\psi_n^{(1)}\rangle\\
&= \langle \psi_n^{(0)}|H_1|\left(\displaystyle\sum_{k\neq n}^{\infty}\frac{\langle\psi_k^{(0)}|H_1|\psi_n^{(0)}\rangle}{E_n^{(0)} – E_k^{(0)}}|\psi_k^{(0)}\rangle\right)\\
&= \displaystyle\sum_{k\neq n}^{\infty}\frac{|\langle\psi_k^{(0)}|H_1|\psi_n^{(0)}\rangle|^2}{E_n^{(0)} – E_k^{(0)}}\\
&= \frac{|\langle l+1, m|H_1|l, m\rangle|^2}{E_{l,m}^{(0)} – E_{l+1,m}^{(0)}}\\
& \ +\frac{|\langle l-1, m|H_1|l, m\rangle|^2}{E_{l,m}^{(0)} – E_{l-1,m}^{(0)}}
\end{align*}

$E_{lm}^{(0)} = \frac{l(l + 1)\hbar ^2}{2I}$であるから

\begin{align*}
E_{lm}^{(2)} &= \frac{(p\varepsilon)^2|\langle l+1, m|cos\theta|l, m\rangle|^2}{\frac{l(l + 1)\hbar ^2}{2I} – \frac{(l + 1)(l + 2)\hbar ^2}{2I}}\\
& \ + \frac{(p\varepsilon)^2|\langle l-1, m|cos\theta|l, m\rangle|^2}{\frac{l(l + 1)\hbar ^2}{2I} – \frac{l(l – 1)\hbar ^2}{2I}}\\
\end{align*}

あとは、与えられた結果（問題文最後の式）を代入すればよい。