はじめに
2次元平面において、ある点の座標(x, y)が与えられたとします。
この点が、三角形・四角形・….・n角形といった、任意の多角形の領域の内側に存在するか、外側に存在するかを判定したいとき、どのように実装すれば良いでしょうか。
結論は
ベクトルの外積を利用する!
です。
ウッ(・ω・)と思った方は多いのではないでしょうか。ベクトルの外積なんて、高校数学では習いません。ベクトルの外積は、理系大学のベクトル解析や、力学を履修して初めて出てくる概念です。(後でベクトル解析の復習も兼ねて、初学者にもわかるように解説します)
それほど難しいの概念ではないので、ここで簡単に解説します。
1. ベクトル解析の復習:2次元ベクトルの外積
2次元ベクトル\(\mathbf{a} = (a_x, a_y), \ \mathbf{b} = (b_x, b_y) \)の外積の定義は、2つのベクトル\(\mathbf{a}, \mathbf{b}\)のなす角\(\theta\)を用いて
\begin{align*}
\mathbf{a} \times \mathbf{b} &= |\mathbf{a}|\cdot|\mathbf{b}|sin\theta\\
&= absin\theta\\
\mathbf{b} \times \mathbf{a} &= -\mathbf{a} \times \mathbf{b}
\end{align*}
です。また、外積は、ベクトルの成分を用いて、次のように表すこともできます。なお、上の\(\theta\)を用いた表記と同じ結果を与えます。
$$\mathbf{a} \times \mathbf{b} = a_xb_y-a_yb_x$$
なお、図でイメージすると分かりやすいのですが、ベクトルの外積は、2つのベクトルを辺とする平行四辺形の負号付き面積に等しいです。負号付き面積と言うのは、文字通り、面積に+-があるという意味です。
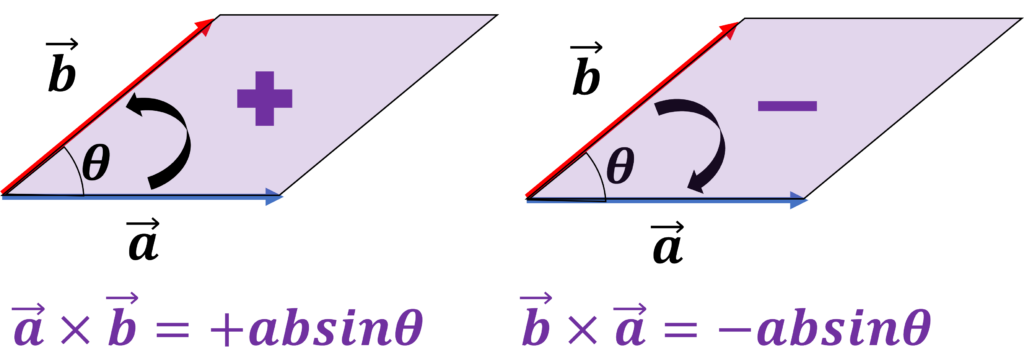
上図(左)のように、\(0 < \theta < 180\)の場合、\(\mathbf{a} \times \mathbf{b} \)は反時計回りの順番にかける場合、外積の値は正になります。
なお、数学や物理では、回転における反時計回りの方向(CCW:counter clock wise)を正に選ぶという慣習があります。
一方、上図(右)のように、時計回りの順番にかける場合、外積の値は負になります。
(番外編)3次元ベクトルの外積
3次元ベクトル
\[
\mathbf{a} = \left(
\begin{array}{c}
a_x \\
a_y \\
a_z
\end{array}
\right), \
\mathbf{b} = \left(
\begin{array}{c}
b_x \\
b_y \\
b_z
\end{array}
\right)
\]
の外積は
\[
\mathbf{a} \times \mathbf{b} = \left(
\begin{array}{c}
a_yb_z – a_zb_y \\
a_zb_x – a_xb_z \\
a_xb_y – a_yb_x
\end{array}
\right)
\]
となります。外積\(\mathbf{a} \times \mathbf{b}\)は、三次元空間上ではベクトルとなります。つまり、外積は、「平行四辺形の面積の大きさ」と、「ベクトルをかける順番で決まる向き」を持ったベクトルを返します。また、こちらの定義式がより一般的です。
下の図のように、反時計回りの順に外積を取ると正(上)方向のベクトルとなり、時計回りに外積を取ると負(下)方向のベクトルとなります。
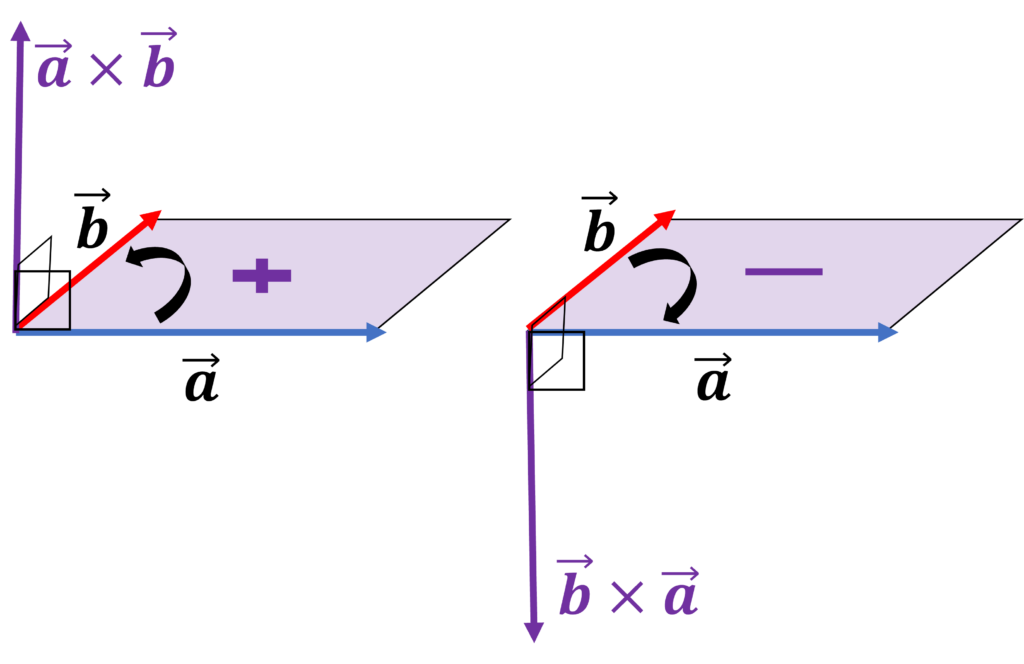
上で解説した2次元ベクトルの外積は、厳密には、x, y平面上の\(\mathbf{a} \times \mathbf{b}\)という、3次元ベクトルの外積のz成分を表しています。
なお、2次元ベクトルの場合に、計算結果がベクトルでない理由ですが、xy平面に平行なベクトル同士の外積では、外積ベクトルのx, y成分は0なので、省略しても構わないということです。
2. 外積を用いて、点の内外判定を行う
三角形領域内に点が存在する場合
ベクトルの外積の復習を終えたところで、三角形ABCが囲む領域内に、点Dが存在するか否かを判定する方法を考えていきましょう。まず、点Dが領域内にある場合を考えます。この時、ABベクトル・BCベクトル・CAベクトルを取ると、これは反時計回りに点をつないでいるような構図になります。
すると、
- ABベクトル => ADベクトルと反時計回りの順にかけた外積は正
- BCベクトル => BDベクトルと反時計回りの順にかけた外積は正
- CAベクトル => CDベクトルと反時計回りの順にかけた外積は正
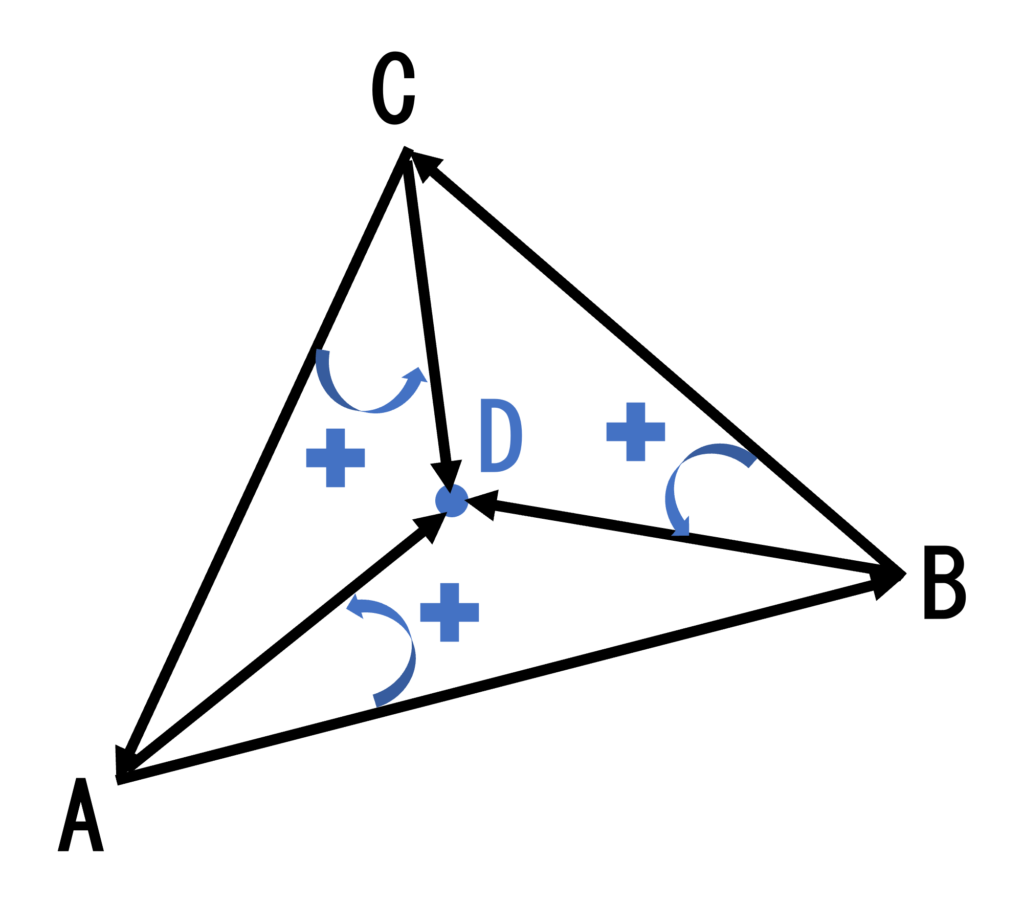
したがって、3つの外積はすべて正となります。したがって
点Dが対称の領域内に存在するとき、領域を成す各点(例えば点A)について、反時計回りにひとつ隣の点(B)に向かうベクトル(ABベクトル)と、各点から点Dに向かうベクトル(ADベクトル)の外積を求める。求めた外積の値が、各点について正であれば、点Dは領域内に存在する。
三角形領域外に点が存在する場合
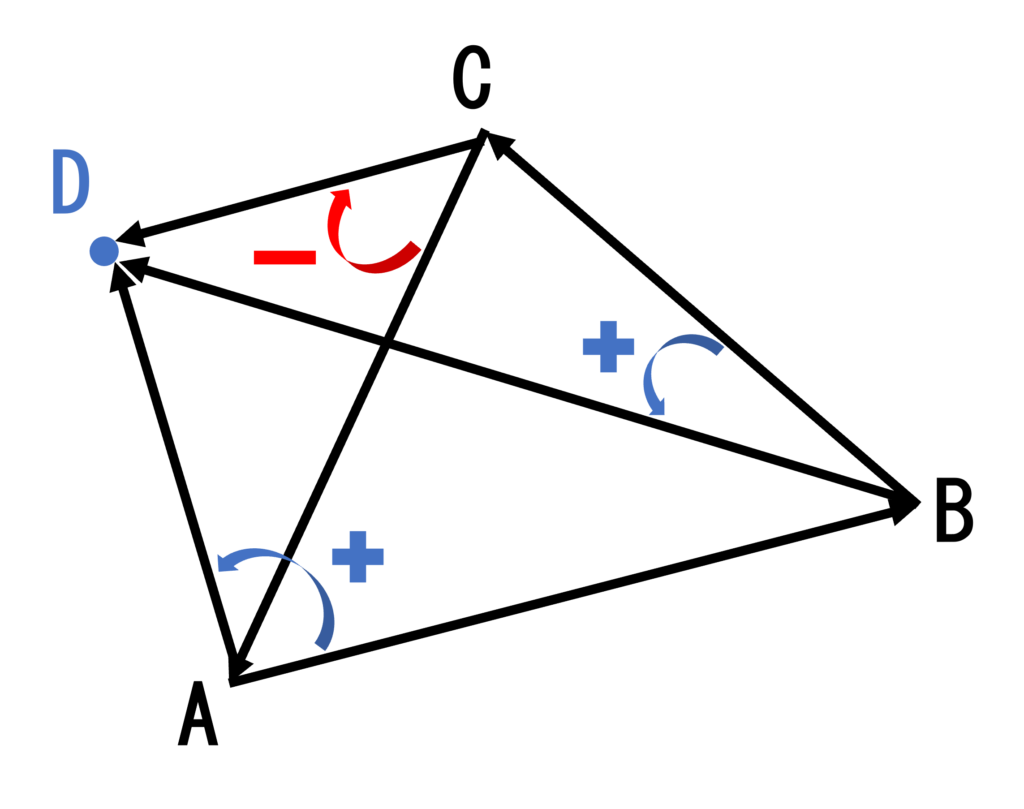
- ABベクトル => ADベクトルと反時計回りの順にかけた外積は正
- BCベクトル => BDベクトルと反時計回りの順にかけた外積は正
- CAベクトル => CDベクトルと時計回りの順にかけた外積は負
点Dが対称の領域内に存在するとき、領域を成す各点(例えば点A)について、反時計回りにひとつ隣の点(B)に向かうベクトル(ABベクトル)と、各点から点Dに向かうベクトル(ADベクトル)の外積を求める。各点について求めた外積の値が、1つでも負であれば、点Dは領域外に存在する。
3. Numpyを用いて内外判定を実装する(三角形ABCと点Dの場合)
では、点の内外判定の考え方を、Pythonのコードに落とし込んでいきます。
今回は、図のような三角形領域ABCに対し、点D1 : (2, 2), 点D2:(0, 3)が領域内に含まれるか、領域外に存在するかを判定します。領域を成す点の座標は、A:(1, 1), B:(4, 2), C:(2, 4)です。
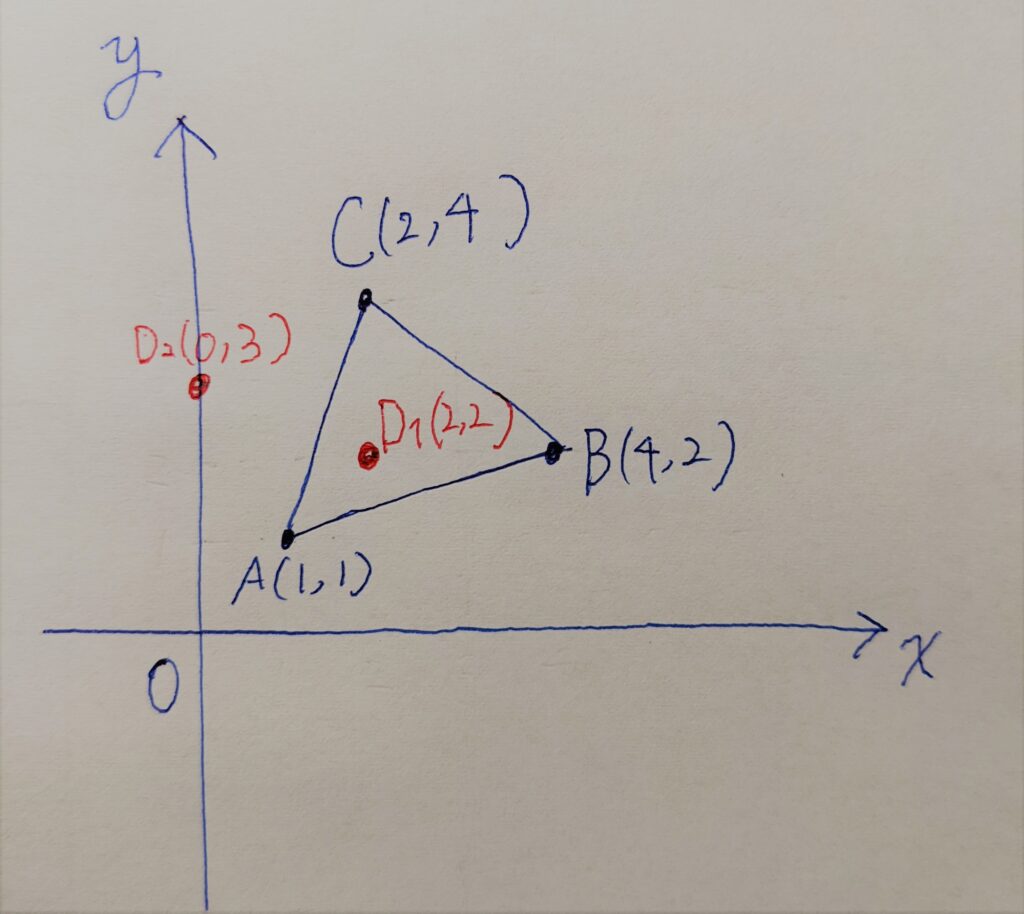
それでは、実装例を紹介します。注目すべきは以下の3点です。
- ベクトルは、numpy配列を用いて実装する。
- ベクトルの向きに注意する。(ABベクトルとは、Bベクトル-Aベクトルである)
- 三角形点を反時計回りに回る方向にベクトルを取った場合、AB, BC, CAベクトルのそれぞれに対して、AD, BD, CDベクトルと外積をとり、それら3つの符号が正だった場合、点Dが三角形の内部にあることを表す。
import numpy as np
# rectangle : 四角形
tri = [
[1, 1],
[4, 2],
[2, 4]
]
point_d1 = [2, 2] # 中にある点
point_d2 = [0, 3] # 外にある点
# 三角形abcに対し、点dの内外判定を行う関数
def in_triangle(triangle, point):
a = (triangle[0][0], triangle[0][1])
b = (triangle[1][0], triangle[1][1])
c = (triangle[2][0], triangle[2][1])
d = (point[0], point[1])
# 原点から各点へのベクトルを作る
vector_a = np.array(a)
vector_b = np.array(b)
vector_c = np.array(c)
vector_d = np.array(d)
# 点から点へのベクトルを求める
vector_ab = vector_b - vector_a #ABベクトル
vector_ad = vector_d - vector_a #ADベクトル
vector_bc = vector_c - vector_b
vector_bd = vector_d - vector_b
vector_ca = vector_a - vector_c
vector_cd = vector_d - vector_c
# 外積を求める
vector_cross_ab_ad = np.cross(vector_ab, vector_ad)
vector_cross_bc_bd = np.cross(vector_bc, vector_bd)
vector_cross_ca_cd = np.cross(vector_ca, vector_cd)
# 正だと点Dが三角形ABC中に存在し、負だと点Dは三角形ABC外に存在する
return vector_cross_ab_ad > 0 and vector_cross_bc_bd > 0 and vector_cross_ca_cd > 0
# 結果
print(in_triangle(tri, point_d1))
>> True # d1は領域内
print(in_triangle(tri, point_d2))
>> False # d2は領域外無事実装することができました!
4. 内外判定を実装する(四角形ABCDと点Eの場合)
「参考」の記事を基に、四角形領域バージョンも書いてみました。具体例として、四角形と、その内外にある2つの点を用意し、in_rect関数に代入して実行します。
import numpy as np
rect = [[1, 1],[3, 1],[3, 3],[1, 3]]
point_in = [2, 2]
point_out = [4, 5]
# ある点pointが、四角形(rectangle)に入っていたらTrue, 外にいたらFalseを返す
def in_rect(rect,target):
a = (rect[0][0], rect[0][1])
b = (rect[1][0], rect[1][1])
c = (rect[2][0], rect[2][1])
d = (rect[3][0], rect[3][1])
e = (target[0], target[1])
# 原点から点へのベクトルを求める
vector_a = np.array(a)
vector_b = np.array(b)
vector_c = np.array(c)
vector_d = np.array(d)
vector_e = np.array(e)
# 点から点へのベクトルを求める
vector_ab = vector_b - vector_a
vector_ae = vector_e - vector_a
vector_bc = vector_c - vector_b
vector_be = vector_e - vector_b
vector_cd = vector_d - vector_c
vector_ce = vector_e - vector_c
vector_da = vector_a - vector_d
vector_de = vector_e - vector_d
# 外積を求める
vector_cross_ab_ae = np.cross(vector_ab, vector_ae)
vector_cross_bc_be = np.cross(vector_bc, vector_be)
vector_cross_cd_ce = np.cross(vector_cd, vector_ce)
vector_cross_da_de = np.cross(vector_da, vector_de)
return vector_cross_ab_ae > 0 and vector_cross_bc_be > 0 and vector_cross_cd_ce > 0 and vector_cross_da_de > 0
print(in_rect(rect, point_in))
>> True # point_inは領域内
print(in_rect(rect, point_out))
>> False # point_outは領域外四角形でも上手く実装できました!
さいごに
今回は、最も簡単な多角形である、三角形について実装しましたが、四角形以上の多角形についても、簡単に実装することができます。nの大きなn角形の場合は、ループ処理を上手く利用する必要がありそうです。
先日、AtcoderのABC266で出会った問題(C – Convex Quadrilateral (atcoder.jp))では、点の内外判定を使用する必要がありました。(内容は、四角形の凹凸判定を行うというものだが、点の内外判定を応用することができる。)外積を使う場面は日常生活ではなかなかありませんが、今回の例は非常に実用的ですね。
参考:四角形の場合について解説されています。
https://yutako0217.hatenablog.com/entry/2018/05/23/070535
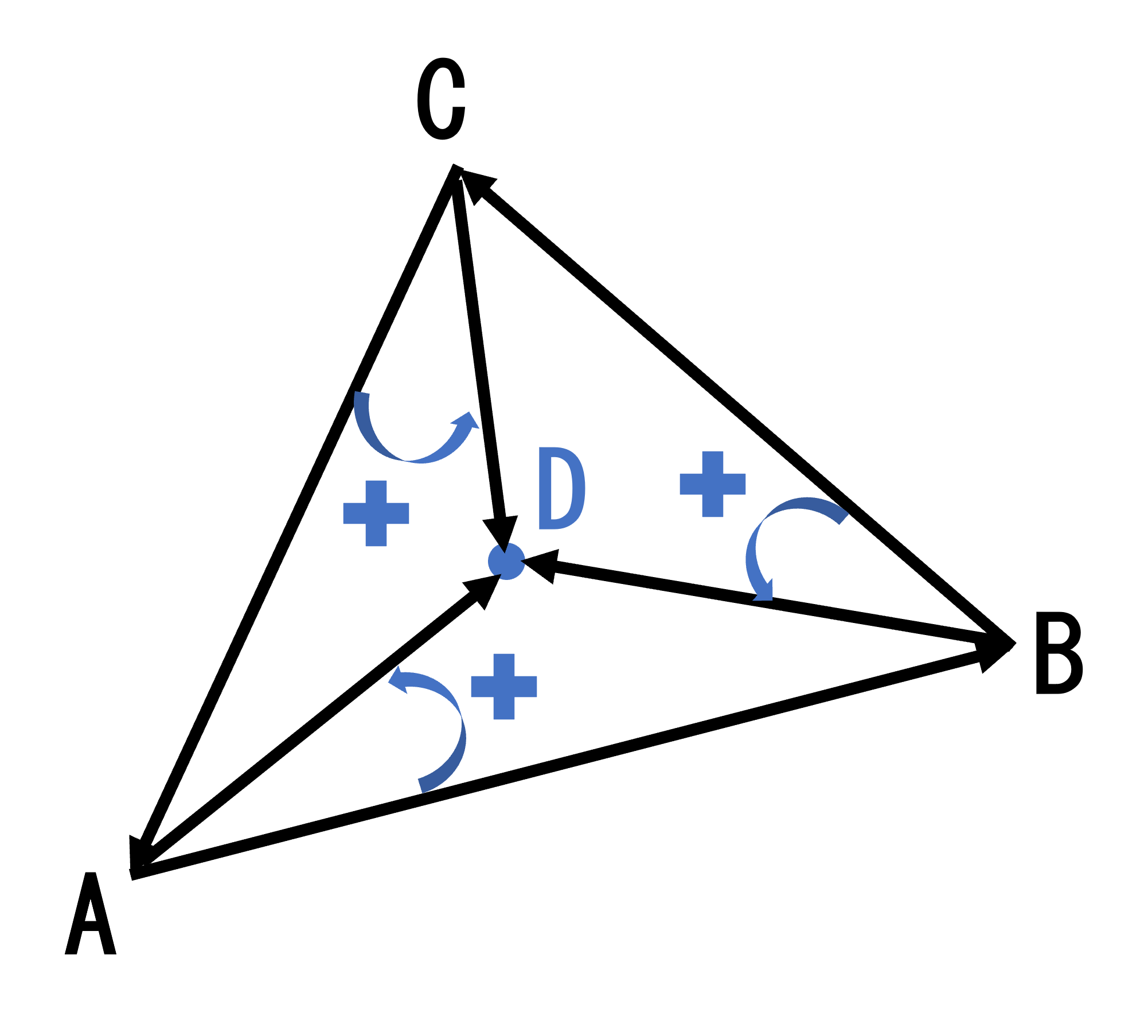


コメント