電気双極子を成す, 大きさの等しい, 逆符号の2つの電荷のペアがz軸上に置かれていることを考える.
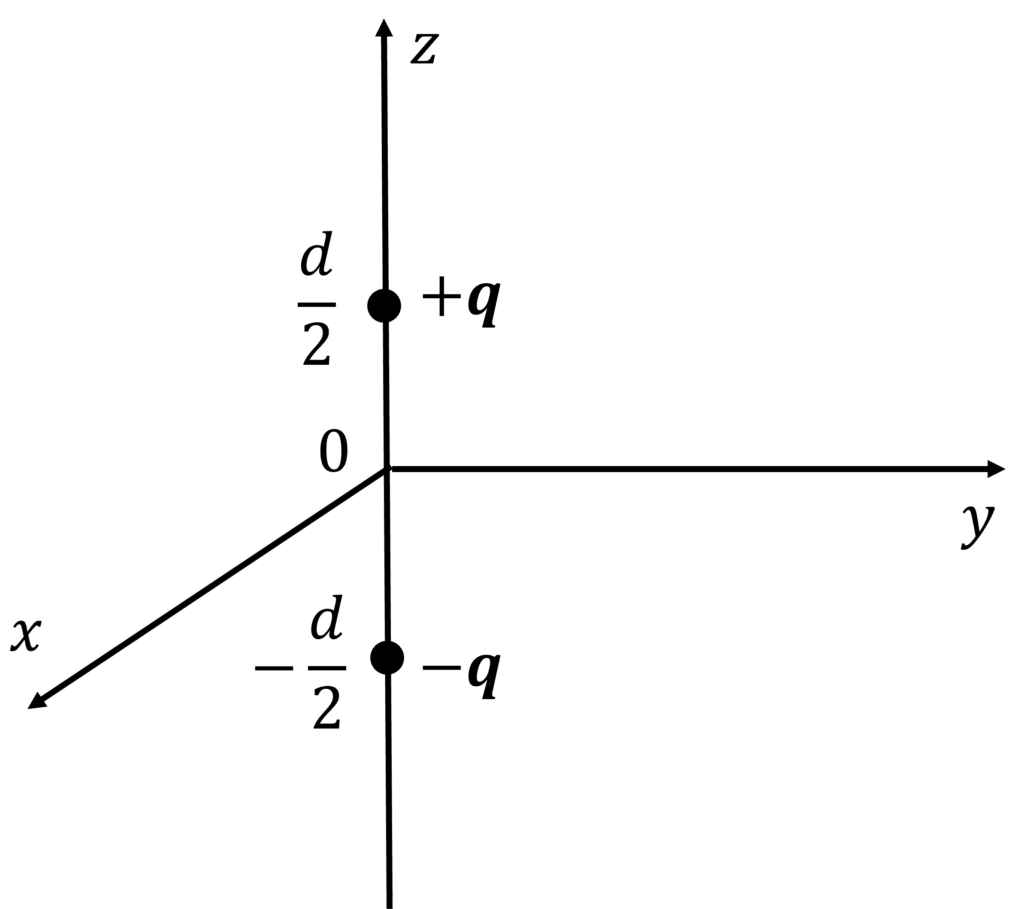
上図のように電荷を配置したとき, 点P(\(\mathbf{r} = (x, y, z)\))における電位\(\phi (\mathbf{r})\)は, \(+q\)による電位\(\frac{q}{4\pi\varepsilon_0}\frac{q}{r_1}\)と, \(-q\)による電位\(\frac{-q}{4\pi\varepsilon_0}\frac{1}{r_2}\)の和である.
ここで, 電位はx, y座標に依存しないので, 点Pを原点からの距離\(r\)と角度\(\theta\)によって指定することができる.

また, 下図のように\(\theta\)が鋭角の場合, 点Pが原点から十分離れている(\(d \ll r\)を満たす)と仮定すると,
\begin{align*}
r_1 \cong r – \frac{d}{2}\mathrm{cos}\theta\\
r_2 \cong r + \frac{d}{2}\mathrm{cos}\theta
\end{align*}
のように近似できることが分かる. この関係式の意味は, 点Pが原点から十分遠くにあれば, \(r\)と, \(r_1, r_2\)との長さの差は近似的に求まるということを表している.
ちなみに, \(\theta\)が鈍角でも\(r_1, r_2\)の大小関係が入れ替わるだけなので, 上記の関係式が成り立つ. \(\theta \rightarrow \theta + \frac{\pi}{2}\)としてみればすぐにわかる.

以上の議論をまとめると, 電気双極子による電位を次のように計算できる.
\begin{align*}
\phi (\mathbf{r}) &= \frac{q}{4\pi\varepsilon_0}\frac{q}{r_1} + \frac{-q}{4\pi\varepsilon_0}\frac{1}{r_2}\\
&= \frac{q}{4\pi\varepsilon_0}\left(\frac{r_2 – r_1}{r_1r_2}\right)\\
&\cong \frac{q}{4\pi\varepsilon_0}\frac{\left(r + \frac{d}{2}\mathrm{cos}\theta\right) – \left(r – \frac{d}{2}\mathrm{cos}\theta\right)}{\left(r – \frac{d}{2}\mathrm{cos}\theta\right)\left(r + \frac{d}{2}\mathrm{cos}\theta\right)}\\
&= \frac{q}{4\pi\varepsilon_0}\frac{d\mathrm{cos}\theta}{r^2 – \frac{d^4}{4}\mathrm{cos}^2\theta}\\
&\cong \frac{q}{4\pi\varepsilon_0}\frac{d\mathrm{cos}\theta}{r^2}\\
&= \frac{|\mathbf{p}|}{4\pi\varepsilon_0}\frac{|\mathbf{r}|\mathrm{cos}\theta}{r^3}
\end{align*}
1つめの近似では, 上記で図解した関係式を用いた. 2つめの近似では, \(r^2\)と比べて非常に小さい\(d^4\)は無視することとした. また, 最後の方では, 電気双極子モーメント\(\mathbf{p} = q\mathbf{d}\)を用いた. さらに
ベクトルの内積の定義
$$\mathbf{A}\cdot\mathbf{B} = |\mathbf{A}||\mathbf{B}|\mathrm{cos}\theta$$
を用いることで, 次の結果が得られる.
電気双極子モーメント\(\mathbf{p}\)による電位
$$\phi (\mathbf{r}) = \frac{1}{4\pi\varepsilon_0}\frac{\mathbf{p}\cdot\mathbf{r}}{r^3}$$
これは, デカルト座標を用いて得られる結果と一致する.



コメント