【正規分布】ガウスフィッティングの方法と積分強度・FWHMの誤差解析【Python】

1. 積分強度とその誤差を求めたい

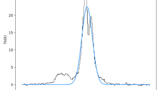
下図のような正規分布に従うデータがあるとします．黒い点はサンプル（実データ），青い曲線は，それをガウス関数$f(x) = A\mathrm{exp}\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$でフィッティングしたものです．

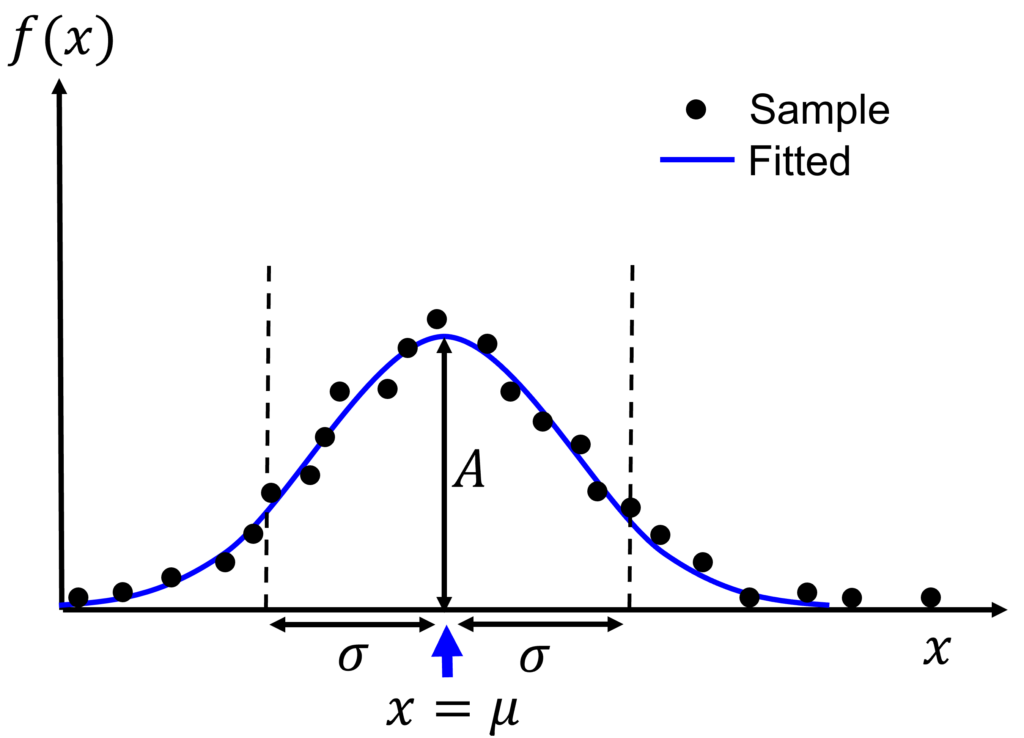
これについて，データの取りうる全区間における積分値，つまり下図の青い領域の面積は，重要な意味を持つことが多いです．例えば，横軸が年齢，縦軸がその年代の世界の人口の場合，青い領域の面積は「世界の総人口」を表します．また，物理学や化学の分野では，何らかの物体化から検出された光のスペクトルを扱う時，横軸に周波数，縦軸に光の強度をとります．そして，青い領域の面積を「積分強度」と呼びます（以下，全区間における積分値を積分強度と呼ぶ）．積分強度は，光を発する物質の量を見積もるのに使われたりと，重要な意味を持つ物理量です．

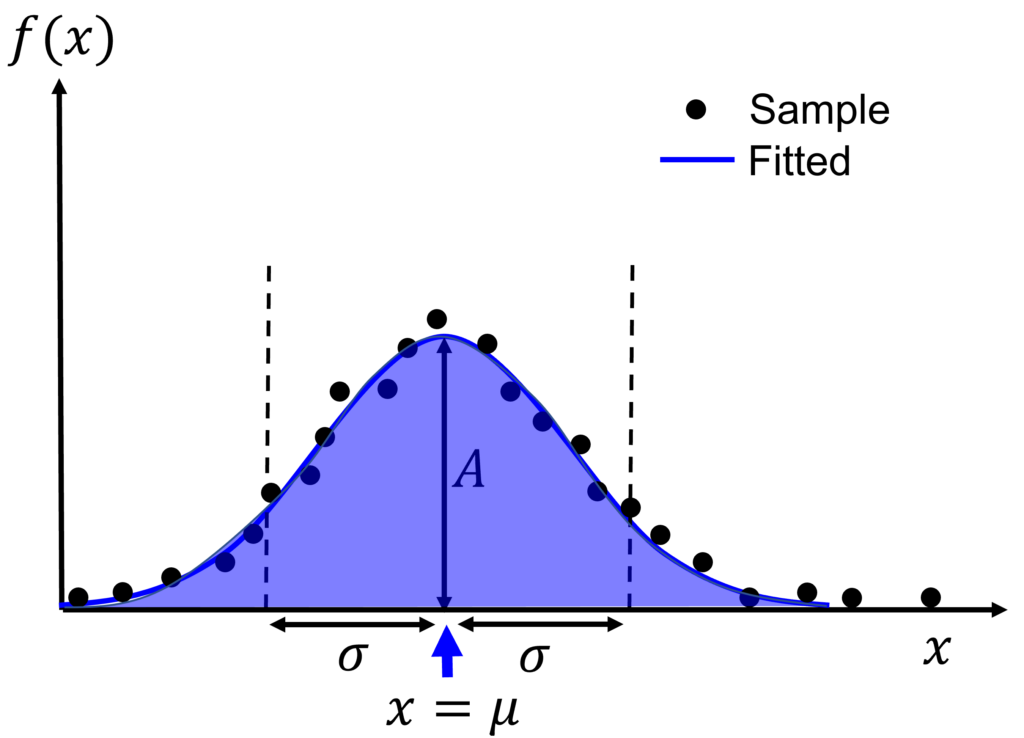
このように，科学全般において，正規分布に従うデータを解析し，その積分値（積分強度）を求めるという統計的な処理は重要です．また，その積分値の誤差も見積もる必要があります．本記事では，Pythonを用いてデータをガウス関数（正規分布）でフィッティングした後，積分強度および積分強度の誤差を求めるまでの方法を解説します．

2. ガウス積分の値とFWHM

ガウス関数
$$f(x) = A\mathrm{exp}\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$$

変数は$x$，パラメータはピーク値$A$，中央値$\mu$，標準偏差$\sigma$の３つとなります．確率密度関数は$A=\frac{1}{\sqrt{2\pi}\sigma}$の場合に相当します．確率密度関数は、全領域での積分値が１になるように$A$を規格化したものです．

ガウス関数の全区間における積分（ガウス積分）は，次の重要な性質を持ちます．

ガウス積分の公式
$$\int_{-\infty}^{\infty}e^{-x^2}dx = \sqrt{\pi}$$

ここで，ガウス積分の公式において，$x \rightarrow \frac{x-\mu}{\sqrt{2}\sigma}$と置き換えることにより，積分強度$I$を得ることができます．

積分強度
$$I = \int_{-\infty}^{\infty}A\mathrm{exp}\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)dx = A\sigma\sqrt{2\pi}$$

3. Pythonによるガウスフィッティング

任意の関数によるデータのフィッティングについては，こちらの記事で解説しています．

【曲線近似】Scipyのcurve_fitを用いて、任意の関数でカーブフィッティング（Python）

大学の研究などで、取得したデータを直線近似したり、非線形関数やガウス関数といった複雑な関数で近似する必要のある場面は多いと思います。そこで、機械学習ライブラリを使って、簡単に、しかも任意の関数に対してカーブフィッティング（曲線近似）を行い、パラメータの誤差まで算出できる便利な方法を紹介したいと思います。

上の記事と重複している内容もありますが，ガウス関数によるフィッティングや，フィッティング結果の扱について示します．

# ライブラリのインポート
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import numpy as np

# モデル関数の定義
def gauss_func(x,a,mu,sigma):
    """ガウシアン（正規分布）"""
    return a*np.exp(-(x-mu)**2/(2*sigma**2))

# フィッティングを行うための関数
def fit(func, x, param_init):
    """
    func:データxに近似したい任意の関数
    x:データ
    param_init:パラメータの初期値
    popｔ:最適化されたパラメータ
    pocv:パラメータの共分散
    """
    X = x[0]
    Y = x[1]
    popt,pocv=curve_fit(func, X, Y, p0=param_init)
    perr = np.sqrt(np.diag(pocv)) #対角成分が各パラメータの標準誤差に相当
    y=func(sample_x, *popt)
    return y, popt, perr

# パラメータの初期値の設定
param_init = [7, 2.5, 1]
# グラフ描画用のサンプルデータ
sample_x = np.arange(0, 5, 0.01)

# サンプルデータの用意
data_gauss_func = np.array([
        [0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5],
        [0, 0.5, 2.5, 4.5, 6, 7, 6.5, 4.5, 2.4, 0.5, 0],
                           ])

# フィッティングの実行
result = fit(gauss_func, data_gauss_func, param_init)
fig, ax = plt.subplots(1, 1, figsize=(6, 6))
ax.scatter(data_gauss_func[0], data_gauss_func[1])
ax.plot(sample_x, result[0])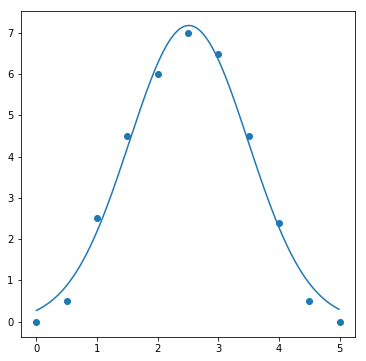

このように，データを上手くフィッチングすることができました．最後に，その結果を用いて，積分強度とFWHMという，重要な値を求める方法を解説します．

4. フィッティング結果から積分強度・FWHMとそれらの誤差を求める

まず，上のフィッティングの結果として，各パラメータの最適値$A, \mu, \sigma$と，標準誤差$\delta_A, \delta_{\mu}, \delta_{\sigma}$は次のように得られます．

\begin{align*}
\mathrm{result}[1] =[A, \mu, \sigma]\\
\mathrm{result}[2] = [\delta A, \delta {\mu}, \delta {\sigma}]
\end{align*}

A, mu, sigma = result[1]
d_A, d_mu, d_sigma = result[2]

では，FWHM（半値全幅）を求めます．FWHMは，ガウス関数$f(x)$に対して，最大値$A$の半分の値を与える$x$と，中央値$\mu$との差の絶対値です．そして，FWHMの最適値は次式のように与えられます．

$$\overline{\mathrm{FWHM}} = 2\sqrt{2\mathrm{ln}2}\sigma$$

よって，Python上でも，簡単な掛け算で求めることができます．

# fwhmの最適値
fwhm_0 = 2 * (2 * math.log(2)) ** 0.5 * sigma

また，$\mathrm{FWHM}$の誤差$\delta\mathrm{FWHM}$を含めると，$\mathrm{FWHM}$を次のように見積もることができます．

$$\mathrm{FWHM} = \overline{\mathrm{FWHM}} + \delta \mathrm{FWHM}$$

ここで，誤差解析における次の性質を用います．

任意の1次変数関数における誤差
$x$の測定誤差が$\delta x$の時，関数$f(x)$の誤差$\delta f$は次のようになる．
$$\delta f = \left| \frac{df}{dx} \right| \delta x$$

このとき，右辺2項目の標準誤差は，次のように求まります．

$$\delta \mathrm{FWHM} = 2\sqrt{2\mathrm{ln}2}\delta \sigma$$

# fwhmの誤差
d_fwhm_= 2 * (2 * math.log(2)) ** 0.5 * d_sigma

同様に積分強度が次のように書けるときを考えます．

$$I = \overline{I} + \delta I$$

積分強度の最適値は，ガウス積分の公式より$ \overline{I} = A\sigma\sqrt{2\pi}$と求まります．

# 積分強度の最適値
I_0 = A * sigma * (math.pi) ** 0.5

任意の多変数関数における誤差
$x, y, z, …$の測定誤差が$\delta x, \delta y, \delta z, …$であり，それぞれの測定誤差に相関が無い時，関数$f(x, y, z, …)$の誤差$\delta f$は次のようになる．
$$\delta f = \sqrt{\left(\frac{\partial f}{\partial x}\delta x\right)^2 + \left(\frac{\partial f}{\partial y}\delta y\right)^2 + \left(\frac{\partial f}{\partial z}\delta z\right)^2 + …}$$

よって，パラメータの誤差の相関が0である場合，積分強度の誤差は次のように求まります．

$$\delta I = \sqrt{\left(\sigma\sqrt{2\pi}\delta A\right)^2 + \left(A\sqrt{2\pi}\delta \sigma \right)^2 }$$

# 積分強度の誤差
d_I = ((sigma * (2 * math.pi) ** 0.5 * d_A) ** 2 + ((A * (2 * math.pi) ** 0.5 * d_sigma))) ** 0.5

また，$I = A\sigma \cdot \sqrt{2\pi}$のように，積分強度を$A\sigma$の定数（$ \sqrt{2\pi}$）倍とみれば，$\delta I$をより簡潔に求めることもできます．

$$\delta I = \sqrt{(\sigma\delta A)^2 + (A\delta \sigma)^2 } \sqrt{2\pi}$$

さいごに

本記事では正規分布を取るデータを例に，その解析方法について解説しました．フィッティングによって求まった各パラメータとそれらの誤差を基に，各種の物理量などの誤差を算出するためには，誤差解析の理解が必要です．本記事で紹介した

任意の1次変数関数における誤差
任意の多変数関数における誤差

など，詳しく載っている書籍を紹介します．こちらの本は，学部時代に天文学系の研究室でデータ解析を行っていた際に，指導教員の方に紹介してもらったものです．欲しい情報を的確に得られると感じたので，おすすめの１冊です．

参考：「計測における誤差解析入門」JOHN R. TAYLOR 著，林茂雄・馬場凉訳