【静電エネルギー】2. ２つの点電荷の静電エネルギーを導出する

２つの点電荷\(q_1, q_2\)をそれぞれ無限遠から, \(\mathbf{r}_1, \mathbf{r}_2\)に運ぶために要する仕事は,
$$U = \frac{1}{4\pi\varepsilon_0}\frac{q_1 q_2}{|\mathbf{r}_1 – \mathbf{r}_2|}$$
で与えられ, これを点電荷\(q_1, q_2\)の持つ静電エネルギーと呼ぶ.

これを示してみよう.

（１）2つの点電荷が無限遠にある始状態

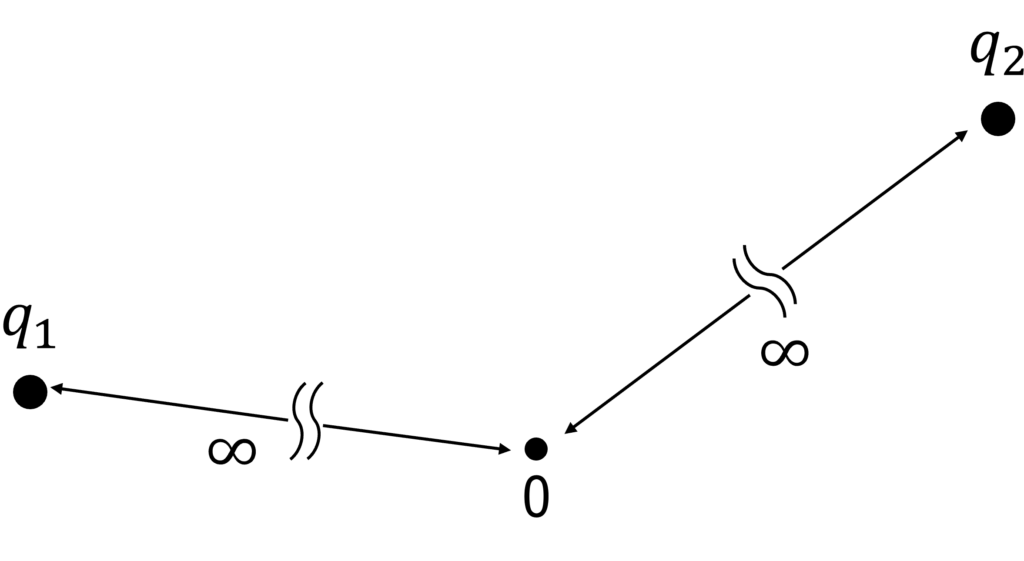
はじめ, 点電荷\(q_1, q_2\)は互いに無限に遠く離れているとする. また, ２つの点電荷は, 原点Oからも無限遠にあるとする.

（２）１つ目の点電荷を運んでくる

最初, 電荷\(q_1\)を位置\(\mathbf{r}_1\)まで運ぶときは, 電荷に力が働かないので, 要する仕事は0である.

（３）２つ目の点電荷を運んでくる

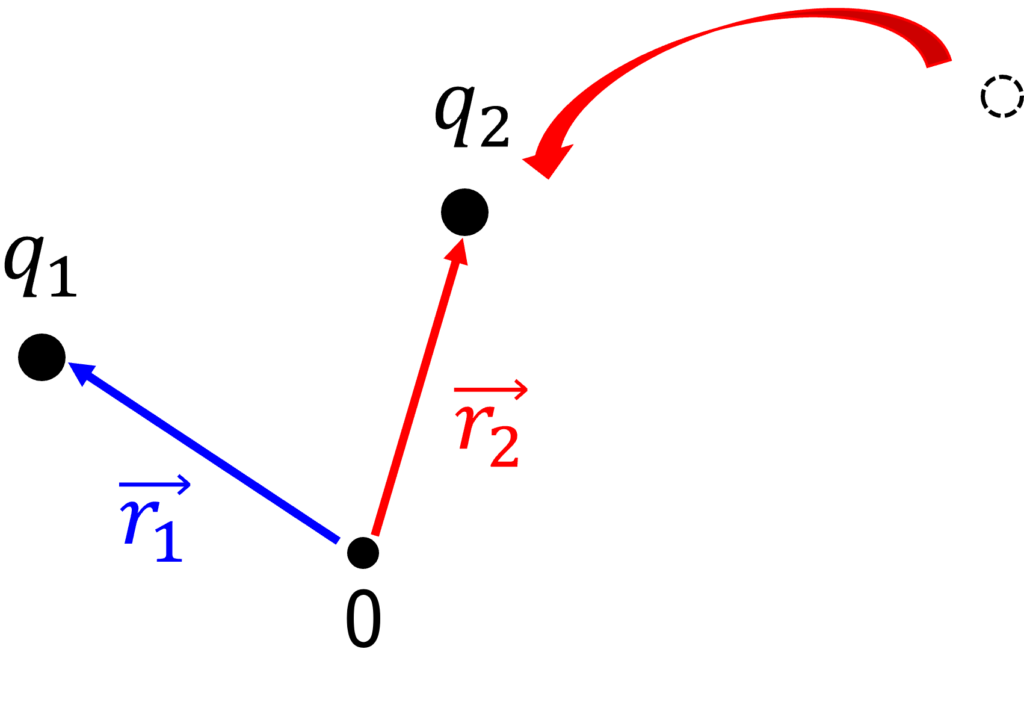
次に, 電荷\(q_2\)を位置\(\mathbf{r}_2\)まで運ぶときは, 電荷\(q_2\)を電荷\(q_1\)のつくる電場

$$\mathbf{E}_1 = \frac{q_1}{4\pi\varepsilon_0}\frac{\mathbf{r} – \mathbf{r}_1}{|\mathbf{r} – \mathbf{r}_1|}$$

の中で動かすことになるので, 要する仕事は0ではない. ここで,

で解説しているように,

点Oを基準としたとき, 点Pに存在する電荷\(q\)の静電エネルギー
\begin{align*}
U_\mathrm{P} &= q\phi\\
&= q(\phi (\mathrm{P}) – \phi (\mathrm{O}))
\end{align*}
ただし, \(\phi\)は, 考えている空間上の電位を表す.

を用いる. 今, は点電荷\(q_1\)の作る電位\(\phi_1 (\mathbf{r})\)中で, 点電荷\(q_2\)を動かしていることに注意する. すると, 今基準点を\(\infty\)で表すとすれば, 必要な仕事として次が得られる.

\begin{align*}
U &= q\phi_\mathrm{P}\\
&= q_2 \phi _1(\mathbf{r}_2) – \phi _1(\infty)\\
&= \frac{q_1q_2}{4\pi\varepsilon_0}\frac{\mathbf{r}_2 – \mathbf{r}_1}{|\mathbf{r}_2 – \mathbf{r}_1|}
\end{align*}

したがって,

位置\(\mathbf{r}_1, \mathbf{r}_2\)に存在する２つの点電荷\(q_1, q_2\)の持つ静電エネルギー:
$$U = \frac{q_1q_2}{4\pi\varepsilon_0}\frac{\mathbf{r}_2 – \mathbf{r}_1}{|\mathbf{r} – \mathbf{r}_1|}$$

を導くことができた.