電荷\(Q\)が半径\(R\)の球の内部に一様に分布しているときの, 静電エネルギーを求めよ.
[解]
1. 無限遠から球殻状の電荷を運ぶ
無限遠から原点の周りに電荷を運び, 一様な密度\(\rho = \frac{Q}{4/3 \pi R^3}\)で分布させながら, 球を徐々に大きくしていく.
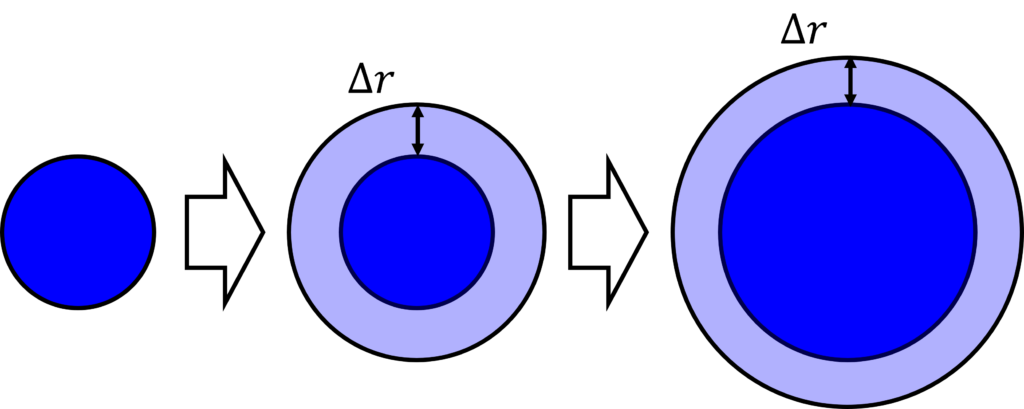
まず, 半径\(r , (< R)\)の球ができた状態で, さらに電荷を運んで, 半径を\(\Delta r\)だけ大きくするために必要な仕事\(\Delta W\)を求める. 半径\(r\)の球と, 半径\(r + \Delta r\)の球に挟まれた, 微小な厚み\(\Delta r\)をもつ球殻の体積は, \(\Delta r\)が十分に小さいとき,
$$\Delta V = 4\pi r^2 \cdot \Delta r$$
と表すことができる.
※\(\Delta r\)が十分に小さければ, 球殻の内側の球と, 外側の球の表面積は共に\(4\pi r^2\)でほぼ等しい.
したがって, 運ぶ電荷の量は
\begin{align*}
\Delta Q &= \Delta V\cdot \rho \\
&= 4\pi r^2\Delta r\rho
\end{align*}
2. 球殻状の電荷を運ぶのに必要な仕事
球内に一様に分布した電荷の作る電場は,
で求めたように, 球の外では, 全電荷が球の中心に(点電荷として)存在するのと同じになる. したがって, 球の外であれば, ポテンシャルも球の中心にある点電荷によるものと同じだと考えることができる.
なお, 点電荷による電位は次の記事で解説している.
すると, 半径\(r\)の球面上における電位は,
\begin{align*}
\phi_{surf} &= \frac{1}{4\pi\varepsilon_0 r}\cdot \frac{4}{3}\pi r^3 \rho \\
&= \frac{\rho r^2}{3\varepsilon_0}
\end{align*}
となる. これに, 運ぶべき電荷の量\(\Delta Q\)をかけたものが, 無限遠から半径\(r\)の球面上まで電荷を運ぶのに必要な仕事\(\Delta W\)になる.
\begin{align*}
\Delta W &= phi_{surf}\cdot \Delta Q\\
&= \frac{4pi\rho^2}{3\varepsilon_0}r^4\Delta r
\end{align*}
3. 静電エネルギーを求める
ここで, 冒頭で述べたように, 球殻を次々に運んでくることを考える. 必要な仕事の総和\(\sum \Delta W\)は, \(\Delta r \rightarrow 0\)の極限を取ると, \(r\)について\(r = 0\)から\(r = R\)までの積分になり, これは求めるべき静電エネルギー\(U)に等しい.
\begin{align*}
U &= \int \Delta W\\
&= \frac{4pi\rho^2}{3\varepsilon_0}\int_0^R r^4 dr\\
&= \frac{4pi\rho^2}{15\varepsilon_0}R^5\\
&= \frac{3Q^2}{20\pi\varepsilon_0 R}
\end{align*}
最後の式変形では, 密度と総電荷の関係\(\rho = \frac{Q}{4/3 \pi R^3}\)を用いた.
さいごに
半径\(r\)の球が初めから存在するかのように議論を進めてきたが, \(r\)がほぼ0のとき, すなわち点電荷とみなせるくらい広がりの小さい最初の電荷を, 所定の位置まで要する仕事は0である. よって, 上記で考えた球殻の積分についての議論は成り立つ.
参考:物理入門コース「例解 電磁気学演習」 長岡洋介・丹慶勝市





コメント