半径\(r\)の球面Sがある. 中心から\(r\)の距離にある点Aに置かれた点電荷\(q\)が, 球面S上の点に作る電場\(\mathbf{E}(\mathbf{r})\)について, 面積分\(\int_S\left\{\mathbf{E}(\mathbf{r})\cdot\mathbf{n(\mathbf{r})}\right\}\mathrm{d}S\)を計算し, \(r \ne R\)のとき, ガウスの法則が成り立つことを確かめよ. また, \(r = R\)ではどうか.
[解]
球の中心を原点Oとし, 点Aを通るようにz軸をとり, 図のように球面上の点Pを\(R, \theta, \varphi\)によって定める.
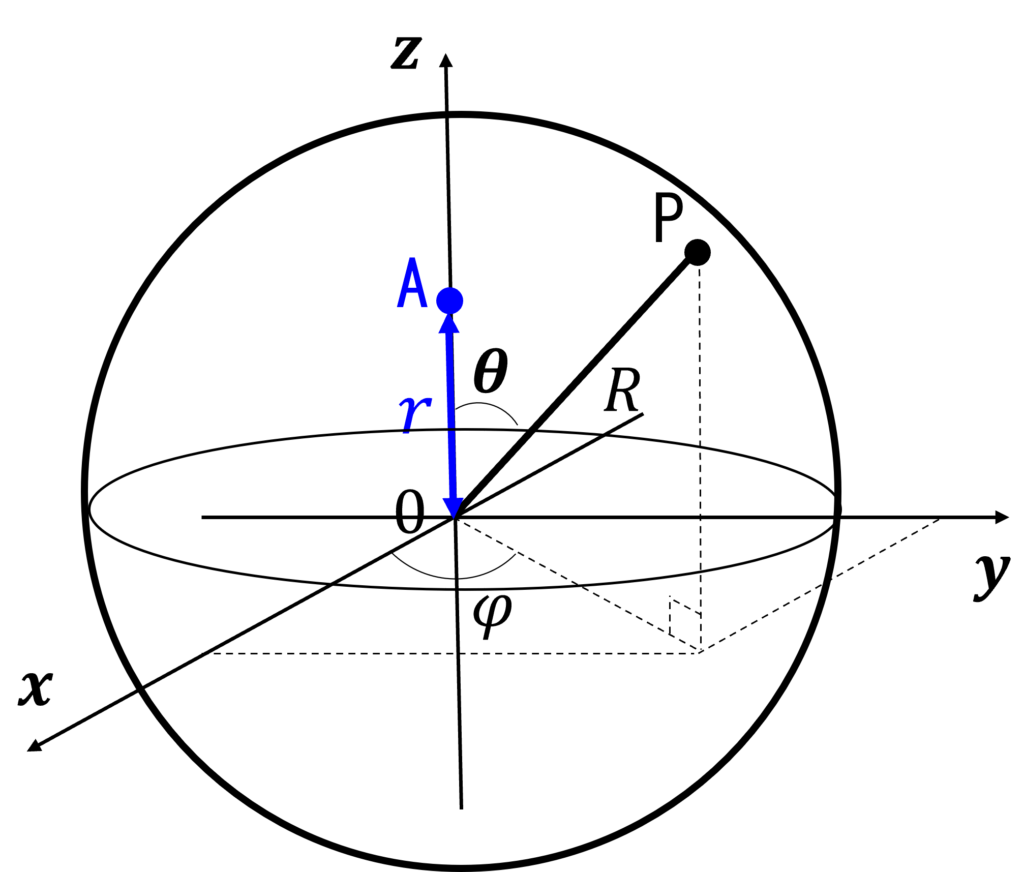
余弦定理により, AP間の距離を求めると,
$$\mathrm{AP}^2 = r^2 + R^2 – 2rRcos\theta$$
また, 下図のように, \(\vec{AP}\)と点Pにおける球面上の法線ベクトル\(\mathbf{n}\)とがなす角\(\alpha\)とすると,
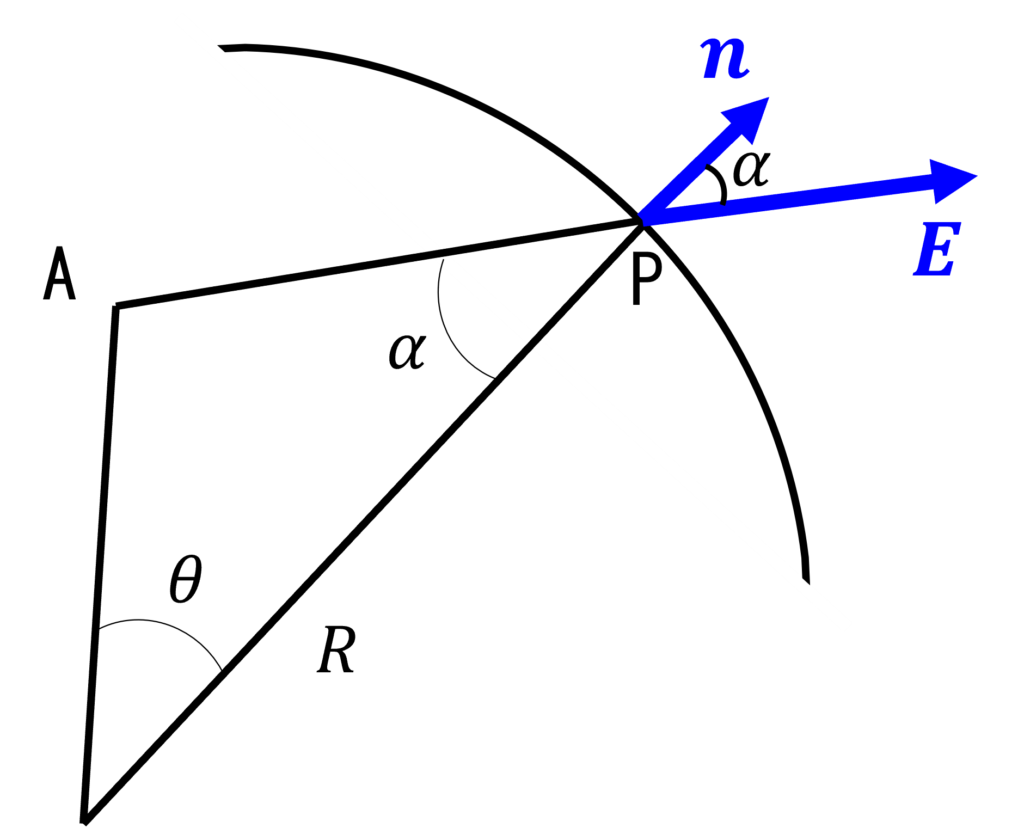
$$\mathbf{E}(\mathrm{r})\cdot\mathbf{n}(\mathrm{r}) = |\mathbf{E}|\mathrm{cos}\alpha$$
であるから, \(\mathrm{cos}\alpha\)を余弦定理によって求めると,
\begin{align*}
\mathrm{cos}\alpha &= \frac{\mathrm{AP}^2 + \mathrm{OP}^2 – \mathrm{OA}^2}{2OA\cdot OP}\\
&= \frac{(r^2 + R^2 – 2rR\mathrm{cos}\theta) + R^2 – r^2}{2\sqrt{r^2 + R^2 – 2rR\mathrm{cos}\theta}\cdot R}\\
&= \frac{R – r\mathrm{cos}\theta}{\sqrt{r^2 + R^2 – 2rR\mathrm{cos}\theta}}
\end{align*}
ここで, 点Pにおける面要素は
$$\mathrm{d}S = R^2\mathrm{sin}\theta \mathrm{d}\theta \mathrm{d}\varphi$$
である.
したがって,
\begin{align*}
\int_S\mathbf{E}(\mathbf{r})\cdot\mathbf{n(\mathbf{r})}\mathrm{d}S &= \int_S\frac{q}{4\pi\varepsilon_0}\frac{1}{\mathrm{AP}^2}\mathrm{cos}\alpha\mathrm{d}S\\
&= \frac{q}{4\pi\varepsilon_0}\int_S\frac{R – r\mathrm{cos}\theta}{(r^2 + R^2 – 2rR\mathrm{cos}\theta)^{3/2}}\cdot R^2\mathrm{sin}\theta \mathrm{d}\theta \mathrm{d}\varphi\\
&= \frac{qR^2}{4\pi\varepsilon_0}\int_{\varphi = 0}^{\varphi =2\pi}\int_{\theta = 0}^{\theta =\pi}\frac{R – r\mathrm{cos}\theta}{(r^2 + R^2 – 2rR\mathrm{cos}\theta)^{3/2}} \mathrm{d}\theta \mathrm{d}\varphi\\
&= \frac{qR^2}{4\pi\varepsilon_0}\cdot 2\pi\int_{\theta = 0}^{\theta =\pi}\frac{R – r\mathrm{cos}\theta}{(r^2 + R^2 – 2rR\mathrm{cos}\theta)^{3/2}} \mathrm{d}\theta \mathrm{d}\varphi \ …(1)\\
&= \frac{qR^2}{2\varepsilon_0}\int_1^{-1}\frac{R – rt}{(r^2 + R^2 – 2rRt)^{3/2}}(-\mathrm{d}t) \ …(2)\\
&= \frac{qR}{4\varepsilon_0}\int_{-1}^1\frac{2R^2 – 2rRt}{(r^2 + R^2 – 2rRt)^{3/2}}\mathrm{d}t\\
&= \frac{qR}{4\varepsilon_0}\int_{-1}^1\frac{R^2 – 2rRt + r^2 + (-r^2 + R^2)}{(r^2 + R^2 – 2rRt)^{3/2}}\mathrm{d}t\\
&= \frac{qR}{4\varepsilon_0}\left[-\frac{1}{rR}\left(r^2 + R^2 -2rRt\right)^{1/2} + \frac{R^2 – r^2}{rR}\left(r^2 + R^2 -2rRt\right)^{-1/2}\right]_{-1}^1\\
&= \frac{q}{4\varepsilon_0 r}\left[-\left((r – R)^2\right)^{1/2} + \left((r + R)^2\right)^{1/2} + (R^2 – r^2)\left\{\left((r – R)^2\right)^{-1/2} – \left((r + R)^2\right)^{-1/2}\right\}\right]
\end{align*}
(1)では, \(\varphi\)についての積分を行った.
(2)では, \(t = \mathrm{cos}\theta\)と置換し, \(\mathrm{d}t = – \mathrm{sin}\theta\mathrm{d}\theta\)となることを用いた.
以上の結果を絶対値を用いて整理すると, 次のように書くことができる.
\begin{align*}
&\int_S\mathbf{E}(\mathbf{r})\cdot\mathbf{n(\mathbf{r})}\mathrm{d}S\\
& \ = \frac{q}{4\varepsilon_0}\left\{-|r-R| + (r + R) + (R^2 – r^2)\cdot \frac{1}{|r – R|} – (R^2 – r^2)\frac{1}{r + R}\right\} \ …(3)
\end{align*}
ゆえに
\(r > R\)の場合(球面の外に点電荷がある時), (3)の計算結果は
$$\int_S\mathbf{E}(\mathbf{r})\cdot\mathbf{n(\mathbf{r})}\mathrm{d}S = 0$$
となる.
\(r < R\)の場合(球面の内側に点電荷がある時), (3)は
$$\int_S\mathbf{E}(\mathbf{r})\cdot\mathbf{n(\mathbf{r})}\mathrm{d}S = \frac{q}{\varepsilon_0}$$
となる.
以上の結果より,
「任意の平曲面に囲まれた電荷の総量(を誘電率で割った値)は, 平曲面上における電場の面積積分の値に一致する」というガウスの法則が成り立っている. すなわち, \(r > R\)の時は球面内に電荷が存在しないため, 積分値は0となり, \(r < R\)の時は, 球面内に電荷が収まっているので, 積分値は電荷を誘電率で割った値に一致する.
最後に, \(r = R\)の場合を考える.
\begin{align*}
\int_S\mathbf{E}(\mathbf{r})\cdot\mathbf{n(\mathbf{r})}\mathrm{d}S = \frac{qR^2}{4\pi\varepsilon_0}\cdot 2\pi\int_{\theta = 0}^{\theta =\pi}\frac{R – r\mathrm{cos}\theta}{(r^2 + R^2 – 2rR\mathrm{cos}\theta)^{3/2}} \mathrm{d}\theta \mathrm{d}\varphi \ …(1) \\
&= \frac{q}{4\sqrt{2}\varepsilon_0}\int_0^{\pi}\frac{\mathrm{sin}\theta}{\sqrt{1 – \mathrm{cos}\theta}}\mathrm{d}\theta\\
&= \frac{q}{4\sqrt{2}\varepsilon_0}\left[2\sqrt{1 – \mathrm{cos}\theta}\right]_0^{\pi}\\
&= \frac{q}{2\varepsilon_0}
\end{align*}
これは, 電荷の半分は球面内に収まっており, もう半分は球面外に存在すると解釈することができる.



コメント